JEE Exam > JEE Questions > The locus of the point of intersection of the...
Start Learning for Free
The locus of the point of intersection of the lines, √2 x – y + 4 √2 k = 0 and √2 kx + ky – 4 √2 = 0 (k is any non-zero real parameter), is
- a)an ellipse whose eccentricity is 1/√3
- b)a hyperbola whose eccentricity is √3
- c)a hyperbola with length of its transverse axis 8√2
- d)an ellipse with length of its major axis 8√2
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The locus of the point of intersection of the lines, √2 x &ndash...
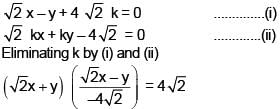
Most Upvoted Answer
The locus of the point of intersection of the lines, √2 x &ndash...
Understanding the Locus of Intersection Points
The problem involves finding the locus of intersection points of two lines influenced by a parameter 'k'. Let's analyze the equations given:
1. Line Equations:
- Line 1: √2x - y + 4√2k = 0
- Line 2: √2kx + ky - 4√2 = 0
2. Finding Intersection:
- To find the intersection, we solve these equations simultaneously. We can express 'y' from Line 1 and substitute it into Line 2.
Substituting and Rearranging
- From Line 1, we can express y as:
y = √2x + 4√2k
- Substitute this in Line 2:
√2kx + k(√2x + 4√2k) - 4√2 = 0
- This simplifies to:
(√2k + k√2)x + 4k^2 - 4√2 = 0
(2√2k)x + 4k^2 - 4√2 = 0
Resulting Equation
- From the above, rearranging gives us a quadratic in 'x' based on 'k', leading to:
x = (2√2 - 4k^2)/(2√2k)
Identifying the Locus
- As 'k' varies, the above expression describes a hyperbola. The key points here are:
- The hyperbola's transverse axis length and the eccentricity can be derived from the standard form.
- The transverse axis length is found to be 8√2.
Conclusion
Thus, the locus of the intersection points forms a hyperbola with a transverse axis length of 8√2. Hence, the correct answer is option 'C'.
The problem involves finding the locus of intersection points of two lines influenced by a parameter 'k'. Let's analyze the equations given:
1. Line Equations:
- Line 1: √2x - y + 4√2k = 0
- Line 2: √2kx + ky - 4√2 = 0
2. Finding Intersection:
- To find the intersection, we solve these equations simultaneously. We can express 'y' from Line 1 and substitute it into Line 2.
Substituting and Rearranging
- From Line 1, we can express y as:
y = √2x + 4√2k
- Substitute this in Line 2:
√2kx + k(√2x + 4√2k) - 4√2 = 0
- This simplifies to:
(√2k + k√2)x + 4k^2 - 4√2 = 0
(2√2k)x + 4k^2 - 4√2 = 0
Resulting Equation
- From the above, rearranging gives us a quadratic in 'x' based on 'k', leading to:
x = (2√2 - 4k^2)/(2√2k)
Identifying the Locus
- As 'k' varies, the above expression describes a hyperbola. The key points here are:
- The hyperbola's transverse axis length and the eccentricity can be derived from the standard form.
- The transverse axis length is found to be 8√2.
Conclusion
Thus, the locus of the intersection points forms a hyperbola with a transverse axis length of 8√2. Hence, the correct answer is option 'C'.
Attention JEE Students!
To make sure you are not studying endlessly, EduRev has designed JEE study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in JEE.
|
Explore Courses for JEE exam
|
|
Similar JEE Doubts
Top Courses for JEEView all
The locus of the point of intersection of the lines, √2 x – y + 4 √2 k= 0 and √2 kx + ky – 4 √2 = 0(k is any non-zero real parameter), isa)an ellipse whose eccentricity is 1/√3b)a hyperbola whose eccentricity is √3c)a hyperbola with length of its transverse axis 8√2d)an ellipse with length of its major axis 8√2Correct answer is option 'C'. Can you explain this answer?
Question Description
The locus of the point of intersection of the lines, √2 x – y + 4 √2 k= 0 and √2 kx + ky – 4 √2 = 0(k is any non-zero real parameter), isa)an ellipse whose eccentricity is 1/√3b)a hyperbola whose eccentricity is √3c)a hyperbola with length of its transverse axis 8√2d)an ellipse with length of its major axis 8√2Correct answer is option 'C'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about The locus of the point of intersection of the lines, √2 x – y + 4 √2 k= 0 and √2 kx + ky – 4 √2 = 0(k is any non-zero real parameter), isa)an ellipse whose eccentricity is 1/√3b)a hyperbola whose eccentricity is √3c)a hyperbola with length of its transverse axis 8√2d)an ellipse with length of its major axis 8√2Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The locus of the point of intersection of the lines, √2 x – y + 4 √2 k= 0 and √2 kx + ky – 4 √2 = 0(k is any non-zero real parameter), isa)an ellipse whose eccentricity is 1/√3b)a hyperbola whose eccentricity is √3c)a hyperbola with length of its transverse axis 8√2d)an ellipse with length of its major axis 8√2Correct answer is option 'C'. Can you explain this answer?.
The locus of the point of intersection of the lines, √2 x – y + 4 √2 k= 0 and √2 kx + ky – 4 √2 = 0(k is any non-zero real parameter), isa)an ellipse whose eccentricity is 1/√3b)a hyperbola whose eccentricity is √3c)a hyperbola with length of its transverse axis 8√2d)an ellipse with length of its major axis 8√2Correct answer is option 'C'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about The locus of the point of intersection of the lines, √2 x – y + 4 √2 k= 0 and √2 kx + ky – 4 √2 = 0(k is any non-zero real parameter), isa)an ellipse whose eccentricity is 1/√3b)a hyperbola whose eccentricity is √3c)a hyperbola with length of its transverse axis 8√2d)an ellipse with length of its major axis 8√2Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The locus of the point of intersection of the lines, √2 x – y + 4 √2 k= 0 and √2 kx + ky – 4 √2 = 0(k is any non-zero real parameter), isa)an ellipse whose eccentricity is 1/√3b)a hyperbola whose eccentricity is √3c)a hyperbola with length of its transverse axis 8√2d)an ellipse with length of its major axis 8√2Correct answer is option 'C'. Can you explain this answer?.
Solutions for The locus of the point of intersection of the lines, √2 x – y + 4 √2 k= 0 and √2 kx + ky – 4 √2 = 0(k is any non-zero real parameter), isa)an ellipse whose eccentricity is 1/√3b)a hyperbola whose eccentricity is √3c)a hyperbola with length of its transverse axis 8√2d)an ellipse with length of its major axis 8√2Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of The locus of the point of intersection of the lines, √2 x – y + 4 √2 k= 0 and √2 kx + ky – 4 √2 = 0(k is any non-zero real parameter), isa)an ellipse whose eccentricity is 1/√3b)a hyperbola whose eccentricity is √3c)a hyperbola with length of its transverse axis 8√2d)an ellipse with length of its major axis 8√2Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The locus of the point of intersection of the lines, √2 x – y + 4 √2 k= 0 and √2 kx + ky – 4 √2 = 0(k is any non-zero real parameter), isa)an ellipse whose eccentricity is 1/√3b)a hyperbola whose eccentricity is √3c)a hyperbola with length of its transverse axis 8√2d)an ellipse with length of its major axis 8√2Correct answer is option 'C'. Can you explain this answer?, a detailed solution for The locus of the point of intersection of the lines, √2 x – y + 4 √2 k= 0 and √2 kx + ky – 4 √2 = 0(k is any non-zero real parameter), isa)an ellipse whose eccentricity is 1/√3b)a hyperbola whose eccentricity is √3c)a hyperbola with length of its transverse axis 8√2d)an ellipse with length of its major axis 8√2Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of The locus of the point of intersection of the lines, √2 x – y + 4 √2 k= 0 and √2 kx + ky – 4 √2 = 0(k is any non-zero real parameter), isa)an ellipse whose eccentricity is 1/√3b)a hyperbola whose eccentricity is √3c)a hyperbola with length of its transverse axis 8√2d)an ellipse with length of its major axis 8√2Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The locus of the point of intersection of the lines, √2 x – y + 4 √2 k= 0 and √2 kx + ky – 4 √2 = 0(k is any non-zero real parameter), isa)an ellipse whose eccentricity is 1/√3b)a hyperbola whose eccentricity is √3c)a hyperbola with length of its transverse axis 8√2d)an ellipse with length of its major axis 8√2Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice JEE tests.
|
|
Explore Courses for JEE exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup