IIT JAM Exam > IIT JAM Questions > In the gas phase, the ratio of excluded volum...
Start Learning for Free
In the gas phase, the ratio of excluded volume to molecular volume for a spherical molecule is _______
Correct answer is '8'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
In the gas phase, the ratio of excluded volume to molecular volume for...
First, one recognizes that molecules take up space so that the volume occupied by the gas is only party-free space. It seems reasonable to replace V in the ideal gas law by the free space volume V - b where b is the effective volume occupied by a mole of molecules. This volume b is not the actual molar volume but is so-called excluded volume.The point involved in the illustrated figure, in this case, two identical spherical molecules the center of an approaching molecule. A cannot come closer than the distance 2r ( r being the radius) to the center of another like molecule B thus the excluded volume is
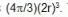 The effect of the effect is a mutual one so the ratio is excluded volume of molecular space of a spherical molecule is
The effect of the effect is a mutual one so the ratio is excluded volume of molecular space of a spherical molecule is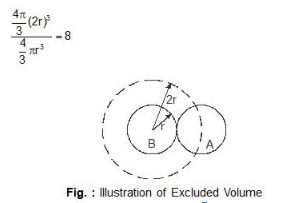
Most Upvoted Answer
In the gas phase, the ratio of excluded volume to molecular volume for...
Ratio of excluded volume to molecular volume:
In the gas phase, the ratio of excluded volume to molecular volume for a spherical molecule is 8. This means that the excluded volume, which refers to the space that is unavailable for other molecules due to the presence of a molecule, is eight times larger than the molecular volume of the molecule itself.
Explanation:
When considering the gas phase, molecules are assumed to be in constant motion and have negligible interactions with each other, except for brief collisions. In this scenario, the size and shape of the molecules become important factors in determining their behavior.
Molecular volume:
The molecular volume of a spherical molecule refers to the actual physical space occupied by the molecule. It is calculated based on the molecular dimensions and can be visualized as a sphere with a certain radius.
Excluded volume:
The excluded volume, on the other hand, takes into account the repulsive forces between molecules that prevent them from occupying the same space simultaneously. It represents the additional space required around a molecule to prevent overlap with other molecules.
Ratio of excluded volume to molecular volume:
The ratio of excluded volume to molecular volume is a measure of the relative size of the space that a molecule effectively occupies compared to the space it physically occupies. In the case of a spherical molecule, this ratio is 8.
Derivation:
To understand why the ratio is 8, we can consider a simplified model where molecules are treated as hard spheres with no attractive forces. In this model, the excluded volume can be approximated using the Van der Waals equation of state.
The Van der Waals equation takes into account the size of the molecules by introducing a correction term, called the excluded volume term. This term represents the space that is excluded or unavailable for other molecules due to the presence of a molecule.
For a spherical molecule, the excluded volume term can be calculated using the formula: V_ex = 4/3 * π * (r + b)^3, where r is the radius of the molecule and b is the excluded volume correction parameter.
Comparing this with the molecular volume formula V_mol = 4/3 * π * r^3, we can calculate the ratio of excluded volume to molecular volume:
Ratio = V_ex / V_mol = (4/3 * π * (r + b)^3) / (4/3 * π * r^3)
= (r + b)^3 / r^3
Assuming that the molecule is spherical and has a radius of r, we can simplify the equation further:
Ratio = (r + b)^3 / r^3
= (r/r)^3 + 3 * (r/r)^2 * (b/r) + 3 * (r/r) * (b/r)^2 + (b/r)^3
= 1 + 3 * (b/r) + 3 * (b/r)^2 + (b/r)^3
In the limit of small values of b/r, where the excluded volume is much larger than the molecular volume, the higher-order terms become negligible, and the ratio simplifies to:
Ratio ≈ 1 + 3 * (b/r)
Since the ratio is given as 8, we can solve the equation:
8 = 1 + 3 * (b/r)
3 * (b/r)
In the gas phase, the ratio of excluded volume to molecular volume for a spherical molecule is 8. This means that the excluded volume, which refers to the space that is unavailable for other molecules due to the presence of a molecule, is eight times larger than the molecular volume of the molecule itself.
Explanation:
When considering the gas phase, molecules are assumed to be in constant motion and have negligible interactions with each other, except for brief collisions. In this scenario, the size and shape of the molecules become important factors in determining their behavior.
Molecular volume:
The molecular volume of a spherical molecule refers to the actual physical space occupied by the molecule. It is calculated based on the molecular dimensions and can be visualized as a sphere with a certain radius.
Excluded volume:
The excluded volume, on the other hand, takes into account the repulsive forces between molecules that prevent them from occupying the same space simultaneously. It represents the additional space required around a molecule to prevent overlap with other molecules.
Ratio of excluded volume to molecular volume:
The ratio of excluded volume to molecular volume is a measure of the relative size of the space that a molecule effectively occupies compared to the space it physically occupies. In the case of a spherical molecule, this ratio is 8.
Derivation:
To understand why the ratio is 8, we can consider a simplified model where molecules are treated as hard spheres with no attractive forces. In this model, the excluded volume can be approximated using the Van der Waals equation of state.
The Van der Waals equation takes into account the size of the molecules by introducing a correction term, called the excluded volume term. This term represents the space that is excluded or unavailable for other molecules due to the presence of a molecule.
For a spherical molecule, the excluded volume term can be calculated using the formula: V_ex = 4/3 * π * (r + b)^3, where r is the radius of the molecule and b is the excluded volume correction parameter.
Comparing this with the molecular volume formula V_mol = 4/3 * π * r^3, we can calculate the ratio of excluded volume to molecular volume:
Ratio = V_ex / V_mol = (4/3 * π * (r + b)^3) / (4/3 * π * r^3)
= (r + b)^3 / r^3
Assuming that the molecule is spherical and has a radius of r, we can simplify the equation further:
Ratio = (r + b)^3 / r^3
= (r/r)^3 + 3 * (r/r)^2 * (b/r) + 3 * (r/r) * (b/r)^2 + (b/r)^3
= 1 + 3 * (b/r) + 3 * (b/r)^2 + (b/r)^3
In the limit of small values of b/r, where the excluded volume is much larger than the molecular volume, the higher-order terms become negligible, and the ratio simplifies to:
Ratio ≈ 1 + 3 * (b/r)
Since the ratio is given as 8, we can solve the equation:
8 = 1 + 3 * (b/r)
3 * (b/r)

|
Explore Courses for IIT JAM exam
|

|
Similar IIT JAM Doubts
In the gas phase, the ratio of excluded volume to molecular volume for a spherical molecule is _______Correct answer is '8'. Can you explain this answer?
Question Description
In the gas phase, the ratio of excluded volume to molecular volume for a spherical molecule is _______Correct answer is '8'. Can you explain this answer? for IIT JAM 2024 is part of IIT JAM preparation. The Question and answers have been prepared according to the IIT JAM exam syllabus. Information about In the gas phase, the ratio of excluded volume to molecular volume for a spherical molecule is _______Correct answer is '8'. Can you explain this answer? covers all topics & solutions for IIT JAM 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In the gas phase, the ratio of excluded volume to molecular volume for a spherical molecule is _______Correct answer is '8'. Can you explain this answer?.
In the gas phase, the ratio of excluded volume to molecular volume for a spherical molecule is _______Correct answer is '8'. Can you explain this answer? for IIT JAM 2024 is part of IIT JAM preparation. The Question and answers have been prepared according to the IIT JAM exam syllabus. Information about In the gas phase, the ratio of excluded volume to molecular volume for a spherical molecule is _______Correct answer is '8'. Can you explain this answer? covers all topics & solutions for IIT JAM 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In the gas phase, the ratio of excluded volume to molecular volume for a spherical molecule is _______Correct answer is '8'. Can you explain this answer?.
Solutions for In the gas phase, the ratio of excluded volume to molecular volume for a spherical molecule is _______Correct answer is '8'. Can you explain this answer? in English & in Hindi are available as part of our courses for IIT JAM.
Download more important topics, notes, lectures and mock test series for IIT JAM Exam by signing up for free.
Here you can find the meaning of In the gas phase, the ratio of excluded volume to molecular volume for a spherical molecule is _______Correct answer is '8'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
In the gas phase, the ratio of excluded volume to molecular volume for a spherical molecule is _______Correct answer is '8'. Can you explain this answer?, a detailed solution for In the gas phase, the ratio of excluded volume to molecular volume for a spherical molecule is _______Correct answer is '8'. Can you explain this answer? has been provided alongside types of In the gas phase, the ratio of excluded volume to molecular volume for a spherical molecule is _______Correct answer is '8'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice In the gas phase, the ratio of excluded volume to molecular volume for a spherical molecule is _______Correct answer is '8'. Can you explain this answer? tests, examples and also practice IIT JAM tests.

|
Explore Courses for IIT JAM exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















