Physics Exam > Physics Questions > The energy of an electron moving in one dimen...
Start Learning for Free
The energy of an electron moving in one dimension in an infinitely high potential box of width 1Å.
Correct answer is '37.62'. Can you explain this answer?
Most Upvoted Answer
The energy of an electron moving in one dimension in an infinitely hig...
The eigenvalue of energy
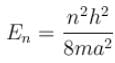
when the particle is in the least energy state (n = 1), the energy
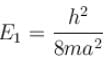 with h = 6.62 × 10–34 Js, m = 9.1 × 10–31 kg and a = 1 × 10–10 m
with h = 6.62 × 10–34 Js, m = 9.1 × 10–31 kg and a = 1 × 10–10 mAfter calculating,
The correct answer is: 37.62 eV
Free Test
FREE
| Start Free Test |
Community Answer
The energy of an electron moving in one dimension in an infinitely hig...
To find the energy of an electron in a one-dimensional infinitely high potential box of width 1, we can use the Schrödinger equation for a particle in a box. The Schrödinger equation for a particle in a one-dimensional box is given by:
-((ħ^2)/(2m)) * (∂^2ψ/∂x^2) + V(x)ψ = Eψ
In this case, the potential energy inside the box is zero, and outside the box it is infinitely high. Therefore, the potential energy function V(x) is:
V(x) = {
0, 0 ≤ x ≤ 1
∞, x < 0="" or="" x="" /> 1
}
Since the potential energy is zero inside the box, the Schrödinger equation simplifies to:
-((ħ^2)/(2m)) * (∂^2ψ/∂x^2) = Eψ
We can solve this second-order differential equation to find the possible energy levels of the electron. The general solution to this equation will be a combination of sine and cosine functions. However, since the potential energy is infinitely high outside the box, the wavefunction must be zero at x = 0 and x = 1.
Therefore, the boundary conditions for the wavefunction are:
ψ(0) = 0
ψ(1) = 0
Using these boundary conditions, we can find the allowed energy levels by solving the equation -((ħ^2)/(2m)) * (∂^2ψ/∂x^2) = Eψ subject to the boundary conditions.
The solutions to this equation will give us the energy eigenvalues for the electron in the box. The energy levels will be quantized, meaning they will take on discrete values. The lowest energy level (the ground state) will have the lowest energy, and the energy levels will increase as we move to higher energy states.
To find the specific energy values, we need to solve the differential equation and apply the boundary conditions. The solutions will be in the form of a wavefunction ψ(x), and the corresponding energy levels E will be determined by the solutions.
Note: The specific solutions and energy levels will depend on the chosen unit system, such as the units used for the Planck constant (ħ) and the mass of the electron (m).
-((ħ^2)/(2m)) * (∂^2ψ/∂x^2) + V(x)ψ = Eψ
In this case, the potential energy inside the box is zero, and outside the box it is infinitely high. Therefore, the potential energy function V(x) is:
V(x) = {
0, 0 ≤ x ≤ 1
∞, x < 0="" or="" x="" /> 1
}
Since the potential energy is zero inside the box, the Schrödinger equation simplifies to:
-((ħ^2)/(2m)) * (∂^2ψ/∂x^2) = Eψ
We can solve this second-order differential equation to find the possible energy levels of the electron. The general solution to this equation will be a combination of sine and cosine functions. However, since the potential energy is infinitely high outside the box, the wavefunction must be zero at x = 0 and x = 1.
Therefore, the boundary conditions for the wavefunction are:
ψ(0) = 0
ψ(1) = 0
Using these boundary conditions, we can find the allowed energy levels by solving the equation -((ħ^2)/(2m)) * (∂^2ψ/∂x^2) = Eψ subject to the boundary conditions.
The solutions to this equation will give us the energy eigenvalues for the electron in the box. The energy levels will be quantized, meaning they will take on discrete values. The lowest energy level (the ground state) will have the lowest energy, and the energy levels will increase as we move to higher energy states.
To find the specific energy values, we need to solve the differential equation and apply the boundary conditions. The solutions will be in the form of a wavefunction ψ(x), and the corresponding energy levels E will be determined by the solutions.
Note: The specific solutions and energy levels will depend on the chosen unit system, such as the units used for the Planck constant (ħ) and the mass of the electron (m).

|
Explore Courses for Physics exam
|

|
Question Description
The energy of an electron moving in one dimension in an infinitely high potential box of width 1Å.Correct answer is '37.62'. Can you explain this answer? for Physics 2025 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about The energy of an electron moving in one dimension in an infinitely high potential box of width 1Å.Correct answer is '37.62'. Can you explain this answer? covers all topics & solutions for Physics 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The energy of an electron moving in one dimension in an infinitely high potential box of width 1Å.Correct answer is '37.62'. Can you explain this answer?.
The energy of an electron moving in one dimension in an infinitely high potential box of width 1Å.Correct answer is '37.62'. Can you explain this answer? for Physics 2025 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about The energy of an electron moving in one dimension in an infinitely high potential box of width 1Å.Correct answer is '37.62'. Can you explain this answer? covers all topics & solutions for Physics 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The energy of an electron moving in one dimension in an infinitely high potential box of width 1Å.Correct answer is '37.62'. Can you explain this answer?.
Solutions for The energy of an electron moving in one dimension in an infinitely high potential box of width 1Å.Correct answer is '37.62'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of The energy of an electron moving in one dimension in an infinitely high potential box of width 1Å.Correct answer is '37.62'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The energy of an electron moving in one dimension in an infinitely high potential box of width 1Å.Correct answer is '37.62'. Can you explain this answer?, a detailed solution for The energy of an electron moving in one dimension in an infinitely high potential box of width 1Å.Correct answer is '37.62'. Can you explain this answer? has been provided alongside types of The energy of an electron moving in one dimension in an infinitely high potential box of width 1Å.Correct answer is '37.62'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The energy of an electron moving in one dimension in an infinitely high potential box of width 1Å.Correct answer is '37.62'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















