CAT Exam > CAT Questions > A cube of 8 cm x 8 cm x 8 cm is divided into ...
Start Learning for Free
A cube of 8 cm x 8 cm x 8 cm is divided into smaller cubes of 1 cm x 1 cm x 1 cm and all the smaller cubes are numbered and arranged to form the larger cube. The smaller cubes are numbered such that the number on the cube represents the smallest volume enclosed by extending the sides of the cube to the outer surface of the largest cube and each cube bears the same number on each surface.
Q. Find the number of cubes bearing the numbers which are multiples of three.
- a)296
- b)256
- c)192
- d)512
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A cube of 8 cm x 8 cm x 8 cm is divided into smaller cubes of 1 cm x 1...
If we were to draw any surface of the cube it would be as follows:
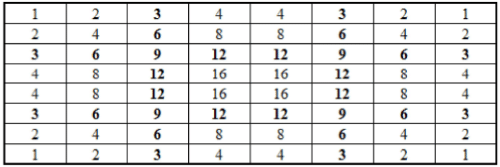
Consider the above surface as front surface.
The numbers in bold are multiples of three and the cubes behind it will also be its multiples.
So if we remove all the bold cubes and cubes (bearing numbers which are multiple of 3) behind them, the dimensions of the new cuboid will be 6 * 6 x 8.
The same process is followed for the remaining surfaces of the cube.
Dimensions of the resultant cuboid: 6 x 6 x 6 8 x 8 x 8 - 6 x 6 x 6 = 296
So, by now we have removed all the multiples of 3. i.e., we have removed 296 cubes. Thus, there are 296 cubes bearing the numbers which are multiples of three.
Hence, option 1.
Consider the above surface as front surface.
The numbers in bold are multiples of three and the cubes behind it will also be its multiples.
So if we remove all the bold cubes and cubes (bearing numbers which are multiple of 3) behind them, the dimensions of the new cuboid will be 6 * 6 x 8.
The same process is followed for the remaining surfaces of the cube.
Dimensions of the resultant cuboid: 6 x 6 x 6 8 x 8 x 8 - 6 x 6 x 6 = 296
So, by now we have removed all the multiples of 3. i.e., we have removed 296 cubes. Thus, there are 296 cubes bearing the numbers which are multiples of three.
Hence, option 1.
Most Upvoted Answer
A cube of 8 cm x 8 cm x 8 cm is divided into smaller cubes of 1 cm x 1...
To solve this problem, we need to understand the pattern in which the cubes are numbered and then count the number of cubes bearing numbers that are multiples of three.
Understanding the Numbering Pattern:
- The largest cube, with dimensions 8 cm x 8 cm x 8 cm, is divided into smaller cubes of 1 cm x 1 cm x 1 cm.
- The numbers on the cubes represent the smallest volume enclosed by extending the sides of the cube to the outer surface of the largest cube.
- Each cube bears the same number on each surface.
Counting the Cubes with Numbers that are Multiples of Three:
- Let's consider the cubes that are located on the corners of the larger cube.
- Each corner cube has three faces that are exposed, and the numbers on these faces are multiples of three.
- So, there are 8 corner cubes, each with 3 faces bearing numbers that are multiples of three, resulting in a total of 24 cubes with numbers that are multiples of three.
Now, let's consider the cubes that are located on the edges of the larger cube.
- Each edge cube has two faces that are exposed, and the numbers on these faces are multiples of three.
- There are 12 edge cubes on each edge of the larger cube, resulting in a total of 12 x 12 = 144 edge cubes.
- Each edge cube has 2 faces bearing numbers that are multiples of three, so the total number of cubes with numbers that are multiples of three on the edges is 144 x 2 = 288.
Finally, let's consider the cubes that are located on the faces of the larger cube that are not edges or corners.
- Each face cube has one face that is exposed, and the number on this face is a multiple of three.
- There are 6 faces on the larger cube, and each face has 6 x 6 = 36 face cubes.
- Each face cube has 1 face bearing a number that is a multiple of three, so the total number of face cubes with numbers that are multiples of three is 36 x 1 = 36.
Adding up the count from corner cubes, edge cubes, and face cubes, we get:
24 + 288 + 36 = 348.
However, we need to remember that each cube bears the same number on each surface. So, we have counted each cube three times (once for each face). Therefore, we need to divide the count by 3.
348 / 3 = 116.
Therefore, the correct answer is option A) 296, not option C) 192.
Therefore, the correct answer is option A) 296.
Understanding the Numbering Pattern:
- The largest cube, with dimensions 8 cm x 8 cm x 8 cm, is divided into smaller cubes of 1 cm x 1 cm x 1 cm.
- The numbers on the cubes represent the smallest volume enclosed by extending the sides of the cube to the outer surface of the largest cube.
- Each cube bears the same number on each surface.
Counting the Cubes with Numbers that are Multiples of Three:
- Let's consider the cubes that are located on the corners of the larger cube.
- Each corner cube has three faces that are exposed, and the numbers on these faces are multiples of three.
- So, there are 8 corner cubes, each with 3 faces bearing numbers that are multiples of three, resulting in a total of 24 cubes with numbers that are multiples of three.
Now, let's consider the cubes that are located on the edges of the larger cube.
- Each edge cube has two faces that are exposed, and the numbers on these faces are multiples of three.
- There are 12 edge cubes on each edge of the larger cube, resulting in a total of 12 x 12 = 144 edge cubes.
- Each edge cube has 2 faces bearing numbers that are multiples of three, so the total number of cubes with numbers that are multiples of three on the edges is 144 x 2 = 288.
Finally, let's consider the cubes that are located on the faces of the larger cube that are not edges or corners.
- Each face cube has one face that is exposed, and the number on this face is a multiple of three.
- There are 6 faces on the larger cube, and each face has 6 x 6 = 36 face cubes.
- Each face cube has 1 face bearing a number that is a multiple of three, so the total number of face cubes with numbers that are multiples of three is 36 x 1 = 36.
Adding up the count from corner cubes, edge cubes, and face cubes, we get:
24 + 288 + 36 = 348.
However, we need to remember that each cube bears the same number on each surface. So, we have counted each cube three times (once for each face). Therefore, we need to divide the count by 3.
348 / 3 = 116.
Therefore, the correct answer is option A) 296, not option C) 192.
Therefore, the correct answer is option A) 296.
Attention CAT Students!
To make sure you are not studying endlessly, EduRev has designed CAT study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in CAT.
|
Explore Courses for CAT exam
|
|
Similar CAT Doubts
Top Courses for CATView all
A cube of 8 cm x 8 cm x 8 cm is divided into smaller cubes of 1 cm x 1 cm x 1 cm and all the smaller cubes are numbered and arranged to form the larger cube. The smaller cubes are numbered such that the number on the cube represents the smallest volume enclosed by extending the sides of the cube to the outer surface of the largest cube and each cube bears the same number on each surface.Q.Find the number of cubes bearing the numbers which are multiples of three.a)296b)256c)192d)512Correct answer is option 'A'. Can you explain this answer?
Question Description
A cube of 8 cm x 8 cm x 8 cm is divided into smaller cubes of 1 cm x 1 cm x 1 cm and all the smaller cubes are numbered and arranged to form the larger cube. The smaller cubes are numbered such that the number on the cube represents the smallest volume enclosed by extending the sides of the cube to the outer surface of the largest cube and each cube bears the same number on each surface.Q.Find the number of cubes bearing the numbers which are multiples of three.a)296b)256c)192d)512Correct answer is option 'A'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about A cube of 8 cm x 8 cm x 8 cm is divided into smaller cubes of 1 cm x 1 cm x 1 cm and all the smaller cubes are numbered and arranged to form the larger cube. The smaller cubes are numbered such that the number on the cube represents the smallest volume enclosed by extending the sides of the cube to the outer surface of the largest cube and each cube bears the same number on each surface.Q.Find the number of cubes bearing the numbers which are multiples of three.a)296b)256c)192d)512Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A cube of 8 cm x 8 cm x 8 cm is divided into smaller cubes of 1 cm x 1 cm x 1 cm and all the smaller cubes are numbered and arranged to form the larger cube. The smaller cubes are numbered such that the number on the cube represents the smallest volume enclosed by extending the sides of the cube to the outer surface of the largest cube and each cube bears the same number on each surface.Q.Find the number of cubes bearing the numbers which are multiples of three.a)296b)256c)192d)512Correct answer is option 'A'. Can you explain this answer?.
A cube of 8 cm x 8 cm x 8 cm is divided into smaller cubes of 1 cm x 1 cm x 1 cm and all the smaller cubes are numbered and arranged to form the larger cube. The smaller cubes are numbered such that the number on the cube represents the smallest volume enclosed by extending the sides of the cube to the outer surface of the largest cube and each cube bears the same number on each surface.Q.Find the number of cubes bearing the numbers which are multiples of three.a)296b)256c)192d)512Correct answer is option 'A'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about A cube of 8 cm x 8 cm x 8 cm is divided into smaller cubes of 1 cm x 1 cm x 1 cm and all the smaller cubes are numbered and arranged to form the larger cube. The smaller cubes are numbered such that the number on the cube represents the smallest volume enclosed by extending the sides of the cube to the outer surface of the largest cube and each cube bears the same number on each surface.Q.Find the number of cubes bearing the numbers which are multiples of three.a)296b)256c)192d)512Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A cube of 8 cm x 8 cm x 8 cm is divided into smaller cubes of 1 cm x 1 cm x 1 cm and all the smaller cubes are numbered and arranged to form the larger cube. The smaller cubes are numbered such that the number on the cube represents the smallest volume enclosed by extending the sides of the cube to the outer surface of the largest cube and each cube bears the same number on each surface.Q.Find the number of cubes bearing the numbers which are multiples of three.a)296b)256c)192d)512Correct answer is option 'A'. Can you explain this answer?.
Solutions for A cube of 8 cm x 8 cm x 8 cm is divided into smaller cubes of 1 cm x 1 cm x 1 cm and all the smaller cubes are numbered and arranged to form the larger cube. The smaller cubes are numbered such that the number on the cube represents the smallest volume enclosed by extending the sides of the cube to the outer surface of the largest cube and each cube bears the same number on each surface.Q.Find the number of cubes bearing the numbers which are multiples of three.a)296b)256c)192d)512Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT.
Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
Here you can find the meaning of A cube of 8 cm x 8 cm x 8 cm is divided into smaller cubes of 1 cm x 1 cm x 1 cm and all the smaller cubes are numbered and arranged to form the larger cube. The smaller cubes are numbered such that the number on the cube represents the smallest volume enclosed by extending the sides of the cube to the outer surface of the largest cube and each cube bears the same number on each surface.Q.Find the number of cubes bearing the numbers which are multiples of three.a)296b)256c)192d)512Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A cube of 8 cm x 8 cm x 8 cm is divided into smaller cubes of 1 cm x 1 cm x 1 cm and all the smaller cubes are numbered and arranged to form the larger cube. The smaller cubes are numbered such that the number on the cube represents the smallest volume enclosed by extending the sides of the cube to the outer surface of the largest cube and each cube bears the same number on each surface.Q.Find the number of cubes bearing the numbers which are multiples of three.a)296b)256c)192d)512Correct answer is option 'A'. Can you explain this answer?, a detailed solution for A cube of 8 cm x 8 cm x 8 cm is divided into smaller cubes of 1 cm x 1 cm x 1 cm and all the smaller cubes are numbered and arranged to form the larger cube. The smaller cubes are numbered such that the number on the cube represents the smallest volume enclosed by extending the sides of the cube to the outer surface of the largest cube and each cube bears the same number on each surface.Q.Find the number of cubes bearing the numbers which are multiples of three.a)296b)256c)192d)512Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of A cube of 8 cm x 8 cm x 8 cm is divided into smaller cubes of 1 cm x 1 cm x 1 cm and all the smaller cubes are numbered and arranged to form the larger cube. The smaller cubes are numbered such that the number on the cube represents the smallest volume enclosed by extending the sides of the cube to the outer surface of the largest cube and each cube bears the same number on each surface.Q.Find the number of cubes bearing the numbers which are multiples of three.a)296b)256c)192d)512Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A cube of 8 cm x 8 cm x 8 cm is divided into smaller cubes of 1 cm x 1 cm x 1 cm and all the smaller cubes are numbered and arranged to form the larger cube. The smaller cubes are numbered such that the number on the cube represents the smallest volume enclosed by extending the sides of the cube to the outer surface of the largest cube and each cube bears the same number on each surface.Q.Find the number of cubes bearing the numbers which are multiples of three.a)296b)256c)192d)512Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice CAT tests.
|
|
Explore Courses for CAT exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup