All Courses
Explore Courses UPSC Exam UPSC Test Series Free Notes EduRev Infinity Get the App Login Join for Free
Sign in Open App
CAT Exam  >  CAT Questions  >  Group QuestionAnswer the following question b... Start Learning for Free
SaveJoin the Discussion on the App
Group Question
Answer the following question based on the information given below.
In the placement season of a leading management institute, all the available placements were offered to the prospective candidates in such a way that all the candidates got at least one job. The placements were from the following industries: Infrastructure, Services and Consultancy. None of the candidates got more than one job from the same industry.
There were 15 candidates who got placed in exactly one industry, while the number of candidates who got placed in all the three industries was not more than 5. The number of candidates who got placed in at least two industries, one of which is Services, was more than those who got placed in Infrastructure as well as Consultancy. The number of candidates who did not get placed in Services was the same as those who did not get placed in Consultancy, but was different from those who did not get placed in Infrastructure.
The number of candidates who got placed in Services as well as Consultancy was one more than those who got placed in Infrastructure as well as Services, but was one less than those who got placed in Infrastructure as well as Consultancy. The number of candidates who got placed only in Infrastructure was the same as those who got placed in Services as well as Consultancy, but not in Infrastructure.
It was further known that the number of prospective candidates that this institute had was less than 40. 
What was the maximum possible number of placements that were offered to the candidates in this institute?
  • a)
    48
  • b)
    70
  • c)
    84
  • d)
    66
Correct answer is option 'D'. Can you explain this answer?
Clear all your CAT doubts with EduRev
Verified Answer
Group QuestionAnswer the following question based on the information g...
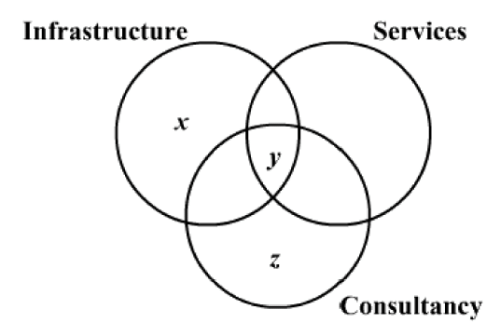
Let the number of candidates who got placed in only Infrastructure be x. Then, the number of candidates who got placed in Services as well as Consultancy, but not in Infrastructure is also x.
Let y be the number of candidates who got placed in all the three industries, then we have y < 5 ... (i) 
Let z be the number of candidates who got placed in only Consultancy. Then, we have the following graphical representation:
Now, the number of candidates who got placed in Services as well as Consultancy was one more than those who got placed in Infrastructure as well as Services, but was one less than those who got placed in Infrastructure as well as Consultancy. Since the number of candidates who got placed in Services as well as Consultancy (but not Infrastructure) is jc, hence the number of candidates who got placed in Infrastructure as well as Services (but not Consultancy) is (x - 1) and the number of candidates who got placed in Infrastructure and Consultancy (but not services) would be (x + 1).
Let p be the number of candidates who got placed in only Services. Since the number of candidates who did not get placed in Services is the same as those who did not get placed in Consultancy, we have: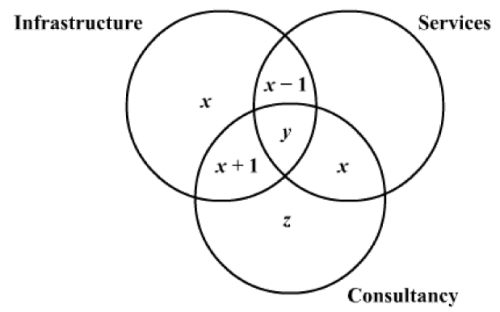
x + (x - 1) +p = x + (x + 1) + z; implying that p = z + 2 Hence, the final distribution would be as shown below:
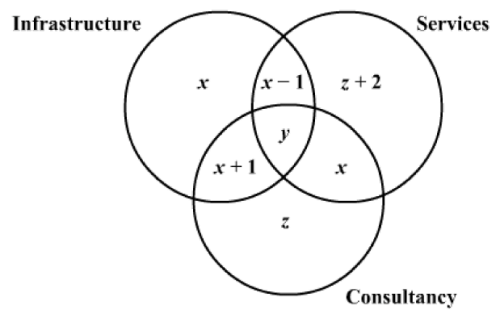
Now, since the total number of candidates in this institute was less than 40, we have;
4x + y + 2z + 2 < 40
Implying that 4x + y + 2z < 3 8                                 ... (ii)
Further, since the number of candidates who got placement from exactly one industry was 15, we have:
x + 2z + 2 = 15, implying x + 2z = 13                      ... (iii)
From (ii) and (iii), we get, 3x + y < 25                         ... (iv)
Now, since y cannot be negative, we have x < 8           ...(v)
The number of candidates who got placed in at least two industries, one of which is Services, is more than those who got placed in Infrastructure as well as Consultancy. Hence, we have,
2x+y—>x+y+9 implying x > 2
Thus, we have, 2 < x < 8 and further from (iii) x can take only odd values, hence x = 3 or 5 or 7
Case 1: If x = 3, then z = 5 Case 2: If x = 5, then z = 4 Case 3: Ifx = 7, thenz = 3
However, the number of candidates who did not get placed in Services was different from those who did not get placed in Infrastructure; i.e. 2x + z + 1 ^ x + 2z + 2 i.e. x^z + 1
Thus, Case 2 gets eliminated.
Hence, now we have two possibilities:
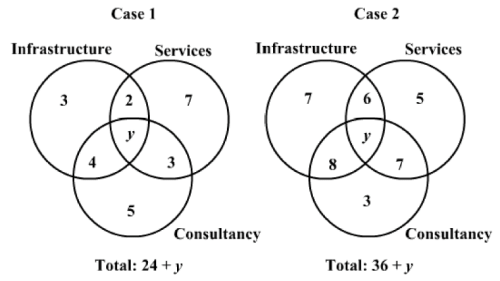
Since we are supposed to maximize the number of placements, this would be possible in Case 2, where the total number of candidates is 36 + y. Now since the maximum number of candidates in this institute is less than 40, we have 36 +y = 39, implying thaty = 3. Note that in Case 1, even though we get the total number of candidates as 24 +y = 39, implying thaty =15. However, since the maximum possible value ofy can be 5, the total number of placements can be (3 + 5 + 7) + 2(2 + 4 + 3) + 3(5) = 48.
Hence, from Case 2, the maximum number of placements would be: (7 + 5 + 3) + 2(6 + 8 + 7) + 3(3) = 15 + 42 + 9 = 66
Hence, option 4.
 
This question is part of UPSC exam. View all CAT courses
Most Upvoted Answer
Group QuestionAnswer the following question based on the information g...

Maximum Possible Number of Placements Offered

- Given Information:
- All candidates got at least one job.
- Industries: Infrastructure, Services, Consultancy.
- No candidate got more than one job from the same industry.
- 15 candidates placed in exactly one industry.
- Candidates placed in all three industries <=>
- Candidates placed in at least two industries, one being Services, > those in Infrastructure or Consultancy alone.
- Candidates not placed in Services = Candidates not placed in Consultancy ≠ Candidates not placed in Infrastructure.
- Candidates in Services & Consultancy = Candidates in Infrastructure & Services + 1 = Candidates in Infrastructure & Consultancy - 1.
- Candidates only in Infrastructure = Candidates in Services & Consultancy, but not in Infrastructure.

- Analysis:
- Let's assume the number of candidates in Services & Consultancy = x.
- Candidates in Infrastructure & Services = x - 1.
- Candidates in Infrastructure & Consultancy = x + 1.
- Total placements = 15 + x + (x - 1) + (x + 1) + x = 4x + 15.
- Maximum total placements occur when x is maximized.
- Considering x <= 5="" (candidates="" in="" all="" three="">
- Max total placements = 4(5) + 15 = 35 + 15 = 50.

Therefore, the maximum possible number of placements that were offered to the candidates in this institute is 50. Hence, option (d) 66 is incorrect.
Attention CAT Students!
To make sure you are not studying endlessly, EduRev has designed CAT study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in CAT.
Explore Courses for CAT exam

Similar CAT Doubts

In the placement season of a leading management institute, all the available placements were offered to the prospective candidates in such a way that all the candidates got at least one job. The placements were from the following industries: Infrastructure, Services and Consultancy. None of the candidates got more than one job from the same industry.There were 15 candidates who got placed in exactly one industry, while the number of candidates who got placed in all the three industries was not more than 5. The number of candidates who got placed in at least two industries, one of which is Services, was more than those who got placed in Infrastructure as well as Consultancy. The number of candidates who did not get placed in Services was the same as those who did not get placed in Consultancy, but was different from those who did not get placed in Infrastructure.The number of candidates who got placed in Services as well as Consultancy was one more than those who got placed in Infrastructure as well as Services, but was one less than those who got placed in Infrastructure as well as Consultancy. The number of candidates who got placed only in Infrastructure was the same as those who got placed in Services as well as Consultancy, but not in Infrastructure.It was further known that the number of prospective candidates that this institute had was less than 40.If there were a maximum of 35 candidates in the institute then which of the following statements is/are definitely true?

In the placement season of a leading management institute, all the available placements were offered to the prospective candidates in such a way that all the candidates got at least one job. The placements were from the following industries: Infrastructure, Services and Consultancy. None of the candidates got more than one job from the same industry.There were 15 candidates who got placed in exactly one industry, while the number of candidates who got placed in all the three industries was not more than 5. The number of candidates who got placed in at least two industries, one of which is Services, was more than those who got placed in Infrastructure as well as Consultancy. The number of candidates who did not get placed in Services was the same as those who did not get placed in Consultancy, but was different from those who did not get placed in Infrastructure.The number of candidates who got placed in Services as well as Consultancy was one more than those who got placed in Infrastructure as well as Services, but was one less than those who got placed in Infrastructure as well as Consultancy. The number of candidates who got placed only in Infrastructure was the same as those who got placed in Services as well as Consultancy, but not in Infrastructure.It was further known that the number of prospective candidates that this institute had was less than 40.Which of the following can be the number of candidates in this institute?

Directions: Answer the given question based on the following passage.For all the hype and the management charts and the impenetrable language, ultimately what the product consultancies sell is brains. Not the sort that have been schooled in a particular discipline, such as law or accountancy. But the kind that they hope could be set to resolving almost any business problem under the sun. No wonder, then that brains are at a premium; and no wonder that consultants are excited by what they call thought leadership.Ideas, they are convinced, are a source of competitive advantage. They help to attract customers. According to Richard Foster at McKinsey, consultancies now need to offer not just independent advice, but alternative ways of seeing the world. Bosses are endlessly curious about management theory, partly because they are always looking for ways of beating the competition, partly because more and more of them have studied management at business school.Ideas are useful for attracting and keeping clever recruits. Many MBA students go into consultancy because they think it will be more intellectually demanding and varied than mainstream management. Mr Gupta recalls that he joined McKinsey after Harvard because it seemed to be a sort of super business school. And many stay because they hope to produce a book or article that will turn them into gurus. Ideas are essential to corporate regeneration. Consultancies that merely apply peoples ideas rapidly go downhill.When it comes to producing those ground-breaking ideas, consultancies rely on a variety of techniques. First, they encourage their own people to be creative, using sabbaticals, promotions, prizes and pay rises as incentives. Gemini has established a thinking room in its Morristown headquarters where consultants can sit in isolation: booths, put on goggles and think deep thoughts. McKinsey is spending more money on intellectual capital, and is trying some structure on its traditionally laissez-faire approach to generating ideas. It is establishing research programmes on subjects such as growth, globalisation and the future shape of companies, and has set up a sort of internal mental Olympics in which 150 teams of junior McKinseyites compete to impress their seniors with their management thinking.The consultancies second line of approach is to form alliance with business schools and business thinkers. A.T. Kearney is sponsoring research on the future shape of companies at the Massachusetts Institute of Technology; Booz-Allen on the changing social contract at the London Business School; and Anderson Consulting on learning at Northwestern University, to name but three of hundreds of projects. CSC Index puts on seminars at which outside gurus ponder issues such as creativity or the changing role of chief executives.Yet the path to thought leadership is strewn with pitfalls. It is all very well to develop an eye-catching product such as re-engineering or Economic Value Added, and throw the weight of the organisation behind marketing it; but other companies, many of them with more resources, may pinch the lead and improve on it, and eventually the market for the product will cool, leaving its inventor desperate for something else to sell.Establishing and retaining intellectual leadership clearly takes strong management skills. Curiously enough in the management consultancy business these appear to be in short supply.Q.The author of the passage is LEAST likely to agree with which of the following statements?

Directions: Answer the given question based on the following passage.For all the hype and the management charts and the impenetrable language, ultimately what the product consultancies sell is brains. Not the sort that have been schooled in a particular discipline, such as law or accountancy. But the kind that they hope could be set to resolving almost any business problem under the sun. No wonder, then that brains are at a premium; and no wonder that consultants are excited by what they call thought leadership.Ideas, they are convinced, are a source of competitive advantage. They help to attract customers. According to Richard Foster at McKinsey, consultancies now need to offer not just independent advice, but alternative ways of seeing the world. Bosses are endlessly curious about management theory, partly because they are always looking for ways of beating the competition, partly because more and more of them have studied management at business school.Ideas are useful for attracting and keeping clever recruits. Many MBA students go into consultancy because they think it will be more intellectually demanding and varied than mainstream management. Mr Gupta recalls that he joined McKinsey after Harvard because it seemed to be a sort of super business school. And many stay because they hope to produce a book or article that will turn them into gurus. Ideas are essential to corporate regeneration. Consultancies that merely apply peoples ideas rapidly go downhill.When it comes to producing those ground-breaking ideas, consultancies rely on a variety of techniques. First, they encourage their own people to be creative, using sabbaticals, promotions, prizes and pay rises as incentives. Gemini has established a thinking room in its Morristown headquarters where consultants can sit in isolation: booths, put on goggles and think deep thoughts. McKinsey is spending more money on intellectual capital, and is trying some structure on its traditionally laissez-faire approach to generating ideas. It is establishing research programmes on subjects such as growth, globalisation and the future shape of companies, and has set up a sort of internal mental Olympics in which 150 teams of junior McKinseyites compete to impress their seniors with their management thinking.The consultancies second line of approach is to form alliance with business schools and business thinkers. A.T. Kearney is sponsoring research on the future shape of companies at the Massachusetts Institute of Technology; Booz-Allen on the changing social contract at the London Business School; and Anderson Consulting on learning at Northwestern University, to name but three of hundreds of projects. CSC Index puts on seminars at which outside gurus ponder issues such as creativity or the changing role of chief executives.Yet the path to thought leadership is strewn with pitfalls. It is all very well to develop an eye-catching product such as re-engineering or Economic Value Added, and throw the weight of the organisation behind marketing it; but other companies, many of them with more resources, may pinch the lead and improve on it, and eventually the market for the product will cool, leaving its inventor desperate for something else to sell.Establishing and retaining intellectual leadership clearly takes strong management skills. Curiously enough in the management consultancy business these appear to be in short supply.Q."Thought Leadership" is not an easy job. As indicated in the passage, which of the following can be the best reason for this?

Directions: Answer the given question based on the following passage.For all the hype and the management charts and the impenetrable language, ultimately what the product consultancies sell is brains. Not the sort that have been schooled in a particular discipline, such as law or accountancy. But the kind that they hope could be set to resolving almost any business problem under the sun. No wonder, then that brains are at a premium; and no wonder that consultants are excited by what they call thought leadership.Ideas, they are convinced, are a source of competitive advantage. They help to attract customers. According to Richard Foster at McKinsey, consultancies now need to offer not just independent advice, but alternative ways of seeing the world. Bosses are endlessly curious about management theory, partly because they are always looking for ways of beating the competition, partly because more and more of them have studied management at business school.Ideas are useful for attracting and keeping clever recruits. Many MBA students go into consultancy because they think it will be more intellectually demanding and varied than mainstream management. Mr Gupta recalls that he joined McKinsey after Harvard because it seemed to be a sort of super business school. And many stay because they hope to produce a book or article that will turn them into gurus. Ideas are essential to corporate regeneration. Consultancies that merely apply peoples ideas rapidly go downhill.When it comes to producing those ground-breaking ideas, consultancies rely on a variety of techniques. First, they encourage their own people to be creative, using sabbaticals, promotions, prizes and pay rises as incentives. Gemini has established a thinking room in its Morristown headquarters where consultants can sit in isolation: booths, put on goggles and think deep thoughts. McKinsey is spending more money on intellectual capital, and is trying some structure on its traditionally laissez-faire approach to generating ideas. It is establishing research programmes on subjects such as growth, globalisation and the future shape of companies, and has set up a sort of internal mental Olympics in which 150 teams of junior McKinseyites compete to impress their seniors with their management thinking.The consultancies second line of approach is to form alliance with business schools and business thinkers. A.T. Kearney is sponsoring research on the future shape of companies at the Massachusetts Institute of Technology; Booz-Allen on the changing social contract at the London Business School; and Anderson Consulting on learning at Northwestern University, to name but three of hundreds of projects. CSC Index puts on seminars at which outside gurus ponder issues such as creativity or the changing role of chief executives.Yet the path to thought leadership is strewn with pitfalls. It is all very well to develop an eye-catching product such as re-engineering or Economic Value Added, and throw the weight of the organisation behind marketing it; but other companies, many of them with more resources, may pinch the lead and improve on it, and eventually the market for the product will cool, leaving its inventor desperate for something else to sell.Establishing and retaining intellectual leadership clearly takes strong management skills. Curiously enough in the management consultancy business these appear to be in short supply.Q.According to the author, the threat to the concept of "thought leadership" is that

Top Courses for CATView all

Top Courses for CAT

Group QuestionAnswer the following question based on the information given below.In the placement season of a leading management institute, all the available placements were offered to the prospective candidates in such a way that all the candidates got at least one job. The placements were from the following industries: Infrastructure, Services and Consultancy. None of the candidates got more than one job from the same industry.There were 15 candidates who got placed in exactly one industry, while the number of candidates who got placed in all the three industries was not more than 5. The number of candidates who got placed in at least two industries, one of which is Services, was more than those who got placed in Infrastructure as well as Consultancy. The number of candidates who did not get placed in Services was the same as those who did not get placed in Consultancy, but was different from those who did not get placed in Infrastructure.The number of candidates who got placed in Services as well as Consultancy was one more than those who got placed in Infrastructure as well as Services, but was one less than those who got placed in Infrastructure as well as Consultancy. The number of candidates who got placed only in Infrastructure was the same as those who got placed in Services as well as Consultancy, but not in Infrastructure.It was further known that the number of prospective candidates that this institute had was less than 40.What was the maximum possible number of placements that were offeredto the candidates in this institute?a)48b)70c)84d)66Correct answer is option 'D'. Can you explain this answer?
Question Description
Group QuestionAnswer the following question based on the information given below.In the placement season of a leading management institute, all the available placements were offered to the prospective candidates in such a way that all the candidates got at least one job. The placements were from the following industries: Infrastructure, Services and Consultancy. None of the candidates got more than one job from the same industry.There were 15 candidates who got placed in exactly one industry, while the number of candidates who got placed in all the three industries was not more than 5. The number of candidates who got placed in at least two industries, one of which is Services, was more than those who got placed in Infrastructure as well as Consultancy. The number of candidates who did not get placed in Services was the same as those who did not get placed in Consultancy, but was different from those who did not get placed in Infrastructure.The number of candidates who got placed in Services as well as Consultancy was one more than those who got placed in Infrastructure as well as Services, but was one less than those who got placed in Infrastructure as well as Consultancy. The number of candidates who got placed only in Infrastructure was the same as those who got placed in Services as well as Consultancy, but not in Infrastructure.It was further known that the number of prospective candidates that this institute had was less than 40.What was the maximum possible number of placements that were offeredto the candidates in this institute?a)48b)70c)84d)66Correct answer is option 'D'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about Group QuestionAnswer the following question based on the information given below.In the placement season of a leading management institute, all the available placements were offered to the prospective candidates in such a way that all the candidates got at least one job. The placements were from the following industries: Infrastructure, Services and Consultancy. None of the candidates got more than one job from the same industry.There were 15 candidates who got placed in exactly one industry, while the number of candidates who got placed in all the three industries was not more than 5. The number of candidates who got placed in at least two industries, one of which is Services, was more than those who got placed in Infrastructure as well as Consultancy. The number of candidates who did not get placed in Services was the same as those who did not get placed in Consultancy, but was different from those who did not get placed in Infrastructure.The number of candidates who got placed in Services as well as Consultancy was one more than those who got placed in Infrastructure as well as Services, but was one less than those who got placed in Infrastructure as well as Consultancy. The number of candidates who got placed only in Infrastructure was the same as those who got placed in Services as well as Consultancy, but not in Infrastructure.It was further known that the number of prospective candidates that this institute had was less than 40.What was the maximum possible number of placements that were offeredto the candidates in this institute?a)48b)70c)84d)66Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Group QuestionAnswer the following question based on the information given below.In the placement season of a leading management institute, all the available placements were offered to the prospective candidates in such a way that all the candidates got at least one job. The placements were from the following industries: Infrastructure, Services and Consultancy. None of the candidates got more than one job from the same industry.There were 15 candidates who got placed in exactly one industry, while the number of candidates who got placed in all the three industries was not more than 5. The number of candidates who got placed in at least two industries, one of which is Services, was more than those who got placed in Infrastructure as well as Consultancy. The number of candidates who did not get placed in Services was the same as those who did not get placed in Consultancy, but was different from those who did not get placed in Infrastructure.The number of candidates who got placed in Services as well as Consultancy was one more than those who got placed in Infrastructure as well as Services, but was one less than those who got placed in Infrastructure as well as Consultancy. The number of candidates who got placed only in Infrastructure was the same as those who got placed in Services as well as Consultancy, but not in Infrastructure.It was further known that the number of prospective candidates that this institute had was less than 40.What was the maximum possible number of placements that were offeredto the candidates in this institute?a)48b)70c)84d)66Correct answer is option 'D'. Can you explain this answer?.
Solutions for Group QuestionAnswer the following question based on the information given below.In the placement season of a leading management institute, all the available placements were offered to the prospective candidates in such a way that all the candidates got at least one job. The placements were from the following industries: Infrastructure, Services and Consultancy. None of the candidates got more than one job from the same industry.There were 15 candidates who got placed in exactly one industry, while the number of candidates who got placed in all the three industries was not more than 5. The number of candidates who got placed in at least two industries, one of which is Services, was more than those who got placed in Infrastructure as well as Consultancy. The number of candidates who did not get placed in Services was the same as those who did not get placed in Consultancy, but was different from those who did not get placed in Infrastructure.The number of candidates who got placed in Services as well as Consultancy was one more than those who got placed in Infrastructure as well as Services, but was one less than those who got placed in Infrastructure as well as Consultancy. The number of candidates who got placed only in Infrastructure was the same as those who got placed in Services as well as Consultancy, but not in Infrastructure.It was further known that the number of prospective candidates that this institute had was less than 40.What was the maximum possible number of placements that were offeredto the candidates in this institute?a)48b)70c)84d)66Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT. Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
Here you can find the meaning of Group QuestionAnswer the following question based on the information given below.In the placement season of a leading management institute, all the available placements were offered to the prospective candidates in such a way that all the candidates got at least one job. The placements were from the following industries: Infrastructure, Services and Consultancy. None of the candidates got more than one job from the same industry.There were 15 candidates who got placed in exactly one industry, while the number of candidates who got placed in all the three industries was not more than 5. The number of candidates who got placed in at least two industries, one of which is Services, was more than those who got placed in Infrastructure as well as Consultancy. The number of candidates who did not get placed in Services was the same as those who did not get placed in Consultancy, but was different from those who did not get placed in Infrastructure.The number of candidates who got placed in Services as well as Consultancy was one more than those who got placed in Infrastructure as well as Services, but was one less than those who got placed in Infrastructure as well as Consultancy. The number of candidates who got placed only in Infrastructure was the same as those who got placed in Services as well as Consultancy, but not in Infrastructure.It was further known that the number of prospective candidates that this institute had was less than 40.What was the maximum possible number of placements that were offeredto the candidates in this institute?a)48b)70c)84d)66Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of Group QuestionAnswer the following question based on the information given below.In the placement season of a leading management institute, all the available placements were offered to the prospective candidates in such a way that all the candidates got at least one job. The placements were from the following industries: Infrastructure, Services and Consultancy. None of the candidates got more than one job from the same industry.There were 15 candidates who got placed in exactly one industry, while the number of candidates who got placed in all the three industries was not more than 5. The number of candidates who got placed in at least two industries, one of which is Services, was more than those who got placed in Infrastructure as well as Consultancy. The number of candidates who did not get placed in Services was the same as those who did not get placed in Consultancy, but was different from those who did not get placed in Infrastructure.The number of candidates who got placed in Services as well as Consultancy was one more than those who got placed in Infrastructure as well as Services, but was one less than those who got placed in Infrastructure as well as Consultancy. The number of candidates who got placed only in Infrastructure was the same as those who got placed in Services as well as Consultancy, but not in Infrastructure.It was further known that the number of prospective candidates that this institute had was less than 40.What was the maximum possible number of placements that were offeredto the candidates in this institute?a)48b)70c)84d)66Correct answer is option 'D'. Can you explain this answer?, a detailed solution for Group QuestionAnswer the following question based on the information given below.In the placement season of a leading management institute, all the available placements were offered to the prospective candidates in such a way that all the candidates got at least one job. The placements were from the following industries: Infrastructure, Services and Consultancy. None of the candidates got more than one job from the same industry.There were 15 candidates who got placed in exactly one industry, while the number of candidates who got placed in all the three industries was not more than 5. The number of candidates who got placed in at least two industries, one of which is Services, was more than those who got placed in Infrastructure as well as Consultancy. The number of candidates who did not get placed in Services was the same as those who did not get placed in Consultancy, but was different from those who did not get placed in Infrastructure.The number of candidates who got placed in Services as well as Consultancy was one more than those who got placed in Infrastructure as well as Services, but was one less than those who got placed in Infrastructure as well as Consultancy. The number of candidates who got placed only in Infrastructure was the same as those who got placed in Services as well as Consultancy, but not in Infrastructure.It was further known that the number of prospective candidates that this institute had was less than 40.What was the maximum possible number of placements that were offeredto the candidates in this institute?a)48b)70c)84d)66Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of Group QuestionAnswer the following question based on the information given below.In the placement season of a leading management institute, all the available placements were offered to the prospective candidates in such a way that all the candidates got at least one job. The placements were from the following industries: Infrastructure, Services and Consultancy. None of the candidates got more than one job from the same industry.There were 15 candidates who got placed in exactly one industry, while the number of candidates who got placed in all the three industries was not more than 5. The number of candidates who got placed in at least two industries, one of which is Services, was more than those who got placed in Infrastructure as well as Consultancy. The number of candidates who did not get placed in Services was the same as those who did not get placed in Consultancy, but was different from those who did not get placed in Infrastructure.The number of candidates who got placed in Services as well as Consultancy was one more than those who got placed in Infrastructure as well as Services, but was one less than those who got placed in Infrastructure as well as Consultancy. The number of candidates who got placed only in Infrastructure was the same as those who got placed in Services as well as Consultancy, but not in Infrastructure.It was further known that the number of prospective candidates that this institute had was less than 40.What was the maximum possible number of placements that were offeredto the candidates in this institute?a)48b)70c)84d)66Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an ample number of questions to practice Group QuestionAnswer the following question based on the information given below.In the placement season of a leading management institute, all the available placements were offered to the prospective candidates in such a way that all the candidates got at least one job. The placements were from the following industries: Infrastructure, Services and Consultancy. None of the candidates got more than one job from the same industry.There were 15 candidates who got placed in exactly one industry, while the number of candidates who got placed in all the three industries was not more than 5. The number of candidates who got placed in at least two industries, one of which is Services, was more than those who got placed in Infrastructure as well as Consultancy. The number of candidates who did not get placed in Services was the same as those who did not get placed in Consultancy, but was different from those who did not get placed in Infrastructure.The number of candidates who got placed in Services as well as Consultancy was one more than those who got placed in Infrastructure as well as Services, but was one less than those who got placed in Infrastructure as well as Consultancy. The number of candidates who got placed only in Infrastructure was the same as those who got placed in Services as well as Consultancy, but not in Infrastructure.It was further known that the number of prospective candidates that this institute had was less than 40.What was the maximum possible number of placements that were offeredto the candidates in this institute?a)48b)70c)84d)66Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice CAT tests.
Explore Courses for CAT exam

Top Courses for CAT

Explore Courses

Suggested Free Tests

Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
10M+ students study on EduRev
Get App
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup