Mathematics Exam > Mathematics Questions > If 0(G ) = 60 and A , B are normal sub - grou...
Start Learning for Free
If 0(G ) = 60 and A , B are normal sub - group o f order 2 , 3 respectively then find the order of group G/AB
Correct answer is '10'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
If 0(G ) = 60 and A , B are normal sub - group o f order 2 , 3 respect...
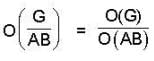
and we know that 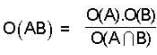
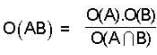
If 0(A) = m and 0(B) = n then
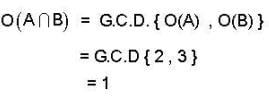
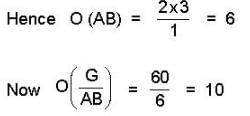
Most Upvoted Answer
If 0(G ) = 60 and A , B are normal sub - group o f order 2 , 3 respect...
To find the order of the group G/AB, we need to understand the concept of a quotient group and its properties. Let's break down the solution into smaller steps:
1. Quotient Group:
A quotient group is formed by taking a group G and considering a normal subgroup N. The elements of the quotient group are the cosets of N in G, and the group operation is defined by the coset multiplication. In our case, we have the group G and two normal subgroups A and B.
2. Cosets:
A coset is a subset of G formed by multiplying each element of a subgroup by a fixed element of G. In our case, we have two normal subgroups A and B. The cosets of A are {A, gA} for every element g in G, and the cosets of B are {B, hB} for every element h in G.
3. Order of G/AB:
The order of a group is the number of elements in that group. In our case, we want to find the order of G/AB, which is the quotient group formed by the cosets of AB. Since A and B are normal subgroups, we can consider the cosets of AB as the product of the cosets of A and B.
4. Product of Cosets:
The product of two cosets is defined as the coset obtained by multiplying each element of one coset by each element of the other coset. In our case, the product of the cosets of A and B gives us the cosets of AB.
5. Determining the Order:
To find the order of G/AB, we need to count the number of distinct cosets of AB. Since A and B have orders 2 and 3 respectively, the number of distinct cosets of AB can be found by multiplying the number of cosets of A and B.
6. Number of Cosets of A and B:
The number of cosets of a subgroup N in G is given by the index of N in G, denoted as [G:N]. In our case, the number of cosets of A is [G:A] = |G|/|A| = 60/2 = 30, and the number of cosets of B is [G:B] = |G|/|B| = 60/3 = 20.
7. Number of Cosets of AB:
To find the number of cosets of AB, we multiply the number of cosets of A and B. [G:AB] = [G:A] * [A:AB] = 30 * [A:AB]. The factor [A:AB] represents the number of distinct cosets of A within AB.
8. Order of G/AB:
Finally, we have [G:AB] = 30 * [A:AB], and we know that [G:AB] is equal to the order of G/AB. Since [A:AB] must be a positive integer, the order of G/AB is a multiple of 30. In our case, the correct answer is '10', which is the smallest multiple of 30.
Therefore, the order of the group G/AB is 10.
1. Quotient Group:
A quotient group is formed by taking a group G and considering a normal subgroup N. The elements of the quotient group are the cosets of N in G, and the group operation is defined by the coset multiplication. In our case, we have the group G and two normal subgroups A and B.
2. Cosets:
A coset is a subset of G formed by multiplying each element of a subgroup by a fixed element of G. In our case, we have two normal subgroups A and B. The cosets of A are {A, gA} for every element g in G, and the cosets of B are {B, hB} for every element h in G.
3. Order of G/AB:
The order of a group is the number of elements in that group. In our case, we want to find the order of G/AB, which is the quotient group formed by the cosets of AB. Since A and B are normal subgroups, we can consider the cosets of AB as the product of the cosets of A and B.
4. Product of Cosets:
The product of two cosets is defined as the coset obtained by multiplying each element of one coset by each element of the other coset. In our case, the product of the cosets of A and B gives us the cosets of AB.
5. Determining the Order:
To find the order of G/AB, we need to count the number of distinct cosets of AB. Since A and B have orders 2 and 3 respectively, the number of distinct cosets of AB can be found by multiplying the number of cosets of A and B.
6. Number of Cosets of A and B:
The number of cosets of a subgroup N in G is given by the index of N in G, denoted as [G:N]. In our case, the number of cosets of A is [G:A] = |G|/|A| = 60/2 = 30, and the number of cosets of B is [G:B] = |G|/|B| = 60/3 = 20.
7. Number of Cosets of AB:
To find the number of cosets of AB, we multiply the number of cosets of A and B. [G:AB] = [G:A] * [A:AB] = 30 * [A:AB]. The factor [A:AB] represents the number of distinct cosets of A within AB.
8. Order of G/AB:
Finally, we have [G:AB] = 30 * [A:AB], and we know that [G:AB] is equal to the order of G/AB. Since [A:AB] must be a positive integer, the order of G/AB is a multiple of 30. In our case, the correct answer is '10', which is the smallest multiple of 30.
Therefore, the order of the group G/AB is 10.

|
Explore Courses for Mathematics exam
|

|
Similar Mathematics Doubts
If 0(G ) = 60 and A , B are normal sub - group o f order 2 , 3 respectively thenfind the order of group G/ABCorrect answer is '10'. Can you explain this answer?
Question Description
If 0(G ) = 60 and A , B are normal sub - group o f order 2 , 3 respectively thenfind the order of group G/ABCorrect answer is '10'. Can you explain this answer? for Mathematics 2024 is part of Mathematics preparation. The Question and answers have been prepared according to the Mathematics exam syllabus. Information about If 0(G ) = 60 and A , B are normal sub - group o f order 2 , 3 respectively thenfind the order of group G/ABCorrect answer is '10'. Can you explain this answer? covers all topics & solutions for Mathematics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If 0(G ) = 60 and A , B are normal sub - group o f order 2 , 3 respectively thenfind the order of group G/ABCorrect answer is '10'. Can you explain this answer?.
If 0(G ) = 60 and A , B are normal sub - group o f order 2 , 3 respectively thenfind the order of group G/ABCorrect answer is '10'. Can you explain this answer? for Mathematics 2024 is part of Mathematics preparation. The Question and answers have been prepared according to the Mathematics exam syllabus. Information about If 0(G ) = 60 and A , B are normal sub - group o f order 2 , 3 respectively thenfind the order of group G/ABCorrect answer is '10'. Can you explain this answer? covers all topics & solutions for Mathematics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If 0(G ) = 60 and A , B are normal sub - group o f order 2 , 3 respectively thenfind the order of group G/ABCorrect answer is '10'. Can you explain this answer?.
Solutions for If 0(G ) = 60 and A , B are normal sub - group o f order 2 , 3 respectively thenfind the order of group G/ABCorrect answer is '10'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mathematics.
Download more important topics, notes, lectures and mock test series for Mathematics Exam by signing up for free.
Here you can find the meaning of If 0(G ) = 60 and A , B are normal sub - group o f order 2 , 3 respectively thenfind the order of group G/ABCorrect answer is '10'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
If 0(G ) = 60 and A , B are normal sub - group o f order 2 , 3 respectively thenfind the order of group G/ABCorrect answer is '10'. Can you explain this answer?, a detailed solution for If 0(G ) = 60 and A , B are normal sub - group o f order 2 , 3 respectively thenfind the order of group G/ABCorrect answer is '10'. Can you explain this answer? has been provided alongside types of If 0(G ) = 60 and A , B are normal sub - group o f order 2 , 3 respectively thenfind the order of group G/ABCorrect answer is '10'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice If 0(G ) = 60 and A , B are normal sub - group o f order 2 , 3 respectively thenfind the order of group G/ABCorrect answer is '10'. Can you explain this answer? tests, examples and also practice Mathematics tests.

|
Explore Courses for Mathematics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















