Class 10 Exam > Class 10 Questions > An equilateral triangle prism is arranged in ...
Start Learning for Free
An equilateral triangle prism is arranged in minimum deviation position for an angle of incidence of 45 degrees.the angle of minimum deviation is?
Most Upvoted Answer
An equilateral triangle prism is arranged in minimum deviation positio...
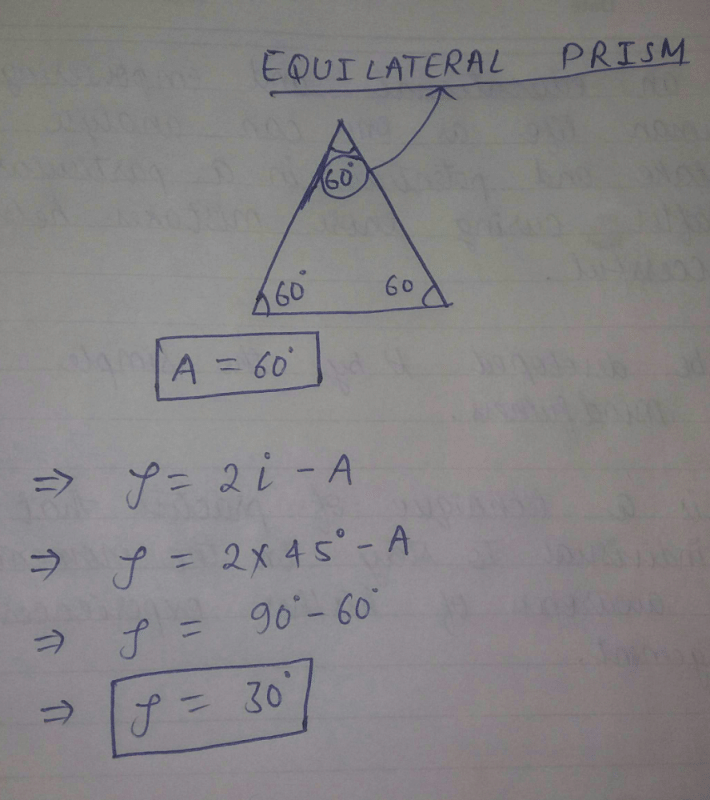
Community Answer
An equilateral triangle prism is arranged in minimum deviation positio...
Equilateral Triangle Prism and Minimum Deviation
Equilateral Triangle Prism
An equilateral triangle prism is a 3D shape with two parallel equilateral triangles as its bases and three rectangular faces connecting them. The three sides of the prism are also equal in length, making it a regular prism.
Minimum Deviation
The angle of minimum deviation is the angle at which light passing through a prism is deviated by the smallest possible angle. This angle is significant because it is the angle at which the light is refracted the least and therefore provides the most accurate measurements.
Arrangement for Minimum Deviation
Incident Angle of 45 Degrees
When light is incident on a prism, it refracts at the first surface, reflects off the second surface, and refracts again at the third surface. To achieve minimum deviation, the angle of incidence should be equal to the angle of emergence, and the prism should be arranged in such a way that the angle of deviation is minimized.
Arrangement of Prism
For an equilateral triangle prism, the angle of incidence that results in minimum deviation is 45 degrees. In this position, the prism is placed such that the incident light ray is perpendicular to one of the prism's faces and passes through the prism at an angle of 45 degrees to the base.
Determining the Angle of Minimum Deviation
Measuring Angle of Deviation
To determine the angle of minimum deviation, a ray of light is passed through the prism at the incident angle of 45 degrees. The angle of deviation is then measured by the difference between the angle of incidence and the angle of emergence.
Calculating the Angle of Minimum Deviation
The angle of minimum deviation can be calculated using the formula:
δm = (A + D)/2 - 60
where δm is the angle of minimum deviation, A is the angle of incidence, and D is the angle of deviation.
Conclusion
In conclusion, an equilateral triangle prism arranged in minimum deviation position for an angle of incidence of 45 degrees has an angle of minimum deviation that can be calculated using the formula δm = (A + D)/2 - 60. This angle is significant because it results in the most accurate measurements and is achieved by arranging the prism in a specific way.
Equilateral Triangle Prism
An equilateral triangle prism is a 3D shape with two parallel equilateral triangles as its bases and three rectangular faces connecting them. The three sides of the prism are also equal in length, making it a regular prism.
Minimum Deviation
The angle of minimum deviation is the angle at which light passing through a prism is deviated by the smallest possible angle. This angle is significant because it is the angle at which the light is refracted the least and therefore provides the most accurate measurements.
Arrangement for Minimum Deviation
Incident Angle of 45 Degrees
When light is incident on a prism, it refracts at the first surface, reflects off the second surface, and refracts again at the third surface. To achieve minimum deviation, the angle of incidence should be equal to the angle of emergence, and the prism should be arranged in such a way that the angle of deviation is minimized.
Arrangement of Prism
For an equilateral triangle prism, the angle of incidence that results in minimum deviation is 45 degrees. In this position, the prism is placed such that the incident light ray is perpendicular to one of the prism's faces and passes through the prism at an angle of 45 degrees to the base.
Determining the Angle of Minimum Deviation
Measuring Angle of Deviation
To determine the angle of minimum deviation, a ray of light is passed through the prism at the incident angle of 45 degrees. The angle of deviation is then measured by the difference between the angle of incidence and the angle of emergence.
Calculating the Angle of Minimum Deviation
The angle of minimum deviation can be calculated using the formula:
δm = (A + D)/2 - 60
where δm is the angle of minimum deviation, A is the angle of incidence, and D is the angle of deviation.
Conclusion
In conclusion, an equilateral triangle prism arranged in minimum deviation position for an angle of incidence of 45 degrees has an angle of minimum deviation that can be calculated using the formula δm = (A + D)/2 - 60. This angle is significant because it results in the most accurate measurements and is achieved by arranging the prism in a specific way.

|
Explore Courses for Class 10 exam
|

|
Similar Class 10 Doubts
Question Description
An equilateral triangle prism is arranged in minimum deviation position for an angle of incidence of 45 degrees.the angle of minimum deviation is? for Class 10 2025 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about An equilateral triangle prism is arranged in minimum deviation position for an angle of incidence of 45 degrees.the angle of minimum deviation is? covers all topics & solutions for Class 10 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An equilateral triangle prism is arranged in minimum deviation position for an angle of incidence of 45 degrees.the angle of minimum deviation is?.
An equilateral triangle prism is arranged in minimum deviation position for an angle of incidence of 45 degrees.the angle of minimum deviation is? for Class 10 2025 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about An equilateral triangle prism is arranged in minimum deviation position for an angle of incidence of 45 degrees.the angle of minimum deviation is? covers all topics & solutions for Class 10 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An equilateral triangle prism is arranged in minimum deviation position for an angle of incidence of 45 degrees.the angle of minimum deviation is?.
Solutions for An equilateral triangle prism is arranged in minimum deviation position for an angle of incidence of 45 degrees.the angle of minimum deviation is? in English & in Hindi are available as part of our courses for Class 10.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Here you can find the meaning of An equilateral triangle prism is arranged in minimum deviation position for an angle of incidence of 45 degrees.the angle of minimum deviation is? defined & explained in the simplest way possible. Besides giving the explanation of
An equilateral triangle prism is arranged in minimum deviation position for an angle of incidence of 45 degrees.the angle of minimum deviation is?, a detailed solution for An equilateral triangle prism is arranged in minimum deviation position for an angle of incidence of 45 degrees.the angle of minimum deviation is? has been provided alongside types of An equilateral triangle prism is arranged in minimum deviation position for an angle of incidence of 45 degrees.the angle of minimum deviation is? theory, EduRev gives you an
ample number of questions to practice An equilateral triangle prism is arranged in minimum deviation position for an angle of incidence of 45 degrees.the angle of minimum deviation is? tests, examples and also practice Class 10 tests.

|
Explore Courses for Class 10 exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























