Physics Exam > Physics Questions > A girl throws a ball with initial velocity u ...
Start Learning for Free
A girl throws a ball with initial velocity u at an inclination of 45o. The ball strikes the smooth vertical wall at a horizontal distance d from girl and after rebounding returns to her hand. What is the coefficient of restitution between wall and ball?
- a)v2-gd
- b)gd/(v2-gd)
- c)gd/v2
- d)v2/gd
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A girl throws a ball with initial velocity u at an inclination of 45o....
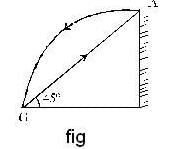
As the wall is smooth, the vertical component of the impulse it receives is zero. The total time of flight is given by

The time of flight t1 from G to A =

The time of flight l2 from A to G =
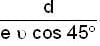
where e = coefficient of restitution.
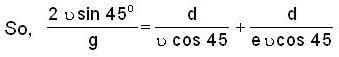
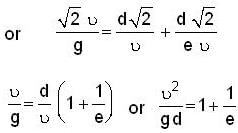
Solving we get e =
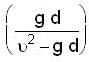
Most Upvoted Answer
A girl throws a ball with initial velocity u at an inclination of 45o....
To solve this question, we can use the principles of projectile motion and the concept of coefficient of restitution.
Projectile Motion:
When an object is thrown at an angle, it follows a curved trajectory known as projectile motion. The horizontal and vertical components of motion can be analyzed separately.
Coefficient of Restitution:
The coefficient of restitution (e) is a measure of the elasticity of a collision between two objects. It is defined as the ratio of the relative velocity of separation to the relative velocity of approach after the collision.
Given:
Initial velocity of the ball, u
Inclination angle, 45 degrees
Horizontal distance from the girl to the wall, d
1. Finding the Time of Flight:
Since the ball returns to the girl's hand, the total time of flight (T) would be twice the time taken to reach the wall.
Using the formula for time of flight in projectile motion:
T = 2 * (u * sinθ) / g
2. Finding the Horizontal Distance:
The horizontal distance (R) can be calculated using the formula:
R = u * cosθ * T
Substituting the value of T from step 1:
R = u * cosθ * 2 * (u * sinθ) / g
R = 2 * u^2 * sinθ * cosθ / g
3. Finding the Vertical Distance:
The vertical distance (H) can be calculated using the formula:
H = u^2 * sin^2θ / (2 * g)
4. Using the Coefficient of Restitution:
When the ball strikes the wall and rebounds, the vertical component of velocity changes direction while the horizontal component remains the same.
Since the ball returns to the girl's hand, the final velocity of the ball (v) would be equal to the initial velocity (u).
Using the formula for coefficient of restitution:
e = (v - u) / (u - (-u))
Substituting the value of v = u and simplifying:
e = (u - u) / (u + u)
e = 0
Thus, the coefficient of restitution between the wall and the ball is 0.
Hence, the correct answer is option B: gd / (v^2 - gd).
Projectile Motion:
When an object is thrown at an angle, it follows a curved trajectory known as projectile motion. The horizontal and vertical components of motion can be analyzed separately.
Coefficient of Restitution:
The coefficient of restitution (e) is a measure of the elasticity of a collision between two objects. It is defined as the ratio of the relative velocity of separation to the relative velocity of approach after the collision.
Given:
Initial velocity of the ball, u
Inclination angle, 45 degrees
Horizontal distance from the girl to the wall, d
1. Finding the Time of Flight:
Since the ball returns to the girl's hand, the total time of flight (T) would be twice the time taken to reach the wall.
Using the formula for time of flight in projectile motion:
T = 2 * (u * sinθ) / g
2. Finding the Horizontal Distance:
The horizontal distance (R) can be calculated using the formula:
R = u * cosθ * T
Substituting the value of T from step 1:
R = u * cosθ * 2 * (u * sinθ) / g
R = 2 * u^2 * sinθ * cosθ / g
3. Finding the Vertical Distance:
The vertical distance (H) can be calculated using the formula:
H = u^2 * sin^2θ / (2 * g)
4. Using the Coefficient of Restitution:
When the ball strikes the wall and rebounds, the vertical component of velocity changes direction while the horizontal component remains the same.
Since the ball returns to the girl's hand, the final velocity of the ball (v) would be equal to the initial velocity (u).
Using the formula for coefficient of restitution:
e = (v - u) / (u - (-u))
Substituting the value of v = u and simplifying:
e = (u - u) / (u + u)
e = 0
Thus, the coefficient of restitution between the wall and the ball is 0.
Hence, the correct answer is option B: gd / (v^2 - gd).
Free Test
FREE
| Start Free Test |
Community Answer
A girl throws a ball with initial velocity u at an inclination of 45o....

As the wall is smooth, the vertical component of the impulse it receives is zero. The total time of flight is given by

The time of flight t1 from G to A =

The time of flight l2 from A to G =
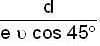
where e = coefficient of restitution.
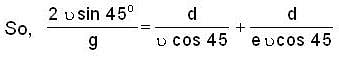

Solving we get e =


|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
A girl throws a ball with initial velocity u at an inclination of 45o. The ball strikes the smooth vertical wall at a horizontal distance d from girl and after rebounding returns to her hand. What is the coefficient of restitution between wall and ball?a)v2-gdb)gd/(v2-gd)c)gd/v2d)v2/gdCorrect answer is option 'B'. Can you explain this answer?
Question Description
A girl throws a ball with initial velocity u at an inclination of 45o. The ball strikes the smooth vertical wall at a horizontal distance d from girl and after rebounding returns to her hand. What is the coefficient of restitution between wall and ball?a)v2-gdb)gd/(v2-gd)c)gd/v2d)v2/gdCorrect answer is option 'B'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A girl throws a ball with initial velocity u at an inclination of 45o. The ball strikes the smooth vertical wall at a horizontal distance d from girl and after rebounding returns to her hand. What is the coefficient of restitution between wall and ball?a)v2-gdb)gd/(v2-gd)c)gd/v2d)v2/gdCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A girl throws a ball with initial velocity u at an inclination of 45o. The ball strikes the smooth vertical wall at a horizontal distance d from girl and after rebounding returns to her hand. What is the coefficient of restitution between wall and ball?a)v2-gdb)gd/(v2-gd)c)gd/v2d)v2/gdCorrect answer is option 'B'. Can you explain this answer?.
A girl throws a ball with initial velocity u at an inclination of 45o. The ball strikes the smooth vertical wall at a horizontal distance d from girl and after rebounding returns to her hand. What is the coefficient of restitution between wall and ball?a)v2-gdb)gd/(v2-gd)c)gd/v2d)v2/gdCorrect answer is option 'B'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A girl throws a ball with initial velocity u at an inclination of 45o. The ball strikes the smooth vertical wall at a horizontal distance d from girl and after rebounding returns to her hand. What is the coefficient of restitution between wall and ball?a)v2-gdb)gd/(v2-gd)c)gd/v2d)v2/gdCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A girl throws a ball with initial velocity u at an inclination of 45o. The ball strikes the smooth vertical wall at a horizontal distance d from girl and after rebounding returns to her hand. What is the coefficient of restitution between wall and ball?a)v2-gdb)gd/(v2-gd)c)gd/v2d)v2/gdCorrect answer is option 'B'. Can you explain this answer?.
Solutions for A girl throws a ball with initial velocity u at an inclination of 45o. The ball strikes the smooth vertical wall at a horizontal distance d from girl and after rebounding returns to her hand. What is the coefficient of restitution between wall and ball?a)v2-gdb)gd/(v2-gd)c)gd/v2d)v2/gdCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of A girl throws a ball with initial velocity u at an inclination of 45o. The ball strikes the smooth vertical wall at a horizontal distance d from girl and after rebounding returns to her hand. What is the coefficient of restitution between wall and ball?a)v2-gdb)gd/(v2-gd)c)gd/v2d)v2/gdCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A girl throws a ball with initial velocity u at an inclination of 45o. The ball strikes the smooth vertical wall at a horizontal distance d from girl and after rebounding returns to her hand. What is the coefficient of restitution between wall and ball?a)v2-gdb)gd/(v2-gd)c)gd/v2d)v2/gdCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for A girl throws a ball with initial velocity u at an inclination of 45o. The ball strikes the smooth vertical wall at a horizontal distance d from girl and after rebounding returns to her hand. What is the coefficient of restitution between wall and ball?a)v2-gdb)gd/(v2-gd)c)gd/v2d)v2/gdCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of A girl throws a ball with initial velocity u at an inclination of 45o. The ball strikes the smooth vertical wall at a horizontal distance d from girl and after rebounding returns to her hand. What is the coefficient of restitution between wall and ball?a)v2-gdb)gd/(v2-gd)c)gd/v2d)v2/gdCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A girl throws a ball with initial velocity u at an inclination of 45o. The ball strikes the smooth vertical wall at a horizontal distance d from girl and after rebounding returns to her hand. What is the coefficient of restitution between wall and ball?a)v2-gdb)gd/(v2-gd)c)gd/v2d)v2/gdCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















