Physics Exam > Physics Questions > A solid homogeneous cylinder of heighth= 1man...
Start Learning for Free
A solid homogeneous cylinder of height h = 1m and base r = 1m is kept vertically on a conveyor belt moving horizontally with an increasing velocity v = 1 + t2. If the cylinder is not allowed to slip find the time when the cylinder is about to topple.
Correct answer is '10'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A solid homogeneous cylinder of heighth= 1mand baser= 1m is kept verti...
WRT of belt, pseudo force ma act on cylinder at centre of mass as shown about to cylinder will be just about to topple when torque to weight w.r.t. P.
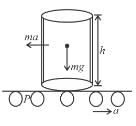
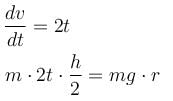
The correct answer is: 10
Most Upvoted Answer
A solid homogeneous cylinder of heighth= 1mand baser= 1m is kept verti...
WRT of belt, pseudo force ma act on cylinder at centre of mass as shown about to cylinder will be just about to topple when torque to weight w.r.t. P.
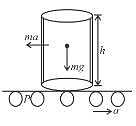
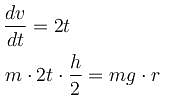
The correct answer is: 10
Free Test
FREE
| Start Free Test |
Community Answer
A solid homogeneous cylinder of heighth= 1mand baser= 1m is kept verti...
Problem:
A solid homogeneous cylinder of height h = 1 m and base radius r = 1 m is kept vertically on a conveyor belt moving horizontally with an increasing velocity v = t^2. If the cylinder is not allowed to slip, find the time when the cylinder is about to topple. The correct answer is '10'. Explain this answer in detail.
Solution:
To understand when the cylinder is about to topple, we need to consider the forces acting on it and analyze the conditions for equilibrium.
1. Forces Acting on the Cylinder:
When the cylinder is about to topple, the net torque acting on it must be zero. The forces acting on the cylinder are:
- Weight (mg) acting downward
- Normal force (N) exerted by the conveyor belt
- Frictional force (f) between the cylinder and the conveyor belt
2. Conditions for Equilibrium:
For the cylinder to be in equilibrium, the following conditions must be satisfied:
- Net force in the horizontal direction = 0
- Net torque about the point of contact with the conveyor belt = 0
3. Analysis:
Let's analyze the forces acting on the cylinder at a general time 't'.
- Weight (mg): The weight of the cylinder acts downward and can be calculated as mg = m * g, where m is the mass of the cylinder and g is the acceleration due to gravity.
- Normal force (N): The normal force exerted by the conveyor belt opposes the weight of the cylinder and acts upward. At equilibrium, N = mg.
- Frictional force (f): The frictional force between the cylinder and the conveyor belt acts in the opposite direction of the cylinder's motion. It can be calculated as f = μN, where μ is the coefficient of friction.
- Net force in the horizontal direction: The net force in the horizontal direction is given by F_net = f - m * a, where a is the acceleration of the cylinder.
- Net torque about the point of contact: The net torque about the point of contact with the conveyor belt is given by τ_net = r * f - r * m * a, where r is the radius of the cylinder.
4. Equilibrium Conditions:
Using the conditions for equilibrium, we can set up the following equations:
- Net force in the horizontal direction = 0:
f - m * a = 0
- Net torque about the point of contact = 0:
r * f - r * m * a = 0
5. Solving the Equations:
Substituting the expression for f from the first equation into the second equation, we get:
r * μN - r * m * a = 0
Substituting N = mg and rearranging the equation, we have:
r * μ * mg - r * m * a = 0
Simplifying the equation, we get:
μ * g - a = 0
Rearranging the equation, we have:
a = μ * g
6. Finding the Time When the Cylinder is about to Topple:
We are given that the velocity of the conveyor belt is v = t^2. Acceleration is the derivative of velocity with respect to time, so we differentiate the equation for velocity:
a
A solid homogeneous cylinder of height h = 1 m and base radius r = 1 m is kept vertically on a conveyor belt moving horizontally with an increasing velocity v = t^2. If the cylinder is not allowed to slip, find the time when the cylinder is about to topple. The correct answer is '10'. Explain this answer in detail.
Solution:
To understand when the cylinder is about to topple, we need to consider the forces acting on it and analyze the conditions for equilibrium.
1. Forces Acting on the Cylinder:
When the cylinder is about to topple, the net torque acting on it must be zero. The forces acting on the cylinder are:
- Weight (mg) acting downward
- Normal force (N) exerted by the conveyor belt
- Frictional force (f) between the cylinder and the conveyor belt
2. Conditions for Equilibrium:
For the cylinder to be in equilibrium, the following conditions must be satisfied:
- Net force in the horizontal direction = 0
- Net torque about the point of contact with the conveyor belt = 0
3. Analysis:
Let's analyze the forces acting on the cylinder at a general time 't'.
- Weight (mg): The weight of the cylinder acts downward and can be calculated as mg = m * g, where m is the mass of the cylinder and g is the acceleration due to gravity.
- Normal force (N): The normal force exerted by the conveyor belt opposes the weight of the cylinder and acts upward. At equilibrium, N = mg.
- Frictional force (f): The frictional force between the cylinder and the conveyor belt acts in the opposite direction of the cylinder's motion. It can be calculated as f = μN, where μ is the coefficient of friction.
- Net force in the horizontal direction: The net force in the horizontal direction is given by F_net = f - m * a, where a is the acceleration of the cylinder.
- Net torque about the point of contact: The net torque about the point of contact with the conveyor belt is given by τ_net = r * f - r * m * a, where r is the radius of the cylinder.
4. Equilibrium Conditions:
Using the conditions for equilibrium, we can set up the following equations:
- Net force in the horizontal direction = 0:
f - m * a = 0
- Net torque about the point of contact = 0:
r * f - r * m * a = 0
5. Solving the Equations:
Substituting the expression for f from the first equation into the second equation, we get:
r * μN - r * m * a = 0
Substituting N = mg and rearranging the equation, we have:
r * μ * mg - r * m * a = 0
Simplifying the equation, we get:
μ * g - a = 0
Rearranging the equation, we have:
a = μ * g
6. Finding the Time When the Cylinder is about to Topple:
We are given that the velocity of the conveyor belt is v = t^2. Acceleration is the derivative of velocity with respect to time, so we differentiate the equation for velocity:
a

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
A solid homogeneous cylinder of heighth= 1mand baser= 1m is kept vertically on a conveyor belt moving horizontally with an increasing velocityv= 1 +t2.If the cylinder is not allowed to slip find the time when the cylinder is about to topple.Correct answer is '10'. Can you explain this answer?
Question Description
A solid homogeneous cylinder of heighth= 1mand baser= 1m is kept vertically on a conveyor belt moving horizontally with an increasing velocityv= 1 +t2.If the cylinder is not allowed to slip find the time when the cylinder is about to topple.Correct answer is '10'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A solid homogeneous cylinder of heighth= 1mand baser= 1m is kept vertically on a conveyor belt moving horizontally with an increasing velocityv= 1 +t2.If the cylinder is not allowed to slip find the time when the cylinder is about to topple.Correct answer is '10'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A solid homogeneous cylinder of heighth= 1mand baser= 1m is kept vertically on a conveyor belt moving horizontally with an increasing velocityv= 1 +t2.If the cylinder is not allowed to slip find the time when the cylinder is about to topple.Correct answer is '10'. Can you explain this answer?.
A solid homogeneous cylinder of heighth= 1mand baser= 1m is kept vertically on a conveyor belt moving horizontally with an increasing velocityv= 1 +t2.If the cylinder is not allowed to slip find the time when the cylinder is about to topple.Correct answer is '10'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A solid homogeneous cylinder of heighth= 1mand baser= 1m is kept vertically on a conveyor belt moving horizontally with an increasing velocityv= 1 +t2.If the cylinder is not allowed to slip find the time when the cylinder is about to topple.Correct answer is '10'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A solid homogeneous cylinder of heighth= 1mand baser= 1m is kept vertically on a conveyor belt moving horizontally with an increasing velocityv= 1 +t2.If the cylinder is not allowed to slip find the time when the cylinder is about to topple.Correct answer is '10'. Can you explain this answer?.
Solutions for A solid homogeneous cylinder of heighth= 1mand baser= 1m is kept vertically on a conveyor belt moving horizontally with an increasing velocityv= 1 +t2.If the cylinder is not allowed to slip find the time when the cylinder is about to topple.Correct answer is '10'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of A solid homogeneous cylinder of heighth= 1mand baser= 1m is kept vertically on a conveyor belt moving horizontally with an increasing velocityv= 1 +t2.If the cylinder is not allowed to slip find the time when the cylinder is about to topple.Correct answer is '10'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A solid homogeneous cylinder of heighth= 1mand baser= 1m is kept vertically on a conveyor belt moving horizontally with an increasing velocityv= 1 +t2.If the cylinder is not allowed to slip find the time when the cylinder is about to topple.Correct answer is '10'. Can you explain this answer?, a detailed solution for A solid homogeneous cylinder of heighth= 1mand baser= 1m is kept vertically on a conveyor belt moving horizontally with an increasing velocityv= 1 +t2.If the cylinder is not allowed to slip find the time when the cylinder is about to topple.Correct answer is '10'. Can you explain this answer? has been provided alongside types of A solid homogeneous cylinder of heighth= 1mand baser= 1m is kept vertically on a conveyor belt moving horizontally with an increasing velocityv= 1 +t2.If the cylinder is not allowed to slip find the time when the cylinder is about to topple.Correct answer is '10'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A solid homogeneous cylinder of heighth= 1mand baser= 1m is kept vertically on a conveyor belt moving horizontally with an increasing velocityv= 1 +t2.If the cylinder is not allowed to slip find the time when the cylinder is about to topple.Correct answer is '10'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















