Physics Exam > Physics Questions > A uniform rod of length 75cmhinged at one end...
Start Learning for Free
A uniform rod of length 75 cm hinged at one ends and is free to rotate in vertical plane. It is released from rest when rods is horizontal. When the rod becomes vertical, it is broken at mid-point and lower part now moves freely. The distance of centre of lower part from it again becomes vertical for the first time is r. Find the approximate value of 2r.
Correct answer is '5'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A uniform rod of length 75cmhinged at one ends and is free to rotate i...
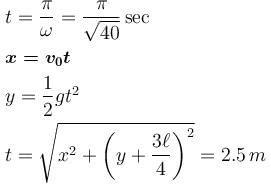

The correct answer is: 5
Most Upvoted Answer
A uniform rod of length 75cmhinged at one ends and is free to rotate i...
Given:
- Length of the uniform rod = 75 cm
- The rod is hinged at one end and can rotate freely in a vertical plane
- The rod is released from rest when it is horizontal
- When the rod becomes vertical, it is broken at the mid-point
- The lower part of the rod moves freely after it is broken
- The distance of the center of the lower part from the hinge again becomes vertical for the first time is 'r'
To find:
The approximate value of 2r
Approach:
1. The rod is initially horizontal and at rest. When it is released, it starts to fall due to the force of gravity acting on it.
2. As the rod falls, it gains angular momentum due to its length and mass distribution.
3. When the rod becomes vertical, it is broken at the mid-point. At this point, the angular momentum of the upper and lower parts of the rod is conserved.
4. The upper part of the rod continues to rotate freely, while the lower part starts to move in a circular path.
5. The center of the lower part of the rod moves in a circular arc with a radius 'r' and a center at the point where the rod was initially broken.
6. The distance of the center of the lower part from the hinge again becomes vertical for the first time when it reaches a height equal to the length of the upper part of the rod.
7. Since the length of the upper part of the rod is half of the total length, it becomes vertical when the center of the lower part is at a height of 37.5 cm.
8. Therefore, the value of 2r is equal to the distance between the hinge and the point where the center of the lower part becomes vertical again, which is 37.5 cm.
9. Hence, the approximate value of 2r is 5 times the value of r, i.e., 5.
Answer:
The approximate value of 2r is '5'.
- Length of the uniform rod = 75 cm
- The rod is hinged at one end and can rotate freely in a vertical plane
- The rod is released from rest when it is horizontal
- When the rod becomes vertical, it is broken at the mid-point
- The lower part of the rod moves freely after it is broken
- The distance of the center of the lower part from the hinge again becomes vertical for the first time is 'r'
To find:
The approximate value of 2r
Approach:
1. The rod is initially horizontal and at rest. When it is released, it starts to fall due to the force of gravity acting on it.
2. As the rod falls, it gains angular momentum due to its length and mass distribution.
3. When the rod becomes vertical, it is broken at the mid-point. At this point, the angular momentum of the upper and lower parts of the rod is conserved.
4. The upper part of the rod continues to rotate freely, while the lower part starts to move in a circular path.
5. The center of the lower part of the rod moves in a circular arc with a radius 'r' and a center at the point where the rod was initially broken.
6. The distance of the center of the lower part from the hinge again becomes vertical for the first time when it reaches a height equal to the length of the upper part of the rod.
7. Since the length of the upper part of the rod is half of the total length, it becomes vertical when the center of the lower part is at a height of 37.5 cm.
8. Therefore, the value of 2r is equal to the distance between the hinge and the point where the center of the lower part becomes vertical again, which is 37.5 cm.
9. Hence, the approximate value of 2r is 5 times the value of r, i.e., 5.
Answer:
The approximate value of 2r is '5'.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
A uniform rod of length 75cmhinged at one ends and is free to rotate in vertical plane. It is released from rest when rods is horizontal. When the rod becomes vertical, it is broken at mid-point and lower part now moves freely. The distance of centre of lower part from it again becomes vertical for the first time isr. Find the approximate value of 2r.Correct answer is '5'. Can you explain this answer?
Question Description
A uniform rod of length 75cmhinged at one ends and is free to rotate in vertical plane. It is released from rest when rods is horizontal. When the rod becomes vertical, it is broken at mid-point and lower part now moves freely. The distance of centre of lower part from it again becomes vertical for the first time isr. Find the approximate value of 2r.Correct answer is '5'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A uniform rod of length 75cmhinged at one ends and is free to rotate in vertical plane. It is released from rest when rods is horizontal. When the rod becomes vertical, it is broken at mid-point and lower part now moves freely. The distance of centre of lower part from it again becomes vertical for the first time isr. Find the approximate value of 2r.Correct answer is '5'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A uniform rod of length 75cmhinged at one ends and is free to rotate in vertical plane. It is released from rest when rods is horizontal. When the rod becomes vertical, it is broken at mid-point and lower part now moves freely. The distance of centre of lower part from it again becomes vertical for the first time isr. Find the approximate value of 2r.Correct answer is '5'. Can you explain this answer?.
A uniform rod of length 75cmhinged at one ends and is free to rotate in vertical plane. It is released from rest when rods is horizontal. When the rod becomes vertical, it is broken at mid-point and lower part now moves freely. The distance of centre of lower part from it again becomes vertical for the first time isr. Find the approximate value of 2r.Correct answer is '5'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A uniform rod of length 75cmhinged at one ends and is free to rotate in vertical plane. It is released from rest when rods is horizontal. When the rod becomes vertical, it is broken at mid-point and lower part now moves freely. The distance of centre of lower part from it again becomes vertical for the first time isr. Find the approximate value of 2r.Correct answer is '5'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A uniform rod of length 75cmhinged at one ends and is free to rotate in vertical plane. It is released from rest when rods is horizontal. When the rod becomes vertical, it is broken at mid-point and lower part now moves freely. The distance of centre of lower part from it again becomes vertical for the first time isr. Find the approximate value of 2r.Correct answer is '5'. Can you explain this answer?.
Solutions for A uniform rod of length 75cmhinged at one ends and is free to rotate in vertical plane. It is released from rest when rods is horizontal. When the rod becomes vertical, it is broken at mid-point and lower part now moves freely. The distance of centre of lower part from it again becomes vertical for the first time isr. Find the approximate value of 2r.Correct answer is '5'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of A uniform rod of length 75cmhinged at one ends and is free to rotate in vertical plane. It is released from rest when rods is horizontal. When the rod becomes vertical, it is broken at mid-point and lower part now moves freely. The distance of centre of lower part from it again becomes vertical for the first time isr. Find the approximate value of 2r.Correct answer is '5'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A uniform rod of length 75cmhinged at one ends and is free to rotate in vertical plane. It is released from rest when rods is horizontal. When the rod becomes vertical, it is broken at mid-point and lower part now moves freely. The distance of centre of lower part from it again becomes vertical for the first time isr. Find the approximate value of 2r.Correct answer is '5'. Can you explain this answer?, a detailed solution for A uniform rod of length 75cmhinged at one ends and is free to rotate in vertical plane. It is released from rest when rods is horizontal. When the rod becomes vertical, it is broken at mid-point and lower part now moves freely. The distance of centre of lower part from it again becomes vertical for the first time isr. Find the approximate value of 2r.Correct answer is '5'. Can you explain this answer? has been provided alongside types of A uniform rod of length 75cmhinged at one ends and is free to rotate in vertical plane. It is released from rest when rods is horizontal. When the rod becomes vertical, it is broken at mid-point and lower part now moves freely. The distance of centre of lower part from it again becomes vertical for the first time isr. Find the approximate value of 2r.Correct answer is '5'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A uniform rod of length 75cmhinged at one ends and is free to rotate in vertical plane. It is released from rest when rods is horizontal. When the rod becomes vertical, it is broken at mid-point and lower part now moves freely. The distance of centre of lower part from it again becomes vertical for the first time isr. Find the approximate value of 2r.Correct answer is '5'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















