**Explanation:**

To understand why the correct answer is option 'C', let's first define what it means for a discrete-time system to be unstable.

**Unstable System:**
In the context of control systems, an unstable system is one whose output grows without bound over time, even when subjected to bounded inputs. In other words, an unstable system is unable to reach a steady state and becomes increasingly unpredictable.

**Poles of the Z-Transfer Function:**
The poles of the z-transfer function represent the values of z for which the transfer function becomes infinite. These poles are determined by the denominator of the transfer function.

**Stability Analysis:**
The stability of a discrete-time system can be analyzed by examining the location of the poles of its transfer function in the z-plane. The z-plane is a complex plane where the real and imaginary parts of z are represented on the x and y axes, respectively.

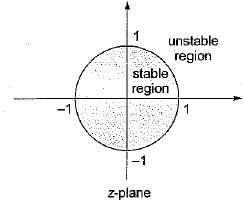
**Unit Circle:**
In the z-plane, the unit circle corresponds to all values of z with a magnitude of 1. This circle is important in stability analysis because it represents the boundary between stability and instability.

**Explanation of Options:**
a) On the left-half of z-plane: If all the poles of the z-transfer function are located on the left-half of the z-plane, it indicates stability. Therefore, this option is incorrect for an unstable system.

b) On the right-half of z-plane: If any pole of the z-transfer function lies on the right-half of the z-plane, it indicates instability. However, the question asks for all the poles to be in a specific region, so this option is also incorrect.

c) Outside the circle of unit radius: This option is correct because for a system to be unstable, at least one pole of the z-transfer function must lie outside the unit circle. When a pole is outside the unit circle, it indicates that the system's response will grow without bound and become unstable.

d) Within a circle of unit radius: If all the poles of the z-transfer function lie within the unit circle, it indicates stability. Therefore, this option is incorrect for an unstable system.

**Conclusion:**
In conclusion, for a discrete-time system to be unstable, at least one pole of the z-transfer function must lie outside the circle of unit radius in the z-plane. Therefore, the correct answer is option 'C'.