CA Foundation Exam > CA Foundation Questions > If all the observations are multiplied by 2, ...
Start Learning for Free
If all the observations are multiplied by 2, then
- a)New SD would be decreased by 2.
- b)New SD would be half of the previous SD
- c)New SD would be increased by 2
- d)New SD would be also multiplied by 2
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
If all the observations are multiplied by 2, thena)New SD would be dec...
If each observation is multiplied by 2, then mean(μ) will get doubled.
Now, variance
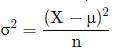
Now here both X and μ will be doubled, so the variance will become four times.
and SD is square root of variance, so SD will be double of initial SD
Most Upvoted Answer
If all the observations are multiplied by 2, thena)New SD would be dec...
Explanation:
Standard Deviation (SD) is a measure of the dispersion or variability of a set of data values. It is calculated as the square root of the variance.
When all the observations are multiplied by a constant, it affects the SD of the data. Let's see how:
- Effect of multiplying data by a constant: When all the observations in a data set are multiplied by a constant, it affects the measures of central tendency (mean, median, mode) and the measures of dispersion (range, interquartile range, variance, and SD) of the data. The effect on the measures of central tendency is straightforward - they are also multiplied by the same constant. The effect on the measures of dispersion is not as straightforward, and depends on the constant and the original SD of the data.
- New SD when all observations are multiplied by 2: When all the observations in a data set are multiplied by 2, the effect on the SD can be calculated as follows:
- The variance of the new data set is equal to the variance of the original data set multiplied by the square of the constant (2 in this case): Var(new) = Var(old) x 2^2 = 4Var(old)
- The SD of the new data set is equal to the square root of the variance of the new data set: SD(new) = √Var(new) = √(4Var(old)) = 2√Var(old)
- Therefore, the new SD is also multiplied by the constant (2 in this case).
- Example: Let's take an example to illustrate this. Suppose we have the following data set:
2, 4, 6, 8, 10
- The mean of this data set is 6.
- The SD of this data set is 2.83 (rounded to two decimal places).
- If we multiply all the observations by 2, we get:
4, 8, 12, 16, 20
- The mean of this new data set is 12.
- The SD of this new data set is 5.66 (rounded to two decimal places).
- The new SD is exactly twice the original SD, as predicted by our formula.
Therefore, the correct answer is option 'D': The new SD would be also multiplied by 2.
Standard Deviation (SD) is a measure of the dispersion or variability of a set of data values. It is calculated as the square root of the variance.
When all the observations are multiplied by a constant, it affects the SD of the data. Let's see how:
- Effect of multiplying data by a constant: When all the observations in a data set are multiplied by a constant, it affects the measures of central tendency (mean, median, mode) and the measures of dispersion (range, interquartile range, variance, and SD) of the data. The effect on the measures of central tendency is straightforward - they are also multiplied by the same constant. The effect on the measures of dispersion is not as straightforward, and depends on the constant and the original SD of the data.
- New SD when all observations are multiplied by 2: When all the observations in a data set are multiplied by 2, the effect on the SD can be calculated as follows:
- The variance of the new data set is equal to the variance of the original data set multiplied by the square of the constant (2 in this case): Var(new) = Var(old) x 2^2 = 4Var(old)
- The SD of the new data set is equal to the square root of the variance of the new data set: SD(new) = √Var(new) = √(4Var(old)) = 2√Var(old)
- Therefore, the new SD is also multiplied by the constant (2 in this case).
- Example: Let's take an example to illustrate this. Suppose we have the following data set:
2, 4, 6, 8, 10
- The mean of this data set is 6.
- The SD of this data set is 2.83 (rounded to two decimal places).
- If we multiply all the observations by 2, we get:
4, 8, 12, 16, 20
- The mean of this new data set is 12.
- The SD of this new data set is 5.66 (rounded to two decimal places).
- The new SD is exactly twice the original SD, as predicted by our formula.
Therefore, the correct answer is option 'D': The new SD would be also multiplied by 2.
Free Test
FREE
| Start Free Test |
Community Answer
If all the observations are multiplied by 2, thena)New SD would be dec...
D

|
Explore Courses for CA Foundation exam
|

|
Similar CA Foundation Doubts
If all the observations are multiplied by 2, thena)New SD would be decreased by 2.b)New SD would be half of the previous SDc)New SD would be increased by 2d)New SD would be also multiplied by 2Correct answer is option 'D'. Can you explain this answer?
Question Description
If all the observations are multiplied by 2, thena)New SD would be decreased by 2.b)New SD would be half of the previous SDc)New SD would be increased by 2d)New SD would be also multiplied by 2Correct answer is option 'D'. Can you explain this answer? for CA Foundation 2025 is part of CA Foundation preparation. The Question and answers have been prepared according to the CA Foundation exam syllabus. Information about If all the observations are multiplied by 2, thena)New SD would be decreased by 2.b)New SD would be half of the previous SDc)New SD would be increased by 2d)New SD would be also multiplied by 2Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for CA Foundation 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If all the observations are multiplied by 2, thena)New SD would be decreased by 2.b)New SD would be half of the previous SDc)New SD would be increased by 2d)New SD would be also multiplied by 2Correct answer is option 'D'. Can you explain this answer?.
If all the observations are multiplied by 2, thena)New SD would be decreased by 2.b)New SD would be half of the previous SDc)New SD would be increased by 2d)New SD would be also multiplied by 2Correct answer is option 'D'. Can you explain this answer? for CA Foundation 2025 is part of CA Foundation preparation. The Question and answers have been prepared according to the CA Foundation exam syllabus. Information about If all the observations are multiplied by 2, thena)New SD would be decreased by 2.b)New SD would be half of the previous SDc)New SD would be increased by 2d)New SD would be also multiplied by 2Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for CA Foundation 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If all the observations are multiplied by 2, thena)New SD would be decreased by 2.b)New SD would be half of the previous SDc)New SD would be increased by 2d)New SD would be also multiplied by 2Correct answer is option 'D'. Can you explain this answer?.
Solutions for If all the observations are multiplied by 2, thena)New SD would be decreased by 2.b)New SD would be half of the previous SDc)New SD would be increased by 2d)New SD would be also multiplied by 2Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for CA Foundation.
Download more important topics, notes, lectures and mock test series for CA Foundation Exam by signing up for free.
Here you can find the meaning of If all the observations are multiplied by 2, thena)New SD would be decreased by 2.b)New SD would be half of the previous SDc)New SD would be increased by 2d)New SD would be also multiplied by 2Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
If all the observations are multiplied by 2, thena)New SD would be decreased by 2.b)New SD would be half of the previous SDc)New SD would be increased by 2d)New SD would be also multiplied by 2Correct answer is option 'D'. Can you explain this answer?, a detailed solution for If all the observations are multiplied by 2, thena)New SD would be decreased by 2.b)New SD would be half of the previous SDc)New SD would be increased by 2d)New SD would be also multiplied by 2Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of If all the observations are multiplied by 2, thena)New SD would be decreased by 2.b)New SD would be half of the previous SDc)New SD would be increased by 2d)New SD would be also multiplied by 2Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice If all the observations are multiplied by 2, thena)New SD would be decreased by 2.b)New SD would be half of the previous SDc)New SD would be increased by 2d)New SD would be also multiplied by 2Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice CA Foundation tests.

|
Explore Courses for CA Foundation exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























