CAT Exam > CAT Questions > DIRECTIONS for questions: Answer the questio...
Start Learning for Free
DIRECTIONS for questions: Answer the questions on the basis of the information given below.
A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:
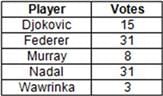
Further, it is also known that,
i. Murray was the only player who received the same number of votes in two or more rounds.
ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.
iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.
iv. in none of the rounds did more than one player receive the least number of votes.
Q. What is the total number of members in the panel who had to change the player that they voted for during any of the four rounds of voting?
- a)11
- b)12
- c)13
- d)14
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
DIRECTIONS for questions: Answer the questions on the basis of the in...
From the table we can see that Wawrinka must have been eliminated in the first round because he received only three votes. None of the other players could have received less than three votes, Hence, Wawrinka received three votes in the first round, In the second round, these 3 votes must be distributed across the remaining players. From (iii), Murray must have received at least 4 votes in the first round. Hence, he must have received 4 votes in the first and second rounds (from (i)). (Since he could not have received the same number of votes in at least two rounds - two votes each In rounds 2 and 3 is not possible because of (ii)). Since Murray is the only player to receive the same number of votes across at least two rounds, the remaining players must have had an increase in the number of votes that they received. Therefore, Djokovic, Federer and Nadal must each have received one additional vote in round 2. Djokovic must have received at least 4 votes in Round 1. Hence, he must have received at least 5 votes in Round 2. Also, Federer and Nadal could not have been eliminated in the 2nd round. Hence, Murray must have been eliminated in the second round. His 4 votes must be distributed across the remaining three players. Let a be the number of votes that Djokovic received in the first round, Hence, he must have received a+1 votes in the second round. In the third round, he must have received a + 2 or a + 3 votes (since the number of votes of Federer and Nadal must also have Increased by one each). Since Djokovic received a total of 15 voles, either 3a + 3 or 3a + 4, For a to be an integer, only 3a + 3 is possible and a = 4, Hence, Djokovic received 4, 5, 6 votes in 1st, 2nd and 3rd rounds respectively. Let b and c denote the number of votes that Federer and Nadal received during the first round. In the second round, they must have received b + 1 and c + 1. Since b + c = 11 (as there are 22 members i.e., 22 votes), b and c can only be 5 and 6 In any order, (b and c cannot be 4 since only two players received the same number of votes and b and c cannot be 3 from (iii)). In the second round, they must have received 6 and 7 votes. Since they could not have received the same number of votes in the final round (from (iv)), they must have received the same number of votes in round 3. Hence, they must have got 8 votes each in the third round. In the final round, they must have got 12 and 10 votes for them to have a total of 31 votes,
View all questions of this test
The following table gives the votes received by each player in each round.
Except for the members who voted for Federer and Nadal in the first round, the remaining members had to change the player that they voted for i.e., 11 members changed the player that they voted for.
Most Upvoted Answer
DIRECTIONS for questions: Answer the questions on the basis of the in...
From the table we can see that Wawrinka must have been eliminated in the first round because he received only three votes. None of the other players could have received less than three votes, Hence, Wawrinka received three votes in the first round, In the second round, these 3 votes must be distributed across the remaining players. From (iii), Murray must have received at least 4 votes in the first round. Hence, he must have received 4 votes in the first and second rounds (from (i)). (Since he could not have received the same number of votes in at least two rounds - two votes each In rounds 2 and 3 is not possible because of (ii)). Since Murray is the only player to receive the same number of votes across at least two rounds, the remaining players must have had an increase in the number of votes that they received. Therefore, Djokovic, Federer and Nadal must each have received one additional vote in round 2. Djokovic must have received at least 4 votes in Round 1. Hence, he must have received at least 5 votes in Round 2. Also, Federer and Nadal could not have been eliminated in the 2nd round. Hence, Murray must have been eliminated in the second round. His 4 votes must be distributed across the remaining three players. Let a be the number of votes that Djokovic received in the first round, Hence, he must have received a+1 votes in the second round. In the third round, he must have received a + 2 or a + 3 votes (since the number of votes of Federer and Nadal must also have Increased by one each). Since Djokovic received a total of 15 voles, either 3a + 3 or 3a + 4, For a to be an integer, only 3a + 3 is possible and a = 4, Hence, Djokovic received 4, 5, 6 votes in 1st, 2nd and 3rd rounds respectively. Let b and c denote the number of votes that Federer and Nadal received during the first round. In the second round, they must have received b + 1 and c + 1. Since b + c = 11 (as there are 22 members i.e., 22 votes), b and c can only be 5 and 6 In any order, (b and c cannot be 4 since only two players received the same number of votes and b and c cannot be 3 from (iii)). In the second round, they must have received 6 and 7 votes. Since they could not have received the same number of votes in the final round (from (iv)), they must have received the same number of votes in round 3. Hence, they must have got 8 votes each in the third round. In the final round, they must have got 12 and 10 votes for them to have a total of 31 votes,
The following table gives the votes received by each player in each round.
Except for the members who voted for Federer and Nadal in the first round, the remaining members had to change the player that they voted for i.e., 11 members changed the player that they voted for.
Attention CAT Students!
To make sure you are not studying endlessly, EduRev has designed CAT study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in CAT.
|
Explore Courses for CAT exam
|
|
Top Courses for CATView all
DIRECTIONS for questions: Answer the questions on the basis of the information given below.A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:Further, it is also known that, i. Murray was the only player who received the same number of votes in two or more rounds.ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.iv. in none of the rounds did more than one player receive the least number of votes.Q. What is the total number of members in the panel who had to change the player that they voted for during any of the four rounds of voting?a)11b)12c)13d)14Correct answer is option 'A'. Can you explain this answer?
Question Description
DIRECTIONS for questions: Answer the questions on the basis of the information given below.A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:Further, it is also known that, i. Murray was the only player who received the same number of votes in two or more rounds.ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.iv. in none of the rounds did more than one player receive the least number of votes.Q. What is the total number of members in the panel who had to change the player that they voted for during any of the four rounds of voting?a)11b)12c)13d)14Correct answer is option 'A'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about DIRECTIONS for questions: Answer the questions on the basis of the information given below.A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:Further, it is also known that, i. Murray was the only player who received the same number of votes in two or more rounds.ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.iv. in none of the rounds did more than one player receive the least number of votes.Q. What is the total number of members in the panel who had to change the player that they voted for during any of the four rounds of voting?a)11b)12c)13d)14Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for DIRECTIONS for questions: Answer the questions on the basis of the information given below.A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:Further, it is also known that, i. Murray was the only player who received the same number of votes in two or more rounds.ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.iv. in none of the rounds did more than one player receive the least number of votes.Q. What is the total number of members in the panel who had to change the player that they voted for during any of the four rounds of voting?a)11b)12c)13d)14Correct answer is option 'A'. Can you explain this answer?.
DIRECTIONS for questions: Answer the questions on the basis of the information given below.A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:Further, it is also known that, i. Murray was the only player who received the same number of votes in two or more rounds.ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.iv. in none of the rounds did more than one player receive the least number of votes.Q. What is the total number of members in the panel who had to change the player that they voted for during any of the four rounds of voting?a)11b)12c)13d)14Correct answer is option 'A'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about DIRECTIONS for questions: Answer the questions on the basis of the information given below.A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:Further, it is also known that, i. Murray was the only player who received the same number of votes in two or more rounds.ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.iv. in none of the rounds did more than one player receive the least number of votes.Q. What is the total number of members in the panel who had to change the player that they voted for during any of the four rounds of voting?a)11b)12c)13d)14Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for DIRECTIONS for questions: Answer the questions on the basis of the information given below.A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:Further, it is also known that, i. Murray was the only player who received the same number of votes in two or more rounds.ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.iv. in none of the rounds did more than one player receive the least number of votes.Q. What is the total number of members in the panel who had to change the player that they voted for during any of the four rounds of voting?a)11b)12c)13d)14Correct answer is option 'A'. Can you explain this answer?.
Solutions for DIRECTIONS for questions: Answer the questions on the basis of the information given below.A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:Further, it is also known that, i. Murray was the only player who received the same number of votes in two or more rounds.ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.iv. in none of the rounds did more than one player receive the least number of votes.Q. What is the total number of members in the panel who had to change the player that they voted for during any of the four rounds of voting?a)11b)12c)13d)14Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT.
Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
Here you can find the meaning of DIRECTIONS for questions: Answer the questions on the basis of the information given below.A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:Further, it is also known that, i. Murray was the only player who received the same number of votes in two or more rounds.ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.iv. in none of the rounds did more than one player receive the least number of votes.Q. What is the total number of members in the panel who had to change the player that they voted for during any of the four rounds of voting?a)11b)12c)13d)14Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
DIRECTIONS for questions: Answer the questions on the basis of the information given below.A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:Further, it is also known that, i. Murray was the only player who received the same number of votes in two or more rounds.ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.iv. in none of the rounds did more than one player receive the least number of votes.Q. What is the total number of members in the panel who had to change the player that they voted for during any of the four rounds of voting?a)11b)12c)13d)14Correct answer is option 'A'. Can you explain this answer?, a detailed solution for DIRECTIONS for questions: Answer the questions on the basis of the information given below.A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:Further, it is also known that, i. Murray was the only player who received the same number of votes in two or more rounds.ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.iv. in none of the rounds did more than one player receive the least number of votes.Q. What is the total number of members in the panel who had to change the player that they voted for during any of the four rounds of voting?a)11b)12c)13d)14Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of DIRECTIONS for questions: Answer the questions on the basis of the information given below.A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:Further, it is also known that, i. Murray was the only player who received the same number of votes in two or more rounds.ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.iv. in none of the rounds did more than one player receive the least number of votes.Q. What is the total number of members in the panel who had to change the player that they voted for during any of the four rounds of voting?a)11b)12c)13d)14Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice DIRECTIONS for questions: Answer the questions on the basis of the information given below.A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:Further, it is also known that, i. Murray was the only player who received the same number of votes in two or more rounds.ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.iv. in none of the rounds did more than one player receive the least number of votes.Q. What is the total number of members in the panel who had to change the player that they voted for during any of the four rounds of voting?a)11b)12c)13d)14Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice CAT tests.
|
|
Explore Courses for CAT exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup