Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > The channel width is to be contracted. The m...
Start Learning for Free
The channel width is to be contracted. The minimum width to which the channel can be contracted without affecting the upstream flow condition is
- a)4 m
- b)3.5 m
- c)3 m
- d)4.5 m
Correct answer is option 'A'. Can you explain this answer?
Most Upvoted Answer
The channel width is to be contracted. The minimum width to which the...
E1 = 1.9206 m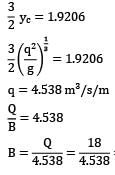
If upstream condition is not affected,
E1 = E2
Flow is sub-critical so we contract the width at section 2 depth of flow will decrease when the depth at section 2 is equal to critical depth flow at section 2 will be critical flow, beyond this further contraction will affect the upstream condition.
E2 = Ec = E1
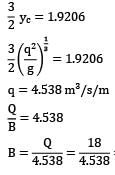
= 3.9665 m
Free Test
FREE
| Start Free Test |
Community Answer
The channel width is to be contracted. The minimum width to which the...
To understand why the minimum width to which the channel can be contracted without affecting the upstream flow condition is 4m, we need to consider the concept of critical flow in open channels.
Critical flow is the condition at which the specific energy of the flow is at its minimum for a given discharge. At critical flow, the flow velocity is maximum and the water surface slope is equal to the channel slope. If the channel width is reduced below a certain limit, it can disrupt the critical flow condition and cause the flow to become subcritical or supercritical.
Here's an explanation of why the correct answer is option 'A' (4m):
1. Critical Flow Condition:
In open channels, the critical flow condition is achieved when the Froude number (Fr) is equal to 1. The Froude number is defined as the ratio of the flow velocity to the velocity of small waves that can propagate on the water surface. Fr = V / sqrt(gd), where V is the flow velocity, g is the acceleration due to gravity, and d is the flow depth.
2. Width-Contraction Coefficient:
The width-contraction coefficient, also known as the contraction coefficient (Cc), is a dimensionless parameter that represents the reduction in channel width. Cc is defined as the ratio of the contracted width to the original width of the channel. Cc = Wc / Wo, where Wc is the contracted width and Wo is the original width of the channel.
3. Minimum Channel Width:
To maintain the critical flow condition, the minimum channel width can be determined using the following equation: Wo / Wc = 1 + (2/g)(Fr^2 - 1), where Wo is the original width and Wc is the contracted width.
4. Calculation:
Substituting the values, we have: Wo / Wc = 1 + (2/g)(1 - 1)
Simplifying further: Wo / Wc = 1
From the equation, we can see that the contracted width (Wc) should be equal to the original width (Wo) to maintain the critical flow condition. Therefore, the minimum width to which the channel can be contracted without affecting the upstream flow condition is 4m (option 'A').
Critical flow is the condition at which the specific energy of the flow is at its minimum for a given discharge. At critical flow, the flow velocity is maximum and the water surface slope is equal to the channel slope. If the channel width is reduced below a certain limit, it can disrupt the critical flow condition and cause the flow to become subcritical or supercritical.
Here's an explanation of why the correct answer is option 'A' (4m):
1. Critical Flow Condition:
In open channels, the critical flow condition is achieved when the Froude number (Fr) is equal to 1. The Froude number is defined as the ratio of the flow velocity to the velocity of small waves that can propagate on the water surface. Fr = V / sqrt(gd), where V is the flow velocity, g is the acceleration due to gravity, and d is the flow depth.
2. Width-Contraction Coefficient:
The width-contraction coefficient, also known as the contraction coefficient (Cc), is a dimensionless parameter that represents the reduction in channel width. Cc is defined as the ratio of the contracted width to the original width of the channel. Cc = Wc / Wo, where Wc is the contracted width and Wo is the original width of the channel.
3. Minimum Channel Width:
To maintain the critical flow condition, the minimum channel width can be determined using the following equation: Wo / Wc = 1 + (2/g)(Fr^2 - 1), where Wo is the original width and Wc is the contracted width.
4. Calculation:
Substituting the values, we have: Wo / Wc = 1 + (2/g)(1 - 1)
Simplifying further: Wo / Wc = 1
From the equation, we can see that the contracted width (Wc) should be equal to the original width (Wo) to maintain the critical flow condition. Therefore, the minimum width to which the channel can be contracted without affecting the upstream flow condition is 4m (option 'A').

|
Explore Courses for Civil Engineering (CE) exam
|

|
Similar Civil Engineering (CE) Doubts
The channel width is to be contracted. The minimum width to which the channel can be contracted without affecting the upstream flow condition isa) 4 mb) 3.5 mc) 3 md) 4.5 mCorrect answer is option 'A'. Can you explain this answer?
Question Description
The channel width is to be contracted. The minimum width to which the channel can be contracted without affecting the upstream flow condition isa) 4 mb) 3.5 mc) 3 md) 4.5 mCorrect answer is option 'A'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about The channel width is to be contracted. The minimum width to which the channel can be contracted without affecting the upstream flow condition isa) 4 mb) 3.5 mc) 3 md) 4.5 mCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The channel width is to be contracted. The minimum width to which the channel can be contracted without affecting the upstream flow condition isa) 4 mb) 3.5 mc) 3 md) 4.5 mCorrect answer is option 'A'. Can you explain this answer?.
The channel width is to be contracted. The minimum width to which the channel can be contracted without affecting the upstream flow condition isa) 4 mb) 3.5 mc) 3 md) 4.5 mCorrect answer is option 'A'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about The channel width is to be contracted. The minimum width to which the channel can be contracted without affecting the upstream flow condition isa) 4 mb) 3.5 mc) 3 md) 4.5 mCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The channel width is to be contracted. The minimum width to which the channel can be contracted without affecting the upstream flow condition isa) 4 mb) 3.5 mc) 3 md) 4.5 mCorrect answer is option 'A'. Can you explain this answer?.
Solutions for The channel width is to be contracted. The minimum width to which the channel can be contracted without affecting the upstream flow condition isa) 4 mb) 3.5 mc) 3 md) 4.5 mCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of The channel width is to be contracted. The minimum width to which the channel can be contracted without affecting the upstream flow condition isa) 4 mb) 3.5 mc) 3 md) 4.5 mCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The channel width is to be contracted. The minimum width to which the channel can be contracted without affecting the upstream flow condition isa) 4 mb) 3.5 mc) 3 md) 4.5 mCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for The channel width is to be contracted. The minimum width to which the channel can be contracted without affecting the upstream flow condition isa) 4 mb) 3.5 mc) 3 md) 4.5 mCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of The channel width is to be contracted. The minimum width to which the channel can be contracted without affecting the upstream flow condition isa) 4 mb) 3.5 mc) 3 md) 4.5 mCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The channel width is to be contracted. The minimum width to which the channel can be contracted without affecting the upstream flow condition isa) 4 mb) 3.5 mc) 3 md) 4.5 mCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























