Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > A rectangular open channel of width 6.5 m is...
Start Learning for Free
A rectangular open channel of width 6.5 m is carrying a discharge of 150 m3/s. The critical depth of the channel is __________. (in meters, upto two decimal places) [take g = 9.81 m/s2]
Correct answer is 'Range: 3.76 to 3.80'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A rectangular open channel of width 6.5 m is carrying a discharge of ...
Width of channel [B] = 6.5 m Discharge [Q] = 150m3/s For rectangular channel critical depth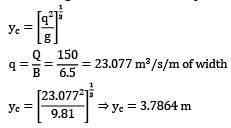
View all questions of this test
Most Upvoted Answer
A rectangular open channel of width 6.5 m is carrying a discharge of ...
The critical depth of an open channel
In fluid mechanics, the critical depth of an open channel is the depth at which the flow velocity is at its maximum for a given discharge. It is a significant parameter in the design and analysis of open channel flow.
Governing equation for critical depth
The critical depth can be determined using the Manning's equation:
V = (1/n) * R^(2/3) * S^(1/2)
Where:
- V is the flow velocity
- n is the Manning's roughness coefficient
- R is the hydraulic radius
- S is the slope of the energy grade line
Calculating the critical depth
To calculate the critical depth, we need to rearrange the Manning's equation in terms of depth.
V = (1/n) * R^(2/3) * S^(1/2)
V = (1/n) * (A/P)^(2/3) * S^(1/2)
V = (1/n) * (A^(2/3) * P^(-2/3)) * S^(1/2)
V = (1/n) * (A^(2/3) * (2A/H)^(2/3)) * S^(1/2)
V = (1/n) * (2A^(5/3) * H^(-2/3)) * S^(1/2)
V = (2/n) * (A^(5/3) * H^(-2/3)) * S^(1/2)
V = (2/n) * (Q/A) * H^(5/3) * A^(-2/3) * S^(1/2)
V = (2/n) * (Q/A) * H^(5/3) * (Q/A)^(-2/3) * S^(1/2)
V = (2/n) * (Q/A) * Q^(-2/3) * S^(1/2)
V = (2/n) * Q^(1/3) * A^(-2/3) * S^(1/2)
V = (2/n) * Q^(1/3) * (B * H) ^(-2/3) * S^(1/2)
Attention Civil Engineering (CE) Students!
To make sure you are not studying endlessly, EduRev has designed Civil Engineering (CE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Civil Engineering (CE).
|
Explore Courses for Civil Engineering (CE) exam
|
|
Similar Civil Engineering (CE) Doubts
Top Courses for Civil Engineering (CE)View all
A rectangular open channel of width 6.5 m is carrying a discharge of 150 m3/s. The critical depth of the channel is __________. (in meters, upto two decimal places) [take g = 9.81 m/s2]Correct answer is 'Range: 3.76 to 3.80'. Can you explain this answer?
Question Description
A rectangular open channel of width 6.5 m is carrying a discharge of 150 m3/s. The critical depth of the channel is __________. (in meters, upto two decimal places) [take g = 9.81 m/s2]Correct answer is 'Range: 3.76 to 3.80'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A rectangular open channel of width 6.5 m is carrying a discharge of 150 m3/s. The critical depth of the channel is __________. (in meters, upto two decimal places) [take g = 9.81 m/s2]Correct answer is 'Range: 3.76 to 3.80'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A rectangular open channel of width 6.5 m is carrying a discharge of 150 m3/s. The critical depth of the channel is __________. (in meters, upto two decimal places) [take g = 9.81 m/s2]Correct answer is 'Range: 3.76 to 3.80'. Can you explain this answer?.
A rectangular open channel of width 6.5 m is carrying a discharge of 150 m3/s. The critical depth of the channel is __________. (in meters, upto two decimal places) [take g = 9.81 m/s2]Correct answer is 'Range: 3.76 to 3.80'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A rectangular open channel of width 6.5 m is carrying a discharge of 150 m3/s. The critical depth of the channel is __________. (in meters, upto two decimal places) [take g = 9.81 m/s2]Correct answer is 'Range: 3.76 to 3.80'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A rectangular open channel of width 6.5 m is carrying a discharge of 150 m3/s. The critical depth of the channel is __________. (in meters, upto two decimal places) [take g = 9.81 m/s2]Correct answer is 'Range: 3.76 to 3.80'. Can you explain this answer?.
Solutions for A rectangular open channel of width 6.5 m is carrying a discharge of 150 m3/s. The critical depth of the channel is __________. (in meters, upto two decimal places) [take g = 9.81 m/s2]Correct answer is 'Range: 3.76 to 3.80'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of A rectangular open channel of width 6.5 m is carrying a discharge of 150 m3/s. The critical depth of the channel is __________. (in meters, upto two decimal places) [take g = 9.81 m/s2]Correct answer is 'Range: 3.76 to 3.80'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A rectangular open channel of width 6.5 m is carrying a discharge of 150 m3/s. The critical depth of the channel is __________. (in meters, upto two decimal places) [take g = 9.81 m/s2]Correct answer is 'Range: 3.76 to 3.80'. Can you explain this answer?, a detailed solution for A rectangular open channel of width 6.5 m is carrying a discharge of 150 m3/s. The critical depth of the channel is __________. (in meters, upto two decimal places) [take g = 9.81 m/s2]Correct answer is 'Range: 3.76 to 3.80'. Can you explain this answer? has been provided alongside types of A rectangular open channel of width 6.5 m is carrying a discharge of 150 m3/s. The critical depth of the channel is __________. (in meters, upto two decimal places) [take g = 9.81 m/s2]Correct answer is 'Range: 3.76 to 3.80'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A rectangular open channel of width 6.5 m is carrying a discharge of 150 m3/s. The critical depth of the channel is __________. (in meters, upto two decimal places) [take g = 9.81 m/s2]Correct answer is 'Range: 3.76 to 3.80'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.
|
|
Explore Courses for Civil Engineering (CE) exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup