Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > A radial flow hydraulic turbine is required ...
Start Learning for Free
A radial flow hydraulic turbine is required to be designed to produce 20 MW under a head of 16 m at a speed of 90 rpm. A geometrically similar model with an output of 30 kW and a head of 4 m is to be tested under dynamically similar conditions. What is the required impeller diameter ratio between the model and prototype?
Correct answer is 'Range: 0.1 to 0.2'. Can you explain this answer?
Most Upvoted Answer
A radial flow hydraulic turbine is required to be designed to produce...
Equating the power coefficients (π term containing the power P) for the model and prototype, we can write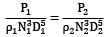
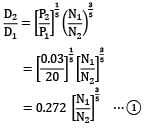
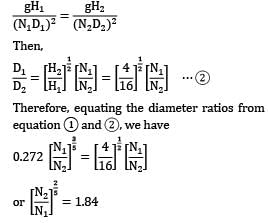
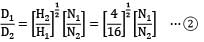
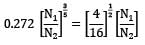
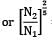
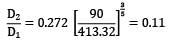
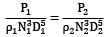
(where subscript 1 refers to the prototype and subscript 2 to the model) Considering the fluids to be incompressible, and same for both the prototype and model, we have
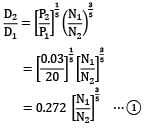
Equating the head coefficients (π term containing the head H)
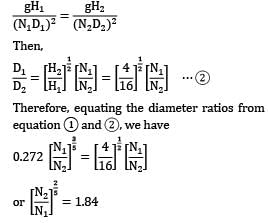
Then,
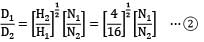
Therefore equating the diameter ratios from equation 1 and 2 we have
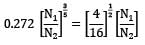
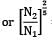
= 1.84
Hence, N2 = N1(1.84)5/2 = 90 × (1.84)5/2
= 413.32 rpm
From equation ①
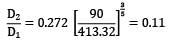
Free Test
FREE
| Start Free Test |
Community Answer
A radial flow hydraulic turbine is required to be designed to produce...
Problem Statement:
A radial flow hydraulic turbine is required to be designed to produce 20 MW under a head of 16 m at a speed of 90 rpm. A geometrically similar model with an output of 30 kW and a head of 4 m is to be tested under dynamically similar conditions. What is the required impeller diameter ratio between the model and prototype?
Solution:
To find the required impeller diameter ratio between the model and prototype, we need to apply the concept of dynamic similarity. Dynamic similarity refers to the similarity in the flow conditions and forces acting on the model and prototype.
Step 1: Calculate the specific speed of the prototype turbine:
The specific speed (Ns) of a hydraulic turbine is given by the formula:
Ns = (N * √P) / (H)^(3/4)
Where,
N = Speed of the turbine (rpm)
P = Power output of the turbine (kW)
H = Head of water (m)
Given:
N = 90 rpm
P = 20,000 kW
H = 16 m
Substituting the values in the formula, we can find the specific speed of the prototype turbine:
Ns = (90 * √20,000) / (16)^(3/4)
Ns = 257.94
Step 2: Calculate the specific speed of the model turbine:
The specific speed of the model turbine can be calculated using the concept of dynamic similarity. Since the model and prototype turbines are dynamically similar, their specific speeds should be the same.
Given:
P (model) = 30 kW
H (model) = 4 m
Substituting the values in the formula, we can find the specific speed of the model turbine:
Ns (model) = (N (model) * √P (model)) / (H (model))^(3/4)
Ns (model) = (90 * √30) / (4)^(3/4)
Ns (model) = 241.66
Step 3: Calculate the required impeller diameter ratio:
The impeller diameter ratio (D) between the model and prototype turbines can be calculated using the specific speed ratio (Ns ratio) and the head ratio (H ratio). The formula for calculating the impeller diameter ratio is:
D = (Ns (model) / Ns) * (H / H (model))^(1/4)
Given:
Ns (model) = 241.66
Ns = 257.94
H = 16 m
H (model) = 4 m
Substituting the values in the formula, we can find the required impeller diameter ratio:
D = (241.66 / 257.94) * (16 / 4)^(1/4)
D = 0.1805
Therefore, the required impeller diameter ratio between the model and prototype turbines is approximately 0.1805, which falls within the given range of 0.1 to 0.2.
A radial flow hydraulic turbine is required to be designed to produce 20 MW under a head of 16 m at a speed of 90 rpm. A geometrically similar model with an output of 30 kW and a head of 4 m is to be tested under dynamically similar conditions. What is the required impeller diameter ratio between the model and prototype?
Solution:
To find the required impeller diameter ratio between the model and prototype, we need to apply the concept of dynamic similarity. Dynamic similarity refers to the similarity in the flow conditions and forces acting on the model and prototype.
Step 1: Calculate the specific speed of the prototype turbine:
The specific speed (Ns) of a hydraulic turbine is given by the formula:
Ns = (N * √P) / (H)^(3/4)
Where,
N = Speed of the turbine (rpm)
P = Power output of the turbine (kW)
H = Head of water (m)
Given:
N = 90 rpm
P = 20,000 kW
H = 16 m
Substituting the values in the formula, we can find the specific speed of the prototype turbine:
Ns = (90 * √20,000) / (16)^(3/4)
Ns = 257.94
Step 2: Calculate the specific speed of the model turbine:
The specific speed of the model turbine can be calculated using the concept of dynamic similarity. Since the model and prototype turbines are dynamically similar, their specific speeds should be the same.
Given:
P (model) = 30 kW
H (model) = 4 m
Substituting the values in the formula, we can find the specific speed of the model turbine:
Ns (model) = (N (model) * √P (model)) / (H (model))^(3/4)
Ns (model) = (90 * √30) / (4)^(3/4)
Ns (model) = 241.66
Step 3: Calculate the required impeller diameter ratio:
The impeller diameter ratio (D) between the model and prototype turbines can be calculated using the specific speed ratio (Ns ratio) and the head ratio (H ratio). The formula for calculating the impeller diameter ratio is:
D = (Ns (model) / Ns) * (H / H (model))^(1/4)
Given:
Ns (model) = 241.66
Ns = 257.94
H = 16 m
H (model) = 4 m
Substituting the values in the formula, we can find the required impeller diameter ratio:
D = (241.66 / 257.94) * (16 / 4)^(1/4)
D = 0.1805
Therefore, the required impeller diameter ratio between the model and prototype turbines is approximately 0.1805, which falls within the given range of 0.1 to 0.2.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Similar Civil Engineering (CE) Doubts
A radial flow hydraulic turbine is required to be designed to produce 20 MW under a head of 16 m at a speed of 90 rpm. A geometrically similar model with an output of 30 kW and a head of 4 m is to be tested under dynamically similar conditions. What is the required impeller diameter ratio between the model and prototype?Correct answer is 'Range: 0.1 to 0.2'. Can you explain this answer?
Question Description
A radial flow hydraulic turbine is required to be designed to produce 20 MW under a head of 16 m at a speed of 90 rpm. A geometrically similar model with an output of 30 kW and a head of 4 m is to be tested under dynamically similar conditions. What is the required impeller diameter ratio between the model and prototype?Correct answer is 'Range: 0.1 to 0.2'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A radial flow hydraulic turbine is required to be designed to produce 20 MW under a head of 16 m at a speed of 90 rpm. A geometrically similar model with an output of 30 kW and a head of 4 m is to be tested under dynamically similar conditions. What is the required impeller diameter ratio between the model and prototype?Correct answer is 'Range: 0.1 to 0.2'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A radial flow hydraulic turbine is required to be designed to produce 20 MW under a head of 16 m at a speed of 90 rpm. A geometrically similar model with an output of 30 kW and a head of 4 m is to be tested under dynamically similar conditions. What is the required impeller diameter ratio between the model and prototype?Correct answer is 'Range: 0.1 to 0.2'. Can you explain this answer?.
A radial flow hydraulic turbine is required to be designed to produce 20 MW under a head of 16 m at a speed of 90 rpm. A geometrically similar model with an output of 30 kW and a head of 4 m is to be tested under dynamically similar conditions. What is the required impeller diameter ratio between the model and prototype?Correct answer is 'Range: 0.1 to 0.2'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A radial flow hydraulic turbine is required to be designed to produce 20 MW under a head of 16 m at a speed of 90 rpm. A geometrically similar model with an output of 30 kW and a head of 4 m is to be tested under dynamically similar conditions. What is the required impeller diameter ratio between the model and prototype?Correct answer is 'Range: 0.1 to 0.2'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A radial flow hydraulic turbine is required to be designed to produce 20 MW under a head of 16 m at a speed of 90 rpm. A geometrically similar model with an output of 30 kW and a head of 4 m is to be tested under dynamically similar conditions. What is the required impeller diameter ratio between the model and prototype?Correct answer is 'Range: 0.1 to 0.2'. Can you explain this answer?.
Solutions for A radial flow hydraulic turbine is required to be designed to produce 20 MW under a head of 16 m at a speed of 90 rpm. A geometrically similar model with an output of 30 kW and a head of 4 m is to be tested under dynamically similar conditions. What is the required impeller diameter ratio between the model and prototype?Correct answer is 'Range: 0.1 to 0.2'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of A radial flow hydraulic turbine is required to be designed to produce 20 MW under a head of 16 m at a speed of 90 rpm. A geometrically similar model with an output of 30 kW and a head of 4 m is to be tested under dynamically similar conditions. What is the required impeller diameter ratio between the model and prototype?Correct answer is 'Range: 0.1 to 0.2'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A radial flow hydraulic turbine is required to be designed to produce 20 MW under a head of 16 m at a speed of 90 rpm. A geometrically similar model with an output of 30 kW and a head of 4 m is to be tested under dynamically similar conditions. What is the required impeller diameter ratio between the model and prototype?Correct answer is 'Range: 0.1 to 0.2'. Can you explain this answer?, a detailed solution for A radial flow hydraulic turbine is required to be designed to produce 20 MW under a head of 16 m at a speed of 90 rpm. A geometrically similar model with an output of 30 kW and a head of 4 m is to be tested under dynamically similar conditions. What is the required impeller diameter ratio between the model and prototype?Correct answer is 'Range: 0.1 to 0.2'. Can you explain this answer? has been provided alongside types of A radial flow hydraulic turbine is required to be designed to produce 20 MW under a head of 16 m at a speed of 90 rpm. A geometrically similar model with an output of 30 kW and a head of 4 m is to be tested under dynamically similar conditions. What is the required impeller diameter ratio between the model and prototype?Correct answer is 'Range: 0.1 to 0.2'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A radial flow hydraulic turbine is required to be designed to produce 20 MW under a head of 16 m at a speed of 90 rpm. A geometrically similar model with an output of 30 kW and a head of 4 m is to be tested under dynamically similar conditions. What is the required impeller diameter ratio between the model and prototype?Correct answer is 'Range: 0.1 to 0.2'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























