SSC Exam > SSC Questions > What is the number of instantaneous centres ...
Start Learning for Free
What is the number of instantaneous centres of rotation for a 6-link mechanism?
- a)4
- b)6
- c)12
- d)15
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
What is the number of instantaneous centres of rotation for a 6-link ...
The number of instantaneous centres in a constrained kinematic chain is equal to the number of possible combinations of two links.
The number of instantaneous centres:
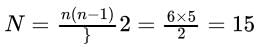
where n is the number of links.
Most Upvoted Answer
What is the number of instantaneous centres of rotation for a 6-link ...
The number of instantaneous centres in a constrained kinematic chain is equal to the number of possible combinations of two links.
The number of instantaneous centres:
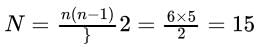
where n is the number of links.
Free Test
FREE
| Start Free Test |
Community Answer
What is the number of instantaneous centres of rotation for a 6-link ...
Understanding Instantaneous Centres of Rotation
Instantaneous centres of rotation (ICR) are crucial in analyzing the motion of mechanisms. For a planar mechanism composed of links, the ICR helps determine the velocity of various points on the links.
Formula for Instantaneous Centres
The number of instantaneous centres in a mechanism can be calculated using the formula:
- N = (n - 1)(n - 2) / 2
Where N is the number of instantaneous centres, and n is the number of links in the mechanism.
Application to a 6-Link Mechanism
For a 6-link mechanism (n = 6):
- N = (6 - 1)(6 - 2) / 2
- N = (5)(4) / 2
- N = 20 / 2
- N = 10
However, this formula accounts for the number of distinct pairs of links. To find the total number of instantaneous centres, we consider the additional constraints and interactions between the links, which can lead to overlaps and additional ICRs in certain configurations.
Final Count of Instantaneous Centres
In practice, when analyzing a 6-link mechanism, the total number of unique instantaneous centres can be derived based on the specific arrangement and connectivity of the links. Thus, after considering these factors:
- The correct number of instantaneous centres for a 6-link mechanism is 15.
Conclusion
Therefore, the correct answer is option 'D' (15). Understanding the mechanics of these centres aids in the efficient design and analysis of complex mechanical systems.
Instantaneous centres of rotation (ICR) are crucial in analyzing the motion of mechanisms. For a planar mechanism composed of links, the ICR helps determine the velocity of various points on the links.
Formula for Instantaneous Centres
The number of instantaneous centres in a mechanism can be calculated using the formula:
- N = (n - 1)(n - 2) / 2
Where N is the number of instantaneous centres, and n is the number of links in the mechanism.
Application to a 6-Link Mechanism
For a 6-link mechanism (n = 6):
- N = (6 - 1)(6 - 2) / 2
- N = (5)(4) / 2
- N = 20 / 2
- N = 10
However, this formula accounts for the number of distinct pairs of links. To find the total number of instantaneous centres, we consider the additional constraints and interactions between the links, which can lead to overlaps and additional ICRs in certain configurations.
Final Count of Instantaneous Centres
In practice, when analyzing a 6-link mechanism, the total number of unique instantaneous centres can be derived based on the specific arrangement and connectivity of the links. Thus, after considering these factors:
- The correct number of instantaneous centres for a 6-link mechanism is 15.
Conclusion
Therefore, the correct answer is option 'D' (15). Understanding the mechanics of these centres aids in the efficient design and analysis of complex mechanical systems.
|
Explore Courses for SSC exam
|
|
Similar SSC Doubts
What is the number of instantaneous centres of rotation for a 6-link mechanism?a)4b)6c)12d)15Correct answer is option 'D'. Can you explain this answer?
Question Description
What is the number of instantaneous centres of rotation for a 6-link mechanism?a)4b)6c)12d)15Correct answer is option 'D'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about What is the number of instantaneous centres of rotation for a 6-link mechanism?a)4b)6c)12d)15Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for What is the number of instantaneous centres of rotation for a 6-link mechanism?a)4b)6c)12d)15Correct answer is option 'D'. Can you explain this answer?.
What is the number of instantaneous centres of rotation for a 6-link mechanism?a)4b)6c)12d)15Correct answer is option 'D'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about What is the number of instantaneous centres of rotation for a 6-link mechanism?a)4b)6c)12d)15Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for What is the number of instantaneous centres of rotation for a 6-link mechanism?a)4b)6c)12d)15Correct answer is option 'D'. Can you explain this answer?.
Solutions for What is the number of instantaneous centres of rotation for a 6-link mechanism?a)4b)6c)12d)15Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for SSC.
Download more important topics, notes, lectures and mock test series for SSC Exam by signing up for free.
Here you can find the meaning of What is the number of instantaneous centres of rotation for a 6-link mechanism?a)4b)6c)12d)15Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
What is the number of instantaneous centres of rotation for a 6-link mechanism?a)4b)6c)12d)15Correct answer is option 'D'. Can you explain this answer?, a detailed solution for What is the number of instantaneous centres of rotation for a 6-link mechanism?a)4b)6c)12d)15Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of What is the number of instantaneous centres of rotation for a 6-link mechanism?a)4b)6c)12d)15Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice What is the number of instantaneous centres of rotation for a 6-link mechanism?a)4b)6c)12d)15Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice SSC tests.
|
|
Explore Courses for SSC exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup