Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Questions > Let T be a depth first search tree in an undi...
Start Learning for Free
Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?
- a)There must exist a vertex w adjacent to both u and n in G
- b)There must exist a vertex w whose removal disconnects u and n in G
- c)There must exist a cycle in G containing u and n
- d)There must exist a cycle in G containing u and all its neighbours in G.
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
Let T be a depth first search tree in an undirected graph G. Vertices ...
Below example shows that A and B are FALSE:
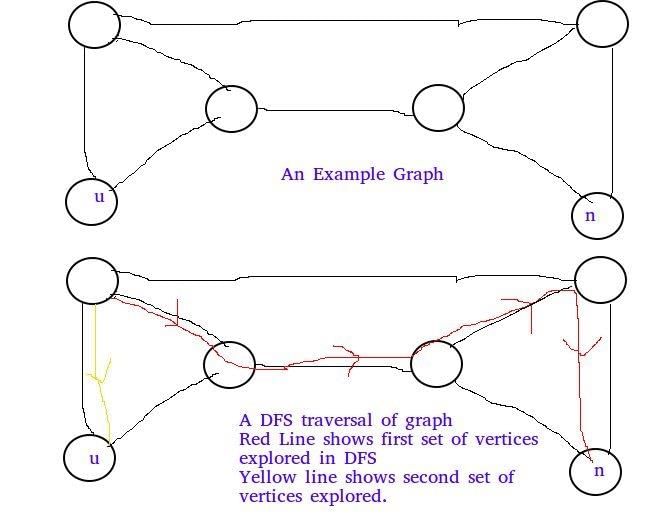
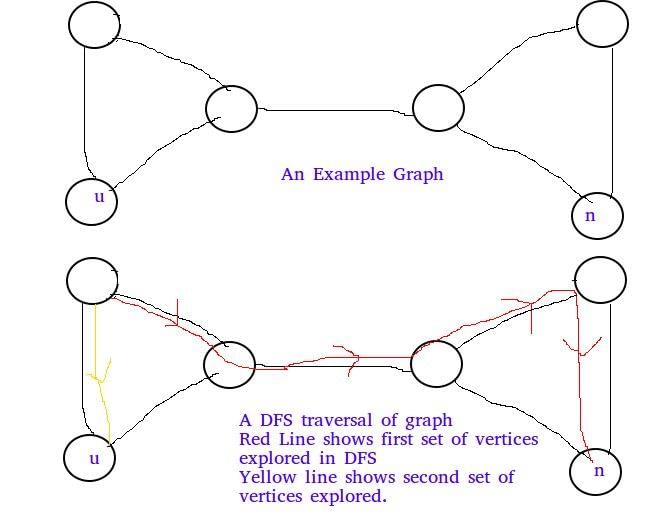
Below example shows C is false:
Most Upvoted Answer
Let T be a depth first search tree in an undirected graph G. Vertices ...
Understanding the Depth First Search Tree
In a depth first search (DFS) tree T, leaves represent vertices that have no children in the tree. In this case, both u and n are leaves, meaning that they were the last vertices visited in their respective branches of the DFS.
Vertex Degrees and Implications
- Both u and n have degrees of at least 2 in the original graph G.
- This implies that there are at least two edges connected to each vertex, allowing u and n to connect to other vertices apart from those in the DFS tree.
Analyzing the Statements
- Statement A: "There must exist a vertex w adjacent to both u and n in G."
- Not necessarily true as u and n could connect to completely different sets of vertices.
- Statement B: "There must exist a vertex w whose removal disconnects u and n in G."
- This is also not guaranteed. The removal of a single vertex does not ensure disconnection.
- Statement C: "There must exist a cycle in G containing u and n."
- While possible, it is not guaranteed as they may be connected differently.
- Statement D: "There must exist a cycle in G containing u and all its neighbors in G."
- Correct Statement: Since u is a leaf in the DFS tree but has a degree of at least 2, it must connect to other vertices. These neighbors can potentially connect to each other or n, forming a cycle.
Conclusion
Thus, the existence of a cycle involving u and all its neighbors is ensured by their connections, validating option D as the correct answer.
In a depth first search (DFS) tree T, leaves represent vertices that have no children in the tree. In this case, both u and n are leaves, meaning that they were the last vertices visited in their respective branches of the DFS.
Vertex Degrees and Implications
- Both u and n have degrees of at least 2 in the original graph G.
- This implies that there are at least two edges connected to each vertex, allowing u and n to connect to other vertices apart from those in the DFS tree.
Analyzing the Statements
- Statement A: "There must exist a vertex w adjacent to both u and n in G."
- Not necessarily true as u and n could connect to completely different sets of vertices.
- Statement B: "There must exist a vertex w whose removal disconnects u and n in G."
- This is also not guaranteed. The removal of a single vertex does not ensure disconnection.
- Statement C: "There must exist a cycle in G containing u and n."
- While possible, it is not guaranteed as they may be connected differently.
- Statement D: "There must exist a cycle in G containing u and all its neighbors in G."
- Correct Statement: Since u is a leaf in the DFS tree but has a degree of at least 2, it must connect to other vertices. These neighbors can potentially connect to each other or n, forming a cycle.
Conclusion
Thus, the existence of a cycle involving u and all its neighbors is ensured by their connections, validating option D as the correct answer.
Free Test
FREE
| Start Free Test |
Community Answer
Let T be a depth first search tree in an undirected graph G. Vertices ...
Below example shows that A and B are FALSE:

Below example shows C is false:


|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Question Description
Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?a)There must exist a vertex w adjacent to both u and n in Gb)There must exist a vertex w whose removal disconnects u and n in Gc)There must exist a cycle in G containing u and nd)There must exist a cycle in G containing u and all its neighbours in G.Correct answer is option 'D'. Can you explain this answer? for Computer Science Engineering (CSE) 2025 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?a)There must exist a vertex w adjacent to both u and n in Gb)There must exist a vertex w whose removal disconnects u and n in Gc)There must exist a cycle in G containing u and nd)There must exist a cycle in G containing u and all its neighbours in G.Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?a)There must exist a vertex w adjacent to both u and n in Gb)There must exist a vertex w whose removal disconnects u and n in Gc)There must exist a cycle in G containing u and nd)There must exist a cycle in G containing u and all its neighbours in G.Correct answer is option 'D'. Can you explain this answer?.
Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?a)There must exist a vertex w adjacent to both u and n in Gb)There must exist a vertex w whose removal disconnects u and n in Gc)There must exist a cycle in G containing u and nd)There must exist a cycle in G containing u and all its neighbours in G.Correct answer is option 'D'. Can you explain this answer? for Computer Science Engineering (CSE) 2025 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?a)There must exist a vertex w adjacent to both u and n in Gb)There must exist a vertex w whose removal disconnects u and n in Gc)There must exist a cycle in G containing u and nd)There must exist a cycle in G containing u and all its neighbours in G.Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?a)There must exist a vertex w adjacent to both u and n in Gb)There must exist a vertex w whose removal disconnects u and n in Gc)There must exist a cycle in G containing u and nd)There must exist a cycle in G containing u and all its neighbours in G.Correct answer is option 'D'. Can you explain this answer?.
Solutions for Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?a)There must exist a vertex w adjacent to both u and n in Gb)There must exist a vertex w whose removal disconnects u and n in Gc)There must exist a cycle in G containing u and nd)There must exist a cycle in G containing u and all its neighbours in G.Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Computer Science Engineering (CSE).
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Here you can find the meaning of Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?a)There must exist a vertex w adjacent to both u and n in Gb)There must exist a vertex w whose removal disconnects u and n in Gc)There must exist a cycle in G containing u and nd)There must exist a cycle in G containing u and all its neighbours in G.Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?a)There must exist a vertex w adjacent to both u and n in Gb)There must exist a vertex w whose removal disconnects u and n in Gc)There must exist a cycle in G containing u and nd)There must exist a cycle in G containing u and all its neighbours in G.Correct answer is option 'D'. Can you explain this answer?, a detailed solution for Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?a)There must exist a vertex w adjacent to both u and n in Gb)There must exist a vertex w whose removal disconnects u and n in Gc)There must exist a cycle in G containing u and nd)There must exist a cycle in G containing u and all its neighbours in G.Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?a)There must exist a vertex w adjacent to both u and n in Gb)There must exist a vertex w whose removal disconnects u and n in Gc)There must exist a cycle in G containing u and nd)There must exist a cycle in G containing u and all its neighbours in G.Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?a)There must exist a vertex w adjacent to both u and n in Gb)There must exist a vertex w whose removal disconnects u and n in Gc)There must exist a cycle in G containing u and nd)There must exist a cycle in G containing u and all its neighbours in G.Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice Computer Science Engineering (CSE) tests.

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















