SSC Exam > SSC Questions > A resistive load is to be impedance matched...
Start Learning for Free
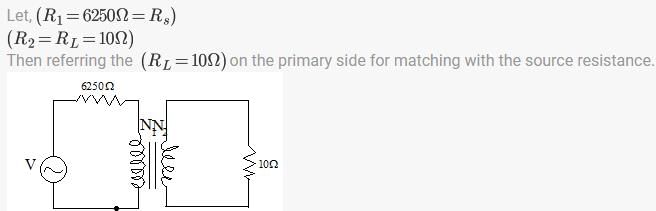
A resistive load is to be impedance matched by a transformer to a source with of internal resistance. The ratio of primary to secondary turns of the transformer should be-
- a)25
- b)10
- c)15
- d)20
Correct answer is option 'A'. Can you explain this answer?
Most Upvoted Answer
A resistive load is to be impedance matched by a transformer to a so...
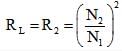
Free Test
FREE
| Start Free Test |
Community Answer
A resistive load is to be impedance matched by a transformer to a so...
To impedance match a resistive load to a source with internal resistance using a transformer, the turns ratio of the transformer needs to be determined. The turns ratio is the ratio of the number of turns in the primary winding of the transformer to the number of turns in the secondary winding.
To understand why the answer is option 'A' (25), we need to consider the concept of impedance matching and the relationship between impedance, resistance, and turns ratio in a transformer.
Impedance Matching:
Impedance matching is the process of adjusting the impedance of the load to match the impedance of the source. When the load impedance is matched to the source impedance, maximum power transfer occurs, resulting in efficient energy transfer.
Transformers and Turns Ratio:
A transformer is a device that transfers electrical energy between two or more circuits through electromagnetic induction. It consists of two windings, namely the primary winding and the secondary winding.
The turns ratio of a transformer is defined as the ratio of the number of turns in the primary winding (Np) to the number of turns in the secondary winding (Ns). It determines the voltage transformation ratio between the primary and secondary sides of the transformer.
Relationship between Impedance, Resistance, and Turns Ratio:
The impedance of a resistive load is purely resistive and can be represented as Z_load = R_load, where R_load is the load resistance. The impedance of the source with internal resistance can be represented as Z_source = R_source.
The impedance transformation ratio (K) of a transformer is given by the square of the turns ratio (K = (Np/Ns)^2). The impedance transformation ratio relates the primary impedance (Zp) to the secondary impedance (Zs) of the transformer.
In this case, we want to impedance match the resistive load to the source with internal resistance. To achieve impedance matching, the load impedance should be equal to the source impedance.
Explanation:
Since the load impedance is purely resistive, we can equate the load resistance (R_load) to the source resistance (R_source). Therefore, R_load = R_source.
The impedance transformation ratio (K) is given by K = (Np/Ns)^2.
To achieve impedance matching, we need to make the load impedance equal to the source impedance. Therefore, we can equate the load resistance to the source resistance: R_load = R_source.
From the above equations, we can deduce that (Np/Ns)^2 = R_load/R_source.
Since the load resistance and the source resistance are equal (R_load = R_source), the turns ratio squared is equal to 1: (Np/Ns)^2 = 1.
The only option among the given choices where the turns ratio squared is equal to 1 is option 'A' (25), as 5^2 = 25.
Therefore, the correct answer is option 'A' (25) for the ratio of primary to secondary turns of the transformer to impedance match a resistive load to a source with internal resistance.
To understand why the answer is option 'A' (25), we need to consider the concept of impedance matching and the relationship between impedance, resistance, and turns ratio in a transformer.
Impedance Matching:
Impedance matching is the process of adjusting the impedance of the load to match the impedance of the source. When the load impedance is matched to the source impedance, maximum power transfer occurs, resulting in efficient energy transfer.
Transformers and Turns Ratio:
A transformer is a device that transfers electrical energy between two or more circuits through electromagnetic induction. It consists of two windings, namely the primary winding and the secondary winding.
The turns ratio of a transformer is defined as the ratio of the number of turns in the primary winding (Np) to the number of turns in the secondary winding (Ns). It determines the voltage transformation ratio between the primary and secondary sides of the transformer.
Relationship between Impedance, Resistance, and Turns Ratio:
The impedance of a resistive load is purely resistive and can be represented as Z_load = R_load, where R_load is the load resistance. The impedance of the source with internal resistance can be represented as Z_source = R_source.
The impedance transformation ratio (K) of a transformer is given by the square of the turns ratio (K = (Np/Ns)^2). The impedance transformation ratio relates the primary impedance (Zp) to the secondary impedance (Zs) of the transformer.
In this case, we want to impedance match the resistive load to the source with internal resistance. To achieve impedance matching, the load impedance should be equal to the source impedance.
Explanation:
Since the load impedance is purely resistive, we can equate the load resistance (R_load) to the source resistance (R_source). Therefore, R_load = R_source.
The impedance transformation ratio (K) is given by K = (Np/Ns)^2.
To achieve impedance matching, we need to make the load impedance equal to the source impedance. Therefore, we can equate the load resistance to the source resistance: R_load = R_source.
From the above equations, we can deduce that (Np/Ns)^2 = R_load/R_source.
Since the load resistance and the source resistance are equal (R_load = R_source), the turns ratio squared is equal to 1: (Np/Ns)^2 = 1.
The only option among the given choices where the turns ratio squared is equal to 1 is option 'A' (25), as 5^2 = 25.
Therefore, the correct answer is option 'A' (25) for the ratio of primary to secondary turns of the transformer to impedance match a resistive load to a source with internal resistance.

|
Explore Courses for SSC exam
|

|
Similar SSC Doubts
Question Description
A resistive load is to be impedance matched by a transformer to a source with of internal resistance. The ratio of primary to secondary turns of the transformer should be-a)25b)10c)15d)20Correct answer is option 'A'. Can you explain this answer? for SSC 2025 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about A resistive load is to be impedance matched by a transformer to a source with of internal resistance. The ratio of primary to secondary turns of the transformer should be-a)25b)10c)15d)20Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for SSC 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A resistive load is to be impedance matched by a transformer to a source with of internal resistance. The ratio of primary to secondary turns of the transformer should be-a)25b)10c)15d)20Correct answer is option 'A'. Can you explain this answer?.
A resistive load is to be impedance matched by a transformer to a source with of internal resistance. The ratio of primary to secondary turns of the transformer should be-a)25b)10c)15d)20Correct answer is option 'A'. Can you explain this answer? for SSC 2025 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about A resistive load is to be impedance matched by a transformer to a source with of internal resistance. The ratio of primary to secondary turns of the transformer should be-a)25b)10c)15d)20Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for SSC 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A resistive load is to be impedance matched by a transformer to a source with of internal resistance. The ratio of primary to secondary turns of the transformer should be-a)25b)10c)15d)20Correct answer is option 'A'. Can you explain this answer?.
Solutions for A resistive load is to be impedance matched by a transformer to a source with of internal resistance. The ratio of primary to secondary turns of the transformer should be-a)25b)10c)15d)20Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for SSC.
Download more important topics, notes, lectures and mock test series for SSC Exam by signing up for free.
Here you can find the meaning of A resistive load is to be impedance matched by a transformer to a source with of internal resistance. The ratio of primary to secondary turns of the transformer should be-a)25b)10c)15d)20Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A resistive load is to be impedance matched by a transformer to a source with of internal resistance. The ratio of primary to secondary turns of the transformer should be-a)25b)10c)15d)20Correct answer is option 'A'. Can you explain this answer?, a detailed solution for A resistive load is to be impedance matched by a transformer to a source with of internal resistance. The ratio of primary to secondary turns of the transformer should be-a)25b)10c)15d)20Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of A resistive load is to be impedance matched by a transformer to a source with of internal resistance. The ratio of primary to secondary turns of the transformer should be-a)25b)10c)15d)20Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A resistive load is to be impedance matched by a transformer to a source with of internal resistance. The ratio of primary to secondary turns of the transformer should be-a)25b)10c)15d)20Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice SSC tests.

|
Explore Courses for SSC exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.















