Railways Exam > Railways Questions > An unbounded solution of linear programming ...
Start Learning for Free
An unbounded solution of linear programming problem is reflected in the simplex method, when
- a)All the ratio of ‘right hand sides’ to coefficients in key column become negative
- b)All the ratios of right hand sides to coefficients in key columns become zero
- c)All right hand sides become negative
- d)All right hand become zero
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
An unbounded solution of linear programming problem is reflected in t...
Unbounded Solution : If the feasible region is not bounded, it is possible that the value of the objective function goes on increasing without leaving the feasible region. This is known as an unbounded solution.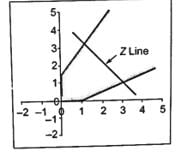
View all questions of this test

Most Upvoted Answer
An unbounded solution of linear programming problem is reflected in t...
Explanation:
The simplex method is an iterative algorithm used to solve linear programming problems. It starts with an initial feasible solution and then iteratively improves it until an optimal solution is reached. In each iteration, the simplex method selects a pivot element to enter and leave the basis, which results in a new feasible solution.
An unbounded solution in linear programming occurs when the objective function can be made arbitrarily large or small without violating any of the constraints. This means that there is no finite optimal solution, and the objective function value can be increased or decreased indefinitely.
Simplex Method and Unbounded Solution:
In the simplex method, the selection of the pivot element is based on the ratios of the right-hand sides (RHS) to the coefficients in the key column. The key column represents the coefficients of the basic variables in the current basis.
If all the ratios of the RHS to the coefficients in the key column become negative, it indicates that the objective function can be made arbitrarily small (negative) without violating any of the constraints. This implies an unbounded solution because there is no finite optimal solution, and the objective function value can be decreased indefinitely.
The simplex method detects this unboundedness and terminates, indicating that the problem is unbounded. It means that the constraints are not sufficiently restrictive to limit the objective function value.
Other Options:
The other options mentioned in the question are not correct:
- If all the ratios of the RHS to the coefficients in the key column become zero, it means that the objective function cannot be increased or decreased. This indicates a degenerate solution, not an unbounded solution.
- If all the right-hand sides become negative, it does not necessarily indicate an unbounded solution. It means that all the constraints are violated, and there is no feasible solution.
- If all the right-hand sides become zero, it indicates a degenerate solution, not an unbounded solution.
Therefore, the correct answer is option 'A', where all the ratios of the RHS to the coefficients in the key column become negative. This reflects an unbounded solution in the simplex method.
The simplex method is an iterative algorithm used to solve linear programming problems. It starts with an initial feasible solution and then iteratively improves it until an optimal solution is reached. In each iteration, the simplex method selects a pivot element to enter and leave the basis, which results in a new feasible solution.
An unbounded solution in linear programming occurs when the objective function can be made arbitrarily large or small without violating any of the constraints. This means that there is no finite optimal solution, and the objective function value can be increased or decreased indefinitely.
Simplex Method and Unbounded Solution:
In the simplex method, the selection of the pivot element is based on the ratios of the right-hand sides (RHS) to the coefficients in the key column. The key column represents the coefficients of the basic variables in the current basis.
If all the ratios of the RHS to the coefficients in the key column become negative, it indicates that the objective function can be made arbitrarily small (negative) without violating any of the constraints. This implies an unbounded solution because there is no finite optimal solution, and the objective function value can be decreased indefinitely.
The simplex method detects this unboundedness and terminates, indicating that the problem is unbounded. It means that the constraints are not sufficiently restrictive to limit the objective function value.
Other Options:
The other options mentioned in the question are not correct:
- If all the ratios of the RHS to the coefficients in the key column become zero, it means that the objective function cannot be increased or decreased. This indicates a degenerate solution, not an unbounded solution.
- If all the right-hand sides become negative, it does not necessarily indicate an unbounded solution. It means that all the constraints are violated, and there is no feasible solution.
- If all the right-hand sides become zero, it indicates a degenerate solution, not an unbounded solution.
Therefore, the correct answer is option 'A', where all the ratios of the RHS to the coefficients in the key column become negative. This reflects an unbounded solution in the simplex method.
Attention Railways Students!
To make sure you are not studying endlessly, EduRev has designed Railways study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Railways.

|
Explore Courses for Railways exam
|

|
Similar Railways Doubts
An unbounded solution of linear programming problem is reflected in the simplex method, whena)All the ratio of ‘right hand sides’ to coefficients in key column become negativeb)All the ratios of right hand sides to coefficients in key columns become zeroc)All right hand sides become negatived)All right hand become zeroCorrect answer is option 'A'. Can you explain this answer?
Question Description
An unbounded solution of linear programming problem is reflected in the simplex method, whena)All the ratio of ‘right hand sides’ to coefficients in key column become negativeb)All the ratios of right hand sides to coefficients in key columns become zeroc)All right hand sides become negatived)All right hand become zeroCorrect answer is option 'A'. Can you explain this answer? for Railways 2024 is part of Railways preparation. The Question and answers have been prepared according to the Railways exam syllabus. Information about An unbounded solution of linear programming problem is reflected in the simplex method, whena)All the ratio of ‘right hand sides’ to coefficients in key column become negativeb)All the ratios of right hand sides to coefficients in key columns become zeroc)All right hand sides become negatived)All right hand become zeroCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Railways 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An unbounded solution of linear programming problem is reflected in the simplex method, whena)All the ratio of ‘right hand sides’ to coefficients in key column become negativeb)All the ratios of right hand sides to coefficients in key columns become zeroc)All right hand sides become negatived)All right hand become zeroCorrect answer is option 'A'. Can you explain this answer?.
An unbounded solution of linear programming problem is reflected in the simplex method, whena)All the ratio of ‘right hand sides’ to coefficients in key column become negativeb)All the ratios of right hand sides to coefficients in key columns become zeroc)All right hand sides become negatived)All right hand become zeroCorrect answer is option 'A'. Can you explain this answer? for Railways 2024 is part of Railways preparation. The Question and answers have been prepared according to the Railways exam syllabus. Information about An unbounded solution of linear programming problem is reflected in the simplex method, whena)All the ratio of ‘right hand sides’ to coefficients in key column become negativeb)All the ratios of right hand sides to coefficients in key columns become zeroc)All right hand sides become negatived)All right hand become zeroCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Railways 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An unbounded solution of linear programming problem is reflected in the simplex method, whena)All the ratio of ‘right hand sides’ to coefficients in key column become negativeb)All the ratios of right hand sides to coefficients in key columns become zeroc)All right hand sides become negatived)All right hand become zeroCorrect answer is option 'A'. Can you explain this answer?.
Solutions for An unbounded solution of linear programming problem is reflected in the simplex method, whena)All the ratio of ‘right hand sides’ to coefficients in key column become negativeb)All the ratios of right hand sides to coefficients in key columns become zeroc)All right hand sides become negatived)All right hand become zeroCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Railways.
Download more important topics, notes, lectures and mock test series for Railways Exam by signing up for free.
Here you can find the meaning of An unbounded solution of linear programming problem is reflected in the simplex method, whena)All the ratio of ‘right hand sides’ to coefficients in key column become negativeb)All the ratios of right hand sides to coefficients in key columns become zeroc)All right hand sides become negatived)All right hand become zeroCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
An unbounded solution of linear programming problem is reflected in the simplex method, whena)All the ratio of ‘right hand sides’ to coefficients in key column become negativeb)All the ratios of right hand sides to coefficients in key columns become zeroc)All right hand sides become negatived)All right hand become zeroCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for An unbounded solution of linear programming problem is reflected in the simplex method, whena)All the ratio of ‘right hand sides’ to coefficients in key column become negativeb)All the ratios of right hand sides to coefficients in key columns become zeroc)All right hand sides become negatived)All right hand become zeroCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of An unbounded solution of linear programming problem is reflected in the simplex method, whena)All the ratio of ‘right hand sides’ to coefficients in key column become negativeb)All the ratios of right hand sides to coefficients in key columns become zeroc)All right hand sides become negatived)All right hand become zeroCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice An unbounded solution of linear programming problem is reflected in the simplex method, whena)All the ratio of ‘right hand sides’ to coefficients in key column become negativeb)All the ratios of right hand sides to coefficients in key columns become zeroc)All right hand sides become negatived)All right hand become zeroCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Railways tests.

|
Explore Courses for Railways exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























