GATE Exam > GATE Questions > Determine the distance from the pipe wall at ...
Start Learning for Free
Determine the distance from the pipe wall at which local velocity is equal to the average velocity for turbulent flow in pipe
- a)0.2807 R
- b)0.7070 R
- c)0.1414 R
- d)0.2228 R
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
Determine the distance from the pipe wall at which local velocity is e...
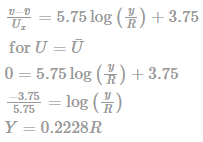
Most Upvoted Answer
Determine the distance from the pipe wall at which local velocity is e...
Introduction:
The question asks us to determine the distance from the pipe wall at which the local velocity is equal to the average velocity for turbulent flow in a pipe. Turbulent flow is characterized by chaotic and irregular motion of fluid particles.
Explanation:
To solve this problem, we need to understand the concept of turbulent flow and its velocity profile in a pipe.
Turbulent Flow:
Turbulent flow is a type of fluid flow where the velocity of the fluid particles varies chaotically in both magnitude and direction. In a pipe, turbulent flow occurs at high Reynolds numbers (Re > 4000), which is a dimensionless parameter that characterizes the flow regime.
Velocity Profile in Turbulent Flow:
In turbulent flow, the velocity profile across the pipe is not a simple parabolic shape like in laminar flow. Instead, it has a more flattened profile with higher velocities near the center of the pipe and lower velocities near the pipe walls.
Distance from Pipe Wall:
The distance from the pipe wall at which the local velocity is equal to the average velocity can be determined using the concept of the velocity profile in turbulent flow.
The average velocity in a pipe can be calculated using the equation:
Average Velocity = (Maximum Velocity + Minimum Velocity) / 2
In turbulent flow, the maximum velocity occurs at the center of the pipe, while the minimum velocity occurs at the pipe wall. Therefore, the average velocity lies somewhere between the maximum and minimum velocities.
To find the distance from the pipe wall at which the local velocity is equal to the average velocity, we need to determine the location where the velocity profile intersects the average velocity.
Solution:
The correct answer is option 'D' (0.2228 R). This means that the distance from the pipe wall at which the local velocity is equal to the average velocity is approximately 0.2228 times the pipe radius (R).
This value is obtained by analyzing the velocity profile in turbulent flow and finding the location where the local velocity equals the average velocity. The specific calculations for this value are not provided in the question, but it can be determined using experimental data or computational fluid dynamics (CFD) simulations.
Summary:
In summary, the distance from the pipe wall at which the local velocity is equal to the average velocity in turbulent flow is approximately 0.2228 times the pipe radius. This value is obtained by analyzing the velocity profile in turbulent flow and finding the location where the local velocity equals the average velocity.
The question asks us to determine the distance from the pipe wall at which the local velocity is equal to the average velocity for turbulent flow in a pipe. Turbulent flow is characterized by chaotic and irregular motion of fluid particles.
Explanation:
To solve this problem, we need to understand the concept of turbulent flow and its velocity profile in a pipe.
Turbulent Flow:
Turbulent flow is a type of fluid flow where the velocity of the fluid particles varies chaotically in both magnitude and direction. In a pipe, turbulent flow occurs at high Reynolds numbers (Re > 4000), which is a dimensionless parameter that characterizes the flow regime.
Velocity Profile in Turbulent Flow:
In turbulent flow, the velocity profile across the pipe is not a simple parabolic shape like in laminar flow. Instead, it has a more flattened profile with higher velocities near the center of the pipe and lower velocities near the pipe walls.
Distance from Pipe Wall:
The distance from the pipe wall at which the local velocity is equal to the average velocity can be determined using the concept of the velocity profile in turbulent flow.
The average velocity in a pipe can be calculated using the equation:
Average Velocity = (Maximum Velocity + Minimum Velocity) / 2
In turbulent flow, the maximum velocity occurs at the center of the pipe, while the minimum velocity occurs at the pipe wall. Therefore, the average velocity lies somewhere between the maximum and minimum velocities.
To find the distance from the pipe wall at which the local velocity is equal to the average velocity, we need to determine the location where the velocity profile intersects the average velocity.
Solution:
The correct answer is option 'D' (0.2228 R). This means that the distance from the pipe wall at which the local velocity is equal to the average velocity is approximately 0.2228 times the pipe radius (R).
This value is obtained by analyzing the velocity profile in turbulent flow and finding the location where the local velocity equals the average velocity. The specific calculations for this value are not provided in the question, but it can be determined using experimental data or computational fluid dynamics (CFD) simulations.
Summary:
In summary, the distance from the pipe wall at which the local velocity is equal to the average velocity in turbulent flow is approximately 0.2228 times the pipe radius. This value is obtained by analyzing the velocity profile in turbulent flow and finding the location where the local velocity equals the average velocity.
Free Test
FREE
| Start Free Test |
Community Answer
Determine the distance from the pipe wall at which local velocity is e...
D)0.2228 R

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
Question Description
Determine the distance from the pipe wall at which local velocity is equal to the average velocity for turbulent flow in pipea)0.2807 Rb)0.7070 Rc)0.1414 Rd)0.2228 RCorrect answer is option 'D'. Can you explain this answer? for GATE 2025 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Determine the distance from the pipe wall at which local velocity is equal to the average velocity for turbulent flow in pipea)0.2807 Rb)0.7070 Rc)0.1414 Rd)0.2228 RCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for GATE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Determine the distance from the pipe wall at which local velocity is equal to the average velocity for turbulent flow in pipea)0.2807 Rb)0.7070 Rc)0.1414 Rd)0.2228 RCorrect answer is option 'D'. Can you explain this answer?.
Determine the distance from the pipe wall at which local velocity is equal to the average velocity for turbulent flow in pipea)0.2807 Rb)0.7070 Rc)0.1414 Rd)0.2228 RCorrect answer is option 'D'. Can you explain this answer? for GATE 2025 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Determine the distance from the pipe wall at which local velocity is equal to the average velocity for turbulent flow in pipea)0.2807 Rb)0.7070 Rc)0.1414 Rd)0.2228 RCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for GATE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Determine the distance from the pipe wall at which local velocity is equal to the average velocity for turbulent flow in pipea)0.2807 Rb)0.7070 Rc)0.1414 Rd)0.2228 RCorrect answer is option 'D'. Can you explain this answer?.
Solutions for Determine the distance from the pipe wall at which local velocity is equal to the average velocity for turbulent flow in pipea)0.2807 Rb)0.7070 Rc)0.1414 Rd)0.2228 RCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of Determine the distance from the pipe wall at which local velocity is equal to the average velocity for turbulent flow in pipea)0.2807 Rb)0.7070 Rc)0.1414 Rd)0.2228 RCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Determine the distance from the pipe wall at which local velocity is equal to the average velocity for turbulent flow in pipea)0.2807 Rb)0.7070 Rc)0.1414 Rd)0.2228 RCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for Determine the distance from the pipe wall at which local velocity is equal to the average velocity for turbulent flow in pipea)0.2807 Rb)0.7070 Rc)0.1414 Rd)0.2228 RCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of Determine the distance from the pipe wall at which local velocity is equal to the average velocity for turbulent flow in pipea)0.2807 Rb)0.7070 Rc)0.1414 Rd)0.2228 RCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Determine the distance from the pipe wall at which local velocity is equal to the average velocity for turbulent flow in pipea)0.2807 Rb)0.7070 Rc)0.1414 Rd)0.2228 RCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.




















