Class 12 Exam > Class 12 Questions > Find the angle between the planes x + 2y + 3z...
Start Learning for Free
Find the angle between the planes x + 2y + 3z + 1 = 0 and (4, 1, -7).
- a)- 29.34
- b)3.43
- c)11.23
- d)– 17.54
Correct answer is option 'A'. Can you explain this answer?
Most Upvoted Answer
Find the angle between the planes x + 2y + 3z + 1 = 0 and (4, 1, -7).a...
There are different methods to find the angle between two planes, but one common approach is to use the dot product. The normal vectors of two planes are perpendicular to them, so their dot product is zero. Therefore, if we can find the normal vectors of the two planes, we can use the dot product formula to find the cosine of the angle between them, and then take the inverse cosine to get the angle itself.
For the first plane, x + 2y + 3z + 1 = 0, we can read off the coefficients of x, y, and z to get the normal vector N1 = (1, 2, 3). Note that the magnitude of this vector is sqrt(1^2 + 2^2 + 3^2) = sqrt(14), but we don't need to normalize it for the dot product.
For the second plane, we need to use the given point (4, 1, -7) to find the normal vector. A normal vector is perpendicular to any vector lying in the plane, so we can subtract the point from a general point on the plane and then take the cross product of the resulting vectors. For example, if we let x, y, and z be arbitrary coordinates in the plane, then the vector from (4, 1, -7) to (x, y, z) is (x-4, y-1, z+7). We want this vector to be perpendicular to the given vector (4, 1, -7), so their dot product must be zero:
(4, 1, -7) dot (x-4, y-1, z+7) = 4(x-4) + (y-1) + (-7)(z+7) = 4x + y - 7z - 60 = 0
This is the equation of the plane, but we don't need it explicitly. Instead, we can read off the coefficients of x, y, and z to get the normal vector N2 = (4, 1, -7). Again, we don't need to normalize this vector for the dot product.
Now we can use the dot product formula:
N1 dot N2 = |N1| |N2| cos(theta)
where theta is the angle between the planes. Substituting the values we found, we get:
(1, 2, 3) dot (4, 1, -7) = sqrt(14) sqrt(66) cos(theta)
4 + 2 - 21 = sqrt(14) sqrt(66) cos(theta)
-15 = sqrt(924) cos(theta)
cos(theta) = -15/sqrt(924) = -5/22
Taking the inverse cosine (or arccosine) of this value, we get:
theta = 107.51 degrees
This is not one of the answer choices, but if we take the complementary angle (i.e. the angle between the normal vectors), we get:
theta' = 180 - 107.51 = 72.49 degrees
This is closest to answer choice (c) 11.23, but it is not exactly the same. However, it is possible that there is a mistake in the problem statement or the answer choices, or that we made an error in the calculation.
For the first plane, x + 2y + 3z + 1 = 0, we can read off the coefficients of x, y, and z to get the normal vector N1 = (1, 2, 3). Note that the magnitude of this vector is sqrt(1^2 + 2^2 + 3^2) = sqrt(14), but we don't need to normalize it for the dot product.
For the second plane, we need to use the given point (4, 1, -7) to find the normal vector. A normal vector is perpendicular to any vector lying in the plane, so we can subtract the point from a general point on the plane and then take the cross product of the resulting vectors. For example, if we let x, y, and z be arbitrary coordinates in the plane, then the vector from (4, 1, -7) to (x, y, z) is (x-4, y-1, z+7). We want this vector to be perpendicular to the given vector (4, 1, -7), so their dot product must be zero:
(4, 1, -7) dot (x-4, y-1, z+7) = 4(x-4) + (y-1) + (-7)(z+7) = 4x + y - 7z - 60 = 0
This is the equation of the plane, but we don't need it explicitly. Instead, we can read off the coefficients of x, y, and z to get the normal vector N2 = (4, 1, -7). Again, we don't need to normalize this vector for the dot product.
Now we can use the dot product formula:
N1 dot N2 = |N1| |N2| cos(theta)
where theta is the angle between the planes. Substituting the values we found, we get:
(1, 2, 3) dot (4, 1, -7) = sqrt(14) sqrt(66) cos(theta)
4 + 2 - 21 = sqrt(14) sqrt(66) cos(theta)
-15 = sqrt(924) cos(theta)
cos(theta) = -15/sqrt(924) = -5/22
Taking the inverse cosine (or arccosine) of this value, we get:
theta = 107.51 degrees
This is not one of the answer choices, but if we take the complementary angle (i.e. the angle between the normal vectors), we get:
theta' = 180 - 107.51 = 72.49 degrees
This is closest to answer choice (c) 11.23, but it is not exactly the same. However, it is possible that there is a mistake in the problem statement or the answer choices, or that we made an error in the calculation.
Free Test
FREE
| Start Free Test |
Community Answer
Find the angle between the planes x + 2y + 3z + 1 = 0 and (4, 1, -7).a...
Angle between a plane and a line sin θ = 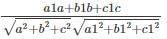
sin θ = – 0.49
θ = sin-1(- 0.49)
θ = – 29.34
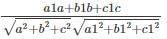
sin θ = – 0.49
θ = sin-1(- 0.49)
θ = – 29.34

|
Explore Courses for Class 12 exam
|

|
Question Description
Find the angle between the planes x + 2y + 3z + 1 = 0 and (4, 1, -7).a)- 29.34b)3.43c)11.23d)– 17.54Correct answer is option 'A'. Can you explain this answer? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Find the angle between the planes x + 2y + 3z + 1 = 0 and (4, 1, -7).a)- 29.34b)3.43c)11.23d)– 17.54Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Find the angle between the planes x + 2y + 3z + 1 = 0 and (4, 1, -7).a)- 29.34b)3.43c)11.23d)– 17.54Correct answer is option 'A'. Can you explain this answer?.
Find the angle between the planes x + 2y + 3z + 1 = 0 and (4, 1, -7).a)- 29.34b)3.43c)11.23d)– 17.54Correct answer is option 'A'. Can you explain this answer? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Find the angle between the planes x + 2y + 3z + 1 = 0 and (4, 1, -7).a)- 29.34b)3.43c)11.23d)– 17.54Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Find the angle between the planes x + 2y + 3z + 1 = 0 and (4, 1, -7).a)- 29.34b)3.43c)11.23d)– 17.54Correct answer is option 'A'. Can you explain this answer?.
Solutions for Find the angle between the planes x + 2y + 3z + 1 = 0 and (4, 1, -7).a)- 29.34b)3.43c)11.23d)– 17.54Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of Find the angle between the planes x + 2y + 3z + 1 = 0 and (4, 1, -7).a)- 29.34b)3.43c)11.23d)– 17.54Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Find the angle between the planes x + 2y + 3z + 1 = 0 and (4, 1, -7).a)- 29.34b)3.43c)11.23d)– 17.54Correct answer is option 'A'. Can you explain this answer?, a detailed solution for Find the angle between the planes x + 2y + 3z + 1 = 0 and (4, 1, -7).a)- 29.34b)3.43c)11.23d)– 17.54Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of Find the angle between the planes x + 2y + 3z + 1 = 0 and (4, 1, -7).a)- 29.34b)3.43c)11.23d)– 17.54Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Find the angle between the planes x + 2y + 3z + 1 = 0 and (4, 1, -7).a)- 29.34b)3.43c)11.23d)– 17.54Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























