Class 10 Exam > Class 10 Questions > Mathematical designs and patterns using arith...
Start Learning for Free
Mathematical designs and patterns using arithmetic progression
Most Upvoted Answer
Mathematical designs and patterns using arithmetic progression
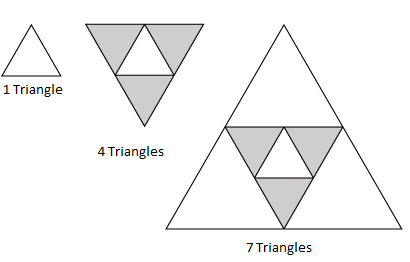
The given figure shows the number of triangles made with small triangles which are in A.P..
Similarly we can do the same for other shapes like square, circle etc.
Community Answer
Mathematical designs and patterns using arithmetic progression
Mathematical Designs and Patterns using Arithmetic Progression
Arithmetic progression (AP) is a sequence of numbers in which the difference between any two consecutive terms is constant. These sequences are widely used in mathematics, physics, computer science, and various other fields. They have interesting patterns and designs that can be explored and analyzed. Let's delve into some of these patterns and designs using arithmetic progression.
1. Basic Arithmetic Progression:
- Arithmetic progression is denoted by the formula: a, a + d, a + 2d, a + 3d, ...
- 'a' represents the first term, and 'd' is the common difference.
- The common difference determines the pattern in an arithmetic progression.
2. Linear Growth and Decay:
- Arithmetic progressions can model linear growth or decay scenarios.
- If the common difference 'd' is positive, the sequence increases, representing growth.
- If 'd' is negative, the sequence decreases, representing decay.
3. Number Patterns:
- Arithmetic progressions exhibit various number patterns.
- For example, consider an arithmetic progression with a first term 'a' and a common difference 'd'.
- The sum of the first 'n' terms in an arithmetic progression can be calculated using the formula: Sn = (n/2)(2a + (n-1)d).
- This formula helps identify patterns in the sum of terms.
4. Visual Patterns:
- Arithmetic progressions can be visually appealing when represented graphically.
- Plotting the terms of an arithmetic progression on a graph generates a straight line.
- The slope of the line corresponds to the common difference 'd'.
5. Applications:
- Arithmetic progressions have numerous applications in real-life scenarios.
- They are used in financial calculations, such as calculating compound interest.
- They are also used in physics to model motion, where the position of an object changes linearly over time.
- In computer science, arithmetic progressions are used to optimize algorithms and solve problems efficiently.
Conclusion:
Arithmetic progressions provide a mathematical framework to understand and analyze patterns and designs. They represent various real-life scenarios and can be used to model linear growth or decay. By exploring the number patterns, visual representations, and real-life applications, we can appreciate the significance of arithmetic progressions in different fields.
Arithmetic progression (AP) is a sequence of numbers in which the difference between any two consecutive terms is constant. These sequences are widely used in mathematics, physics, computer science, and various other fields. They have interesting patterns and designs that can be explored and analyzed. Let's delve into some of these patterns and designs using arithmetic progression.
1. Basic Arithmetic Progression:
- Arithmetic progression is denoted by the formula: a, a + d, a + 2d, a + 3d, ...
- 'a' represents the first term, and 'd' is the common difference.
- The common difference determines the pattern in an arithmetic progression.
2. Linear Growth and Decay:
- Arithmetic progressions can model linear growth or decay scenarios.
- If the common difference 'd' is positive, the sequence increases, representing growth.
- If 'd' is negative, the sequence decreases, representing decay.
3. Number Patterns:
- Arithmetic progressions exhibit various number patterns.
- For example, consider an arithmetic progression with a first term 'a' and a common difference 'd'.
- The sum of the first 'n' terms in an arithmetic progression can be calculated using the formula: Sn = (n/2)(2a + (n-1)d).
- This formula helps identify patterns in the sum of terms.
4. Visual Patterns:
- Arithmetic progressions can be visually appealing when represented graphically.
- Plotting the terms of an arithmetic progression on a graph generates a straight line.
- The slope of the line corresponds to the common difference 'd'.
5. Applications:
- Arithmetic progressions have numerous applications in real-life scenarios.
- They are used in financial calculations, such as calculating compound interest.
- They are also used in physics to model motion, where the position of an object changes linearly over time.
- In computer science, arithmetic progressions are used to optimize algorithms and solve problems efficiently.
Conclusion:
Arithmetic progressions provide a mathematical framework to understand and analyze patterns and designs. They represent various real-life scenarios and can be used to model linear growth or decay. By exploring the number patterns, visual representations, and real-life applications, we can appreciate the significance of arithmetic progressions in different fields.

|
Explore Courses for Class 10 exam
|

|
Question Description
Mathematical designs and patterns using arithmetic progression for Class 10 2025 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about Mathematical designs and patterns using arithmetic progression covers all topics & solutions for Class 10 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Mathematical designs and patterns using arithmetic progression.
Mathematical designs and patterns using arithmetic progression for Class 10 2025 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about Mathematical designs and patterns using arithmetic progression covers all topics & solutions for Class 10 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Mathematical designs and patterns using arithmetic progression.
Solutions for Mathematical designs and patterns using arithmetic progression in English & in Hindi are available as part of our courses for Class 10.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Here you can find the meaning of Mathematical designs and patterns using arithmetic progression defined & explained in the simplest way possible. Besides giving the explanation of
Mathematical designs and patterns using arithmetic progression, a detailed solution for Mathematical designs and patterns using arithmetic progression has been provided alongside types of Mathematical designs and patterns using arithmetic progression theory, EduRev gives you an
ample number of questions to practice Mathematical designs and patterns using arithmetic progression tests, examples and also practice Class 10 tests.

|
Explore Courses for Class 10 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















