Electrical Engineering (EE) Exam > Electrical Engineering (EE) Questions > Three currents i1, i2, and i3meet at a node. ...
Start Learning for Free
Three currents i1, i2, and i3 meet at a node. if i1 = 10 sin (400t + 60°) A, and i2 = 10sin (400t - 60°) A then i3 =
- a)0
- b)10sin 400t A
- c)-10sin 400t A
- d)-5 √3 sin 400t
Correct answer is option 'C'. Can you explain this answer?
Most Upvoted Answer
Three currents i1, i2, and i3meet at a node. ifi1= 10 sin (400t + 60&d...
Given Information:
The currents i1 and i2 are given as:
i1 = 10 sin (400t + 60°) A
i2 = 10 sin (400t - 60°) A
Calculating i3:
At the node where the currents i1, i2, and i3 meet, the algebraic sum of currents is zero. Therefore, we can write the equation as:
i1 + i2 + i3 = 0
Substitute the given values of i1 and i2 into the equation:
10 sin (400t + 60°) + 10 sin (400t - 60°) + i3 = 0
Simplify the equation by using the trigonometric identity:
sin (A + B) + sin (A - B) = 2 sin A cos B
10 [sin 400t cos 60° + cos 400t sin 60°] + i3 = 0
10 [sin 400t * 0.5 + cos 400t * √3/2] + i3 = 0
5 sin 400t + 5√3 cos 400t + i3 = 0
Therefore, the current i3 is:
i3 = -5√3 sin 400t A
Conclusion:
The correct answer is option C, i.e., i3 = -5√3 sin 400t A. This is the current flowing in the third branch at the node where currents i1 and i2 meet.
The currents i1 and i2 are given as:
i1 = 10 sin (400t + 60°) A
i2 = 10 sin (400t - 60°) A
Calculating i3:
At the node where the currents i1, i2, and i3 meet, the algebraic sum of currents is zero. Therefore, we can write the equation as:
i1 + i2 + i3 = 0
Substitute the given values of i1 and i2 into the equation:
10 sin (400t + 60°) + 10 sin (400t - 60°) + i3 = 0
Simplify the equation by using the trigonometric identity:
sin (A + B) + sin (A - B) = 2 sin A cos B
10 [sin 400t cos 60° + cos 400t sin 60°] + i3 = 0
10 [sin 400t * 0.5 + cos 400t * √3/2] + i3 = 0
5 sin 400t + 5√3 cos 400t + i3 = 0
Therefore, the current i3 is:
i3 = -5√3 sin 400t A
Conclusion:
The correct answer is option C, i.e., i3 = -5√3 sin 400t A. This is the current flowing in the third branch at the node where currents i1 and i2 meet.
Free Test
FREE
| Start Free Test |
Community Answer
Three currents i1, i2, and i3meet at a node. ifi1= 10 sin (400t + 60&d...
Kirchhoff’s Current Law (KCL): It states that the algebraic sum of currents entering a node or closed boundary is zero.
Mathematically, KCL implies that
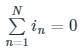
Where N is the number of branches connected to the node
And in is the nth current entering or leaving the node.
By this law current entering a node may be regarded as positive and current leaving a node may be regarded as negative or vice-versa.
Hence, the sum of currents entering a node is equal to the sum of the currents leaving the node.
Calculation:
Given that, three currents i1, i2, and i3 meet at a node,
From the above concept,
i1,+ i2, + i3 = 0
or, i3 = - (i1 + i2)
Since the current is given in phasor form, hence the addition of current i1 and i2 can be done by using the parallelogram method,
We have,
i1 = 10 sin (400t + 60°) A .... (1)
i2 = 10sin (400t - 60°) A .... (2)
The phasor diagram can be drawn as,
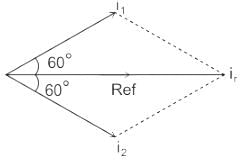
By using the parallelogram method,
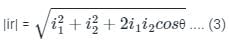
Where, it is the resultant current
We have, θ = (60° + 60°) = 120°
From equation (1), (2) & (3),
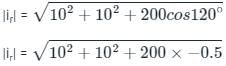
= 10
Since i1 & i2 has the same phase angle as well as the magnitude,
∴ ir = 10sin 400t A
Since the sum of all current is zero, hence,
i3 = - ir = - 10sin 400t A
|
Explore Courses for Electrical Engineering (EE) exam
|
|
Top Courses for Electrical Engineering (EE)View all
Question Description
Three currents i1, i2, and i3meet at a node. ifi1= 10 sin (400t + 60°) A, andi2= 10sin (400t - 60°) Athen i3=a)0b)10sin 400t Ac)-10sin 400t Ad)-5 √3 sin 400tCorrect answer is option 'C'. Can you explain this answer? for Electrical Engineering (EE) 2025 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about Three currents i1, i2, and i3meet at a node. ifi1= 10 sin (400t + 60°) A, andi2= 10sin (400t - 60°) Athen i3=a)0b)10sin 400t Ac)-10sin 400t Ad)-5 √3 sin 400tCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Three currents i1, i2, and i3meet at a node. ifi1= 10 sin (400t + 60°) A, andi2= 10sin (400t - 60°) Athen i3=a)0b)10sin 400t Ac)-10sin 400t Ad)-5 √3 sin 400tCorrect answer is option 'C'. Can you explain this answer?.
Three currents i1, i2, and i3meet at a node. ifi1= 10 sin (400t + 60°) A, andi2= 10sin (400t - 60°) Athen i3=a)0b)10sin 400t Ac)-10sin 400t Ad)-5 √3 sin 400tCorrect answer is option 'C'. Can you explain this answer? for Electrical Engineering (EE) 2025 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about Three currents i1, i2, and i3meet at a node. ifi1= 10 sin (400t + 60°) A, andi2= 10sin (400t - 60°) Athen i3=a)0b)10sin 400t Ac)-10sin 400t Ad)-5 √3 sin 400tCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Three currents i1, i2, and i3meet at a node. ifi1= 10 sin (400t + 60°) A, andi2= 10sin (400t - 60°) Athen i3=a)0b)10sin 400t Ac)-10sin 400t Ad)-5 √3 sin 400tCorrect answer is option 'C'. Can you explain this answer?.
Solutions for Three currents i1, i2, and i3meet at a node. ifi1= 10 sin (400t + 60°) A, andi2= 10sin (400t - 60°) Athen i3=a)0b)10sin 400t Ac)-10sin 400t Ad)-5 √3 sin 400tCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electrical Engineering (EE).
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
Here you can find the meaning of Three currents i1, i2, and i3meet at a node. ifi1= 10 sin (400t + 60°) A, andi2= 10sin (400t - 60°) Athen i3=a)0b)10sin 400t Ac)-10sin 400t Ad)-5 √3 sin 400tCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Three currents i1, i2, and i3meet at a node. ifi1= 10 sin (400t + 60°) A, andi2= 10sin (400t - 60°) Athen i3=a)0b)10sin 400t Ac)-10sin 400t Ad)-5 √3 sin 400tCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for Three currents i1, i2, and i3meet at a node. ifi1= 10 sin (400t + 60°) A, andi2= 10sin (400t - 60°) Athen i3=a)0b)10sin 400t Ac)-10sin 400t Ad)-5 √3 sin 400tCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of Three currents i1, i2, and i3meet at a node. ifi1= 10 sin (400t + 60°) A, andi2= 10sin (400t - 60°) Athen i3=a)0b)10sin 400t Ac)-10sin 400t Ad)-5 √3 sin 400tCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Three currents i1, i2, and i3meet at a node. ifi1= 10 sin (400t + 60°) A, andi2= 10sin (400t - 60°) Athen i3=a)0b)10sin 400t Ac)-10sin 400t Ad)-5 √3 sin 400tCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Electrical Engineering (EE) tests.
|
|
Explore Courses for Electrical Engineering (EE) exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup