Electrical Engineering (EE) Exam > Electrical Engineering (EE) Questions > How many OR gates are required for a Decimal-...
Start Learning for Free
How many OR gates are required for a Decimal-to-bcd encoder?
- a)2
- b)10
- c)3
- d)4
Correct answer is option 'D'. Can you explain this answer?
Most Upvoted Answer
How many OR gates are required for a Decimal-to-bcd encoder?a)2b)10c)3...
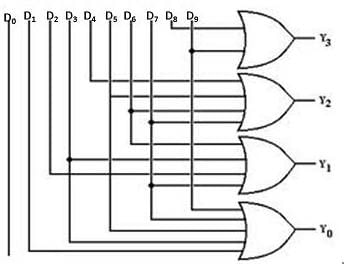
An encoder is a combinational circuit encoding the information of 2n input lines to n output lines, thus producing the binary equivalent of the input.
This is clear from the diagram that it requires 4 OR gates:
This is clear from the diagram that it requires 4 OR gates:
Free Test
FREE
| Start Free Test |
Community Answer
How many OR gates are required for a Decimal-to-bcd encoder?a)2b)10c)3...
Decimal-to-BCD Encoder
The Decimal-to-BCD (Binary-Coded Decimal) encoder is a combinational logic circuit that converts a decimal number to its BCD equivalent. BCD is a binary representation of a decimal number where each decimal digit is represented by a 4-bit binary code.
The BCD code uses four binary bits to represent each decimal digit from 0 to 9. In BCD, the binary codes for 0 to 9 are 0000 to 1001, respectively. For example, the decimal number 7 is represented in BCD as 0111.
To design a Decimal-to-BCD encoder, we need to analyze the input and output requirements.
Input: The input to the Decimal-to-BCD encoder is a 4-bit binary number representing a decimal digit. Since we are converting decimal numbers from 0 to 9, the input can have 10 possible combinations from 0000 to 1001.
Output: The output of the Decimal-to-BCD encoder is a 4-bit BCD code for the input decimal digit. Since each decimal digit is represented by a 4-bit BCD code, the output will also have 4 bits.
Logic Design: To convert a 4-bit binary number to its BCD equivalent, we need to implement a logic circuit that maps each possible input combination to its corresponding BCD output.
- We can use a truth table to determine the required logic for the Decimal-to-BCD encoder.
- The truth table will have 10 rows (for 10 input combinations from 0000 to 1001) and 4 columns (for the 4 output bits of the BCD code).
- By analyzing the truth table, we can determine the logic expressions for each output bit.
Number of OR Gates:
- The Decimal-to-BCD encoder requires 4 output bits, and each output bit can be implemented using an OR gate.
- As the correct answer is option 'D', which states that 4 OR gates are required, it aligns with the requirement of having 4 output bits in the Decimal-to-BCD encoder.
Therefore, the correct answer is option 'D' - 4.
The Decimal-to-BCD (Binary-Coded Decimal) encoder is a combinational logic circuit that converts a decimal number to its BCD equivalent. BCD is a binary representation of a decimal number where each decimal digit is represented by a 4-bit binary code.
The BCD code uses four binary bits to represent each decimal digit from 0 to 9. In BCD, the binary codes for 0 to 9 are 0000 to 1001, respectively. For example, the decimal number 7 is represented in BCD as 0111.
To design a Decimal-to-BCD encoder, we need to analyze the input and output requirements.
Input: The input to the Decimal-to-BCD encoder is a 4-bit binary number representing a decimal digit. Since we are converting decimal numbers from 0 to 9, the input can have 10 possible combinations from 0000 to 1001.
Output: The output of the Decimal-to-BCD encoder is a 4-bit BCD code for the input decimal digit. Since each decimal digit is represented by a 4-bit BCD code, the output will also have 4 bits.
Logic Design: To convert a 4-bit binary number to its BCD equivalent, we need to implement a logic circuit that maps each possible input combination to its corresponding BCD output.
- We can use a truth table to determine the required logic for the Decimal-to-BCD encoder.
- The truth table will have 10 rows (for 10 input combinations from 0000 to 1001) and 4 columns (for the 4 output bits of the BCD code).
- By analyzing the truth table, we can determine the logic expressions for each output bit.
Number of OR Gates:
- The Decimal-to-BCD encoder requires 4 output bits, and each output bit can be implemented using an OR gate.
- As the correct answer is option 'D', which states that 4 OR gates are required, it aligns with the requirement of having 4 output bits in the Decimal-to-BCD encoder.
Therefore, the correct answer is option 'D' - 4.

|
Explore Courses for Electrical Engineering (EE) exam
|

|
Question Description
How many OR gates are required for a Decimal-to-bcd encoder?a)2b)10c)3d)4Correct answer is option 'D'. Can you explain this answer? for Electrical Engineering (EE) 2025 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about How many OR gates are required for a Decimal-to-bcd encoder?a)2b)10c)3d)4Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for How many OR gates are required for a Decimal-to-bcd encoder?a)2b)10c)3d)4Correct answer is option 'D'. Can you explain this answer?.
How many OR gates are required for a Decimal-to-bcd encoder?a)2b)10c)3d)4Correct answer is option 'D'. Can you explain this answer? for Electrical Engineering (EE) 2025 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about How many OR gates are required for a Decimal-to-bcd encoder?a)2b)10c)3d)4Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for How many OR gates are required for a Decimal-to-bcd encoder?a)2b)10c)3d)4Correct answer is option 'D'. Can you explain this answer?.
Solutions for How many OR gates are required for a Decimal-to-bcd encoder?a)2b)10c)3d)4Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electrical Engineering (EE).
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
Here you can find the meaning of How many OR gates are required for a Decimal-to-bcd encoder?a)2b)10c)3d)4Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
How many OR gates are required for a Decimal-to-bcd encoder?a)2b)10c)3d)4Correct answer is option 'D'. Can you explain this answer?, a detailed solution for How many OR gates are required for a Decimal-to-bcd encoder?a)2b)10c)3d)4Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of How many OR gates are required for a Decimal-to-bcd encoder?a)2b)10c)3d)4Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice How many OR gates are required for a Decimal-to-bcd encoder?a)2b)10c)3d)4Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice Electrical Engineering (EE) tests.

|
Explore Courses for Electrical Engineering (EE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















