CAT Exam > CAT Questions > A survey was conducted among 1050 members of...
Start Learning for Free
A survey was conducted among 1050 members of a locality. There were asked about the newspaper they read among Hindu, TOI and IE. Some of the results of the survey have been tabulated as under.
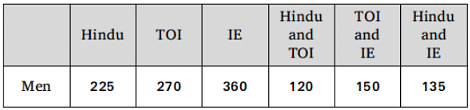
It is also known that:
I) The number of women who read only Hindu and IE is equal to the number of women who read only Hindi and TOI.
II) 20% of the people surveyed read all the three newspapers. The number of people who read exactly two newspaper is thrice the number of men who read all the three newspapers.
III) The number of women who read only Hindu is equal to the number of men who read only TOI and IE. The number of women surveyed is 150 less than the number of men surveyed.
IV) An equal number of women read TOI and IE. 495 people read Hindu and 435 people do not read IE. 10% of men read none of the newspapers.
How many women read TOI and IE both?
Correct answer is '165'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
A survey was conducted among 1050 members of a locality. There were a...
The number of women is 150 less than number of men. It means that the number of men is 600 and the number of women is 450. Also, 10% of the men do not read any newspaper i.e. 60 men do not read any newspaper. From the table we can draw the venn diagram for men as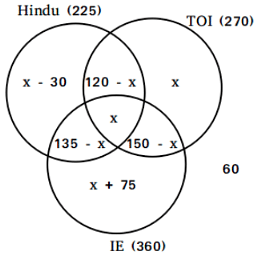
Sum of all the values must be equal to the number of men i.e. 600
Or, (x - 30) + (120 - x) + x + x + (135 - x) + (150 - x) + (x + 75) + 60 = 600
⇒ x = 90
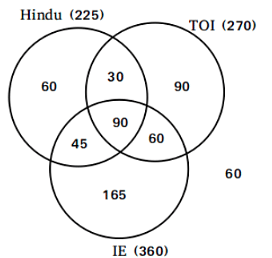
We get the venn diagram for men as:
It is given that 20% of all the people surveyed read all the three newspapers i.e. 210 people read all the three newspapers. Also, 90 men read all the three newspapers. So, 120 women must be reading all the three newspapers.
The number of women who read only Hindu is equal to the number of men who read both TOI and IE i.e. 60 women read only Hindu.
495 people read Hindu out of which 225 are men. So, 270 women must be reading Hindu.
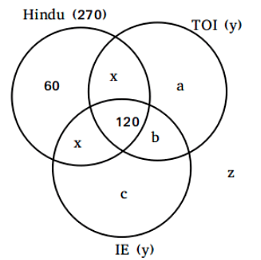
The number of women who read only Hindu and IE is equal to the number of women who read only Hindi and TOI. Let us assume it to be x.
An equal number of women read TOI and IE. Let us assume it to be y.
Also, let us assume the number of women who do not read any newspaper be z. We can draw the venn diagram for women as:
x + a + b + 120 = x + c + b + 120
⇒ a = c..........(i)
435 people do not read IE out of which 240 are men. So, 195 women do not read IE.
⇒ x + a + z + 60 = 195
⇒ x + a + z = 135............(ii)
The number of people who read exactly two newspaper is thrice the number of men who read all the three newspapers.
⇒ (30 + 45 + 60) + (x + x + b) = 3 * 90 = 270
⇒ 2x + b = 135.................(iii)
Total number of women who read Hindu = 270
Or, (60 + x + x + 120) = 270
⇒ x = 45
Putting x = 45 in (iii), we get
b = 45
Putting x = 45 in (ii), we get
a + z = 90..................(iv)
Total number of women = 450
Or, 270 + a + a + 45 + z = 450
⇒ 2a+ z = 135............(v)
On solving (iv) and (v), we get
a = 45
On putting a = 45 in (iv), we get
z = 45
Thus, we get the venn diagram for women as:
From the venn diagram for women, we can see that 165 women read TOI and IE both.
Hence, 165 is the correct answer.
Attention CAT Students!
To make sure you are not studying endlessly, EduRev has designed CAT study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in CAT.
|
Explore Courses for CAT exam
|
|
Top Courses for CATView all
A survey was conducted among 1050 members of a locality. There were asked about the newspaper they read among Hindu, TOI and IE. Some of the results of the survey have been tabulated as under.It is also known that:I) The number of women who read only Hindu and IE is equal to the number of women who read only Hindi and TOI.II) 20% of the people surveyed read all the three newspapers. The number of people who read exactly two newspaper is thrice the number of men who read all the three newspapers.III) The number of women who read only Hindu is equal to the number of men who read only TOI and IE. The number of women surveyed is 150 less than the number of men surveyed.IV) An equal number of women read TOI and IE. 495 people read Hindu and 435 people do not read IE. 10% of men read none of the newspapers.How many women read TOI and IE both?Correct answer is '165'. Can you explain this answer?
Question Description
A survey was conducted among 1050 members of a locality. There were asked about the newspaper they read among Hindu, TOI and IE. Some of the results of the survey have been tabulated as under.It is also known that:I) The number of women who read only Hindu and IE is equal to the number of women who read only Hindi and TOI.II) 20% of the people surveyed read all the three newspapers. The number of people who read exactly two newspaper is thrice the number of men who read all the three newspapers.III) The number of women who read only Hindu is equal to the number of men who read only TOI and IE. The number of women surveyed is 150 less than the number of men surveyed.IV) An equal number of women read TOI and IE. 495 people read Hindu and 435 people do not read IE. 10% of men read none of the newspapers.How many women read TOI and IE both?Correct answer is '165'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about A survey was conducted among 1050 members of a locality. There were asked about the newspaper they read among Hindu, TOI and IE. Some of the results of the survey have been tabulated as under.It is also known that:I) The number of women who read only Hindu and IE is equal to the number of women who read only Hindi and TOI.II) 20% of the people surveyed read all the three newspapers. The number of people who read exactly two newspaper is thrice the number of men who read all the three newspapers.III) The number of women who read only Hindu is equal to the number of men who read only TOI and IE. The number of women surveyed is 150 less than the number of men surveyed.IV) An equal number of women read TOI and IE. 495 people read Hindu and 435 people do not read IE. 10% of men read none of the newspapers.How many women read TOI and IE both?Correct answer is '165'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A survey was conducted among 1050 members of a locality. There were asked about the newspaper they read among Hindu, TOI and IE. Some of the results of the survey have been tabulated as under.It is also known that:I) The number of women who read only Hindu and IE is equal to the number of women who read only Hindi and TOI.II) 20% of the people surveyed read all the three newspapers. The number of people who read exactly two newspaper is thrice the number of men who read all the three newspapers.III) The number of women who read only Hindu is equal to the number of men who read only TOI and IE. The number of women surveyed is 150 less than the number of men surveyed.IV) An equal number of women read TOI and IE. 495 people read Hindu and 435 people do not read IE. 10% of men read none of the newspapers.How many women read TOI and IE both?Correct answer is '165'. Can you explain this answer?.
A survey was conducted among 1050 members of a locality. There were asked about the newspaper they read among Hindu, TOI and IE. Some of the results of the survey have been tabulated as under.It is also known that:I) The number of women who read only Hindu and IE is equal to the number of women who read only Hindi and TOI.II) 20% of the people surveyed read all the three newspapers. The number of people who read exactly two newspaper is thrice the number of men who read all the three newspapers.III) The number of women who read only Hindu is equal to the number of men who read only TOI and IE. The number of women surveyed is 150 less than the number of men surveyed.IV) An equal number of women read TOI and IE. 495 people read Hindu and 435 people do not read IE. 10% of men read none of the newspapers.How many women read TOI and IE both?Correct answer is '165'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about A survey was conducted among 1050 members of a locality. There were asked about the newspaper they read among Hindu, TOI and IE. Some of the results of the survey have been tabulated as under.It is also known that:I) The number of women who read only Hindu and IE is equal to the number of women who read only Hindi and TOI.II) 20% of the people surveyed read all the three newspapers. The number of people who read exactly two newspaper is thrice the number of men who read all the three newspapers.III) The number of women who read only Hindu is equal to the number of men who read only TOI and IE. The number of women surveyed is 150 less than the number of men surveyed.IV) An equal number of women read TOI and IE. 495 people read Hindu and 435 people do not read IE. 10% of men read none of the newspapers.How many women read TOI and IE both?Correct answer is '165'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A survey was conducted among 1050 members of a locality. There were asked about the newspaper they read among Hindu, TOI and IE. Some of the results of the survey have been tabulated as under.It is also known that:I) The number of women who read only Hindu and IE is equal to the number of women who read only Hindi and TOI.II) 20% of the people surveyed read all the three newspapers. The number of people who read exactly two newspaper is thrice the number of men who read all the three newspapers.III) The number of women who read only Hindu is equal to the number of men who read only TOI and IE. The number of women surveyed is 150 less than the number of men surveyed.IV) An equal number of women read TOI and IE. 495 people read Hindu and 435 people do not read IE. 10% of men read none of the newspapers.How many women read TOI and IE both?Correct answer is '165'. Can you explain this answer?.
Solutions for A survey was conducted among 1050 members of a locality. There were asked about the newspaper they read among Hindu, TOI and IE. Some of the results of the survey have been tabulated as under.It is also known that:I) The number of women who read only Hindu and IE is equal to the number of women who read only Hindi and TOI.II) 20% of the people surveyed read all the three newspapers. The number of people who read exactly two newspaper is thrice the number of men who read all the three newspapers.III) The number of women who read only Hindu is equal to the number of men who read only TOI and IE. The number of women surveyed is 150 less than the number of men surveyed.IV) An equal number of women read TOI and IE. 495 people read Hindu and 435 people do not read IE. 10% of men read none of the newspapers.How many women read TOI and IE both?Correct answer is '165'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT.
Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
Here you can find the meaning of A survey was conducted among 1050 members of a locality. There were asked about the newspaper they read among Hindu, TOI and IE. Some of the results of the survey have been tabulated as under.It is also known that:I) The number of women who read only Hindu and IE is equal to the number of women who read only Hindi and TOI.II) 20% of the people surveyed read all the three newspapers. The number of people who read exactly two newspaper is thrice the number of men who read all the three newspapers.III) The number of women who read only Hindu is equal to the number of men who read only TOI and IE. The number of women surveyed is 150 less than the number of men surveyed.IV) An equal number of women read TOI and IE. 495 people read Hindu and 435 people do not read IE. 10% of men read none of the newspapers.How many women read TOI and IE both?Correct answer is '165'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A survey was conducted among 1050 members of a locality. There were asked about the newspaper they read among Hindu, TOI and IE. Some of the results of the survey have been tabulated as under.It is also known that:I) The number of women who read only Hindu and IE is equal to the number of women who read only Hindi and TOI.II) 20% of the people surveyed read all the three newspapers. The number of people who read exactly two newspaper is thrice the number of men who read all the three newspapers.III) The number of women who read only Hindu is equal to the number of men who read only TOI and IE. The number of women surveyed is 150 less than the number of men surveyed.IV) An equal number of women read TOI and IE. 495 people read Hindu and 435 people do not read IE. 10% of men read none of the newspapers.How many women read TOI and IE both?Correct answer is '165'. Can you explain this answer?, a detailed solution for A survey was conducted among 1050 members of a locality. There were asked about the newspaper they read among Hindu, TOI and IE. Some of the results of the survey have been tabulated as under.It is also known that:I) The number of women who read only Hindu and IE is equal to the number of women who read only Hindi and TOI.II) 20% of the people surveyed read all the three newspapers. The number of people who read exactly two newspaper is thrice the number of men who read all the three newspapers.III) The number of women who read only Hindu is equal to the number of men who read only TOI and IE. The number of women surveyed is 150 less than the number of men surveyed.IV) An equal number of women read TOI and IE. 495 people read Hindu and 435 people do not read IE. 10% of men read none of the newspapers.How many women read TOI and IE both?Correct answer is '165'. Can you explain this answer? has been provided alongside types of A survey was conducted among 1050 members of a locality. There were asked about the newspaper they read among Hindu, TOI and IE. Some of the results of the survey have been tabulated as under.It is also known that:I) The number of women who read only Hindu and IE is equal to the number of women who read only Hindi and TOI.II) 20% of the people surveyed read all the three newspapers. The number of people who read exactly two newspaper is thrice the number of men who read all the three newspapers.III) The number of women who read only Hindu is equal to the number of men who read only TOI and IE. The number of women surveyed is 150 less than the number of men surveyed.IV) An equal number of women read TOI and IE. 495 people read Hindu and 435 people do not read IE. 10% of men read none of the newspapers.How many women read TOI and IE both?Correct answer is '165'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A survey was conducted among 1050 members of a locality. There were asked about the newspaper they read among Hindu, TOI and IE. Some of the results of the survey have been tabulated as under.It is also known that:I) The number of women who read only Hindu and IE is equal to the number of women who read only Hindi and TOI.II) 20% of the people surveyed read all the three newspapers. The number of people who read exactly two newspaper is thrice the number of men who read all the three newspapers.III) The number of women who read only Hindu is equal to the number of men who read only TOI and IE. The number of women surveyed is 150 less than the number of men surveyed.IV) An equal number of women read TOI and IE. 495 people read Hindu and 435 people do not read IE. 10% of men read none of the newspapers.How many women read TOI and IE both?Correct answer is '165'. Can you explain this answer? tests, examples and also practice CAT tests.
|
|
Explore Courses for CAT exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup