Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Questions > Which of the following data structure to conv...
Start Learning for Free
Which of the following data structure to convert an Infix expression into equivalent Prefix/Postfix notation?
- a)Array
- b)Hashing
- c)Stack
- d)Queue
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
Which of the following data structure to convert an Infix expression i...
Conversion of infix to postfix is,
Infix: ((a+b)*(c-d))
Infix: ((a+b)*(c-d))
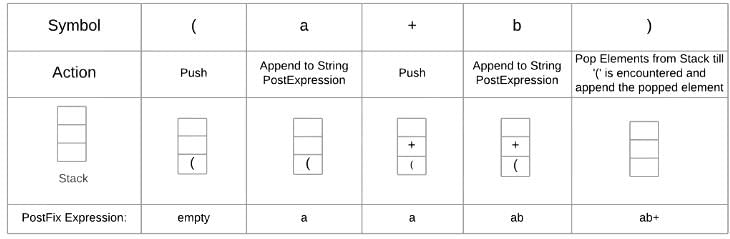
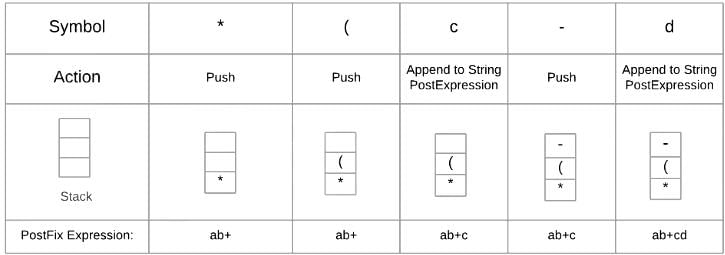
The postfix expression is ab+cd-*
Hence the correct answer is Stack.
Most Upvoted Answer
Which of the following data structure to convert an Infix expression i...
Conversion of infix to postfix is,
Infix: ((a+b)*(c-d))
Infix: ((a+b)*(c-d))
The postfix expression is ab+cd-*
Hence the correct answer is Stack.
Free Test
FREE
| Start Free Test |
Community Answer
Which of the following data structure to convert an Infix expression i...
Introduction
Converting infix expressions to prefix (Polish notation) or postfix (Reverse Polish notation) can be efficiently achieved using a stack data structure. This method is crucial in evaluating expressions without ambiguity regarding operator precedence.
Why Use a Stack?
- Last In, First Out (LIFO): Stacks operate on a LIFO principle, which is ideal for handling operators and parentheses in expressions.
- Operator Precedence: The stack allows for managing the precedence and associativity of operators effectively, ensuring that higher precedence operators are processed before lower ones.
Conversion Process
1. Infix to Postfix:
- Read the infix expression from left to right.
- If the character is an operand, add it to the output.
- If it's an operator, pop from the stack to the output until the top of the stack has an operator of less precedence, then push the current operator onto the stack.
- Handle parentheses by pushing them onto the stack and popping until a matching opening parenthesis is found.
2. Infix to Prefix:
- Reverse the infix expression.
- Swap the parentheses.
- Apply the same logic as postfix conversion using a stack to get the prefix.
Conclusion
Using a stack for these conversions allows for systematic processing of operators and operands, adhering to the rules of precedence and associativity. This method ensures that the final expression in either prefix or postfix format can be evaluated without needing to consider operator precedence again, making it efficient and straightforward.
Converting infix expressions to prefix (Polish notation) or postfix (Reverse Polish notation) can be efficiently achieved using a stack data structure. This method is crucial in evaluating expressions without ambiguity regarding operator precedence.
Why Use a Stack?
- Last In, First Out (LIFO): Stacks operate on a LIFO principle, which is ideal for handling operators and parentheses in expressions.
- Operator Precedence: The stack allows for managing the precedence and associativity of operators effectively, ensuring that higher precedence operators are processed before lower ones.
Conversion Process
1. Infix to Postfix:
- Read the infix expression from left to right.
- If the character is an operand, add it to the output.
- If it's an operator, pop from the stack to the output until the top of the stack has an operator of less precedence, then push the current operator onto the stack.
- Handle parentheses by pushing them onto the stack and popping until a matching opening parenthesis is found.
2. Infix to Prefix:
- Reverse the infix expression.
- Swap the parentheses.
- Apply the same logic as postfix conversion using a stack to get the prefix.
Conclusion
Using a stack for these conversions allows for systematic processing of operators and operands, adhering to the rules of precedence and associativity. This method ensures that the final expression in either prefix or postfix format can be evaluated without needing to consider operator precedence again, making it efficient and straightforward.
|
Explore Courses for Computer Science Engineering (CSE) exam
|
|
Similar Computer Science Engineering (CSE) Doubts
Top Courses for Computer Science Engineering (CSE)View all
Top Courses for Computer Science Engineering (CSE)
Question Description
Which of the following data structure to convert an Infix expression into equivalent Prefix/Postfix notation?a)Arrayb)Hashingc)Stackd)QueueCorrect answer is option 'C'. Can you explain this answer? for Computer Science Engineering (CSE) 2025 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Which of the following data structure to convert an Infix expression into equivalent Prefix/Postfix notation?a)Arrayb)Hashingc)Stackd)QueueCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following data structure to convert an Infix expression into equivalent Prefix/Postfix notation?a)Arrayb)Hashingc)Stackd)QueueCorrect answer is option 'C'. Can you explain this answer?.
Which of the following data structure to convert an Infix expression into equivalent Prefix/Postfix notation?a)Arrayb)Hashingc)Stackd)QueueCorrect answer is option 'C'. Can you explain this answer? for Computer Science Engineering (CSE) 2025 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Which of the following data structure to convert an Infix expression into equivalent Prefix/Postfix notation?a)Arrayb)Hashingc)Stackd)QueueCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following data structure to convert an Infix expression into equivalent Prefix/Postfix notation?a)Arrayb)Hashingc)Stackd)QueueCorrect answer is option 'C'. Can you explain this answer?.
Solutions for Which of the following data structure to convert an Infix expression into equivalent Prefix/Postfix notation?a)Arrayb)Hashingc)Stackd)QueueCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Computer Science Engineering (CSE).
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Here you can find the meaning of Which of the following data structure to convert an Infix expression into equivalent Prefix/Postfix notation?a)Arrayb)Hashingc)Stackd)QueueCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Which of the following data structure to convert an Infix expression into equivalent Prefix/Postfix notation?a)Arrayb)Hashingc)Stackd)QueueCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for Which of the following data structure to convert an Infix expression into equivalent Prefix/Postfix notation?a)Arrayb)Hashingc)Stackd)QueueCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of Which of the following data structure to convert an Infix expression into equivalent Prefix/Postfix notation?a)Arrayb)Hashingc)Stackd)QueueCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Which of the following data structure to convert an Infix expression into equivalent Prefix/Postfix notation?a)Arrayb)Hashingc)Stackd)QueueCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Computer Science Engineering (CSE) tests.
|
|
Explore Courses for Computer Science Engineering (CSE) exam
|
|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup