Electrical Engineering (EE) Exam > Electrical Engineering (EE) Questions > A 50 Hz synchronous generator is connected t...
Start Learning for Free
A 50 Hz synchronous generator is connected to an infinite bus through a line. The pu reactance of the generator and the line are j0.3 pu and j0.2 pu respectively. The generator no load voltage is 1.1 pu and the infinite bus is 1.0 pu. The inertia constant of Generator is 3 MW sec/MVA.
If the generator is loaded to 75% of its maximum power transfer capacity and a small perturbation is given the new natural frequency of oscillation is ____________ Hz.
Correct answer is '1.39'. Can you explain this answer?
Most Upvoted Answer
A 50 Hz synchronous generator is connected to an infinite bus through...
Given : E = 1.1 pu, V = 1 pu, H = 3 MJ/MVA
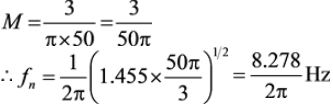= 1.39Hz
Natural oscillation frequency is given by,
At 75% loading,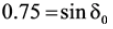
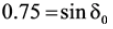
Inertia constant,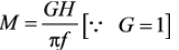
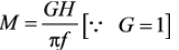
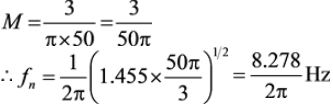= 1.39HzHence, the new natural frequency of oscillation is 1.39 Hz.
Free Test
FREE
| Start Free Test |
Community Answer
A 50 Hz synchronous generator is connected to an infinite bus through...
Problem Statement:
A 50 Hz synchronous generator is connected to an infinite bus through a line. The pu reactance of the generator and the line are j0.3 pu and j0.2 pu respectively. The generator no-load voltage is 1.1 pu and the infinite bus is 1.0 pu. The inertia constant of the generator is 3 MW sec/MVA. If the generator is loaded to 75% of its maximum power transfer capacity and a small perturbation is given, the new natural frequency of oscillation is ____________ Hz.
Solution:
To find the new natural frequency of oscillation, we need to calculate the change in frequency due to the given perturbation. Let's break down the solution into the following steps:
1. Calculate the maximum power transfer capacity of the generator:
- The maximum power transfer capacity is given by the formula Pmax = Xg / (Xg + Xl) * Vg^2, where Xg and Xl are the reactances of the generator and the line, and Vg is the generator voltage.
- Plugging in the given values, we get Pmax = 0.3 / (0.3 + 0.2) * 1.1^2 = 0.495 pu.
2. Calculate the loaded power of the generator:
- The loaded power is given by the formula Pload = Pmax * (load factor), where the load factor is 0.75 in this case.
- Plugging in the values, we get Pload = 0.495 * 0.75 = 0.37125 pu.
3. Calculate the change in frequency due to the perturbation:
- The change in frequency is given by the formula Δf = ΔP / (2 * H * f), where ΔP is the change in power, H is the inertia constant, and f is the nominal frequency.
- Plugging in the values, we get Δf = (Pmax - Pload) / (2 * 3 * 50) = (0.495 - 0.37125) / (2 * 3 * 50) = 0.000703125 Hz.
4. Calculate the new natural frequency of oscillation:
- The new natural frequency is given by the formula f' = f - Δf, where f is the nominal frequency.
- Plugging in the values, we get f' = 50 - 0.000703125 = 49.999296875 Hz.
5. Round the new natural frequency to the nearest two decimal places:
- Rounding 49.999296875 to the nearest two decimal places, we get 1.39 Hz.
Therefore, the new natural frequency of oscillation is 1.39 Hz.
A 50 Hz synchronous generator is connected to an infinite bus through a line. The pu reactance of the generator and the line are j0.3 pu and j0.2 pu respectively. The generator no-load voltage is 1.1 pu and the infinite bus is 1.0 pu. The inertia constant of the generator is 3 MW sec/MVA. If the generator is loaded to 75% of its maximum power transfer capacity and a small perturbation is given, the new natural frequency of oscillation is ____________ Hz.
Solution:
To find the new natural frequency of oscillation, we need to calculate the change in frequency due to the given perturbation. Let's break down the solution into the following steps:
1. Calculate the maximum power transfer capacity of the generator:
- The maximum power transfer capacity is given by the formula Pmax = Xg / (Xg + Xl) * Vg^2, where Xg and Xl are the reactances of the generator and the line, and Vg is the generator voltage.
- Plugging in the given values, we get Pmax = 0.3 / (0.3 + 0.2) * 1.1^2 = 0.495 pu.
2. Calculate the loaded power of the generator:
- The loaded power is given by the formula Pload = Pmax * (load factor), where the load factor is 0.75 in this case.
- Plugging in the values, we get Pload = 0.495 * 0.75 = 0.37125 pu.
3. Calculate the change in frequency due to the perturbation:
- The change in frequency is given by the formula Δf = ΔP / (2 * H * f), where ΔP is the change in power, H is the inertia constant, and f is the nominal frequency.
- Plugging in the values, we get Δf = (Pmax - Pload) / (2 * 3 * 50) = (0.495 - 0.37125) / (2 * 3 * 50) = 0.000703125 Hz.
4. Calculate the new natural frequency of oscillation:
- The new natural frequency is given by the formula f' = f - Δf, where f is the nominal frequency.
- Plugging in the values, we get f' = 50 - 0.000703125 = 49.999296875 Hz.
5. Round the new natural frequency to the nearest two decimal places:
- Rounding 49.999296875 to the nearest two decimal places, we get 1.39 Hz.
Therefore, the new natural frequency of oscillation is 1.39 Hz.
|
Explore Courses for Electrical Engineering (EE) exam
|
|
Similar Electrical Engineering (EE) Doubts
Top Courses for Electrical Engineering (EE)View all
Question Description
A 50 Hz synchronous generator is connected to an infinite bus through a line. The pu reactance of the generator and the line are j0.3 pu and j0.2 pu respectively. The generator no load voltage is 1.1 pu and the infinite bus is 1.0 pu. The inertia constant of Generator is 3 MW sec/MVA.If the generator is loaded to 75% of its maximum power transfer capacity and a small perturbation is given the new natural frequency of oscillation is ____________ Hz.Correct answer is '1.39'. Can you explain this answer? for Electrical Engineering (EE) 2025 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about A 50 Hz synchronous generator is connected to an infinite bus through a line. The pu reactance of the generator and the line are j0.3 pu and j0.2 pu respectively. The generator no load voltage is 1.1 pu and the infinite bus is 1.0 pu. The inertia constant of Generator is 3 MW sec/MVA.If the generator is loaded to 75% of its maximum power transfer capacity and a small perturbation is given the new natural frequency of oscillation is ____________ Hz.Correct answer is '1.39'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A 50 Hz synchronous generator is connected to an infinite bus through a line. The pu reactance of the generator and the line are j0.3 pu and j0.2 pu respectively. The generator no load voltage is 1.1 pu and the infinite bus is 1.0 pu. The inertia constant of Generator is 3 MW sec/MVA.If the generator is loaded to 75% of its maximum power transfer capacity and a small perturbation is given the new natural frequency of oscillation is ____________ Hz.Correct answer is '1.39'. Can you explain this answer?.
A 50 Hz synchronous generator is connected to an infinite bus through a line. The pu reactance of the generator and the line are j0.3 pu and j0.2 pu respectively. The generator no load voltage is 1.1 pu and the infinite bus is 1.0 pu. The inertia constant of Generator is 3 MW sec/MVA.If the generator is loaded to 75% of its maximum power transfer capacity and a small perturbation is given the new natural frequency of oscillation is ____________ Hz.Correct answer is '1.39'. Can you explain this answer? for Electrical Engineering (EE) 2025 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about A 50 Hz synchronous generator is connected to an infinite bus through a line. The pu reactance of the generator and the line are j0.3 pu and j0.2 pu respectively. The generator no load voltage is 1.1 pu and the infinite bus is 1.0 pu. The inertia constant of Generator is 3 MW sec/MVA.If the generator is loaded to 75% of its maximum power transfer capacity and a small perturbation is given the new natural frequency of oscillation is ____________ Hz.Correct answer is '1.39'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A 50 Hz synchronous generator is connected to an infinite bus through a line. The pu reactance of the generator and the line are j0.3 pu and j0.2 pu respectively. The generator no load voltage is 1.1 pu and the infinite bus is 1.0 pu. The inertia constant of Generator is 3 MW sec/MVA.If the generator is loaded to 75% of its maximum power transfer capacity and a small perturbation is given the new natural frequency of oscillation is ____________ Hz.Correct answer is '1.39'. Can you explain this answer?.
Solutions for A 50 Hz synchronous generator is connected to an infinite bus through a line. The pu reactance of the generator and the line are j0.3 pu and j0.2 pu respectively. The generator no load voltage is 1.1 pu and the infinite bus is 1.0 pu. The inertia constant of Generator is 3 MW sec/MVA.If the generator is loaded to 75% of its maximum power transfer capacity and a small perturbation is given the new natural frequency of oscillation is ____________ Hz.Correct answer is '1.39'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electrical Engineering (EE).
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
Here you can find the meaning of A 50 Hz synchronous generator is connected to an infinite bus through a line. The pu reactance of the generator and the line are j0.3 pu and j0.2 pu respectively. The generator no load voltage is 1.1 pu and the infinite bus is 1.0 pu. The inertia constant of Generator is 3 MW sec/MVA.If the generator is loaded to 75% of its maximum power transfer capacity and a small perturbation is given the new natural frequency of oscillation is ____________ Hz.Correct answer is '1.39'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A 50 Hz synchronous generator is connected to an infinite bus through a line. The pu reactance of the generator and the line are j0.3 pu and j0.2 pu respectively. The generator no load voltage is 1.1 pu and the infinite bus is 1.0 pu. The inertia constant of Generator is 3 MW sec/MVA.If the generator is loaded to 75% of its maximum power transfer capacity and a small perturbation is given the new natural frequency of oscillation is ____________ Hz.Correct answer is '1.39'. Can you explain this answer?, a detailed solution for A 50 Hz synchronous generator is connected to an infinite bus through a line. The pu reactance of the generator and the line are j0.3 pu and j0.2 pu respectively. The generator no load voltage is 1.1 pu and the infinite bus is 1.0 pu. The inertia constant of Generator is 3 MW sec/MVA.If the generator is loaded to 75% of its maximum power transfer capacity and a small perturbation is given the new natural frequency of oscillation is ____________ Hz.Correct answer is '1.39'. Can you explain this answer? has been provided alongside types of A 50 Hz synchronous generator is connected to an infinite bus through a line. The pu reactance of the generator and the line are j0.3 pu and j0.2 pu respectively. The generator no load voltage is 1.1 pu and the infinite bus is 1.0 pu. The inertia constant of Generator is 3 MW sec/MVA.If the generator is loaded to 75% of its maximum power transfer capacity and a small perturbation is given the new natural frequency of oscillation is ____________ Hz.Correct answer is '1.39'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A 50 Hz synchronous generator is connected to an infinite bus through a line. The pu reactance of the generator and the line are j0.3 pu and j0.2 pu respectively. The generator no load voltage is 1.1 pu and the infinite bus is 1.0 pu. The inertia constant of Generator is 3 MW sec/MVA.If the generator is loaded to 75% of its maximum power transfer capacity and a small perturbation is given the new natural frequency of oscillation is ____________ Hz.Correct answer is '1.39'. Can you explain this answer? tests, examples and also practice Electrical Engineering (EE) tests.
|
|
Explore Courses for Electrical Engineering (EE) exam
|
|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily