Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > A cold rolled steel cup, with an inside radi...
Start Learning for Free
A cold rolled steel cup, with an inside radius of 30 mm and a thickness of 3 mm, is to be drawn from a blank of diameter 40 mm. The shear yield stress and the maximum allowable stress of the material can be taken as 210 N/mm2 and 600 N/mm2, respectively.
What will be the minimum possible radius (in mm) of the cup which can be drawn from the given blank without causing a fracture?
(Answer up to one decimal place)
Correct answer is '9.2'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
A cold rolled steel cup, with an inside radius of 30 mm and a thickne...
Given data:
- Inside radius of the cup (r) = 30 mm
- Thickness of the cup (t) = 3 mm
- Diameter of the blank (D) = 40 mm
- Shear yield stress of the material (τ_yield) = 210 N/mm²
- Maximum allowable stress of the material (σ_max) = 600 N/mm²
Assumptions:
- The material is perfectly elastic and follows the maximum shear stress theory of failure.
- The cup is drawn using a single operation without any intermediate annealing or heat treatment.
- The cup is axisymmetric and there are no variations in thickness along its height.
Analysis:
The maximum shear stress (τ_max) in the cup can be given by the formula:
τ_max = 0.5 * (σ_1 - σ_3)
Where σ_1 and σ_3 are the principal stresses.
Stress Analysis:
The cup undergoes two types of stresses during the drawing process:
- Hoop stress (σ_hoop) due to radial expansion
- Longitudinal stress (σ_long) due to axial compression
Hoop Stress (σ_hoop):
The hoop stress can be calculated using the formula:
σ_hoop = P / (2 * t * r)
Where P is the drawing force.
Longitudinal Stress (σ_long):
The longitudinal stress can be calculated using the formula:
σ_long = P / (π * D * t)
Principal Stresses:
The principal stresses can be calculated using the formula:
σ_1 = (σ_hoop + σ_long) / 2 + √[((σ_hoop + σ_long) / 2)^2 + τ_max^2]
σ_3 = (σ_hoop + σ_long) / 2 - √[((σ_hoop + σ_long) / 2)^2 + τ_max^2]
Solution:
Given that the maximum allowable stress (σ_max) is 600 N/mm², we can assume that the cup will not fracture if the maximum shear stress (τ_max) is less than or equal to the shear yield stress (τ_yield).
Let's calculate the minimum possible radius (r_min) of the cup:
- Assume a value of r and calculate the values of P, σ_hoop, σ_long, σ_1, and σ_3.
- If τ_max ≤ τ_yield, increase the value of r and repeat step 1.
Free Test
FREE
| Start Free Test |
Community Answer
A cold rolled steel cup, with an inside radius of 30 mm and a thickne...
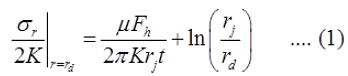
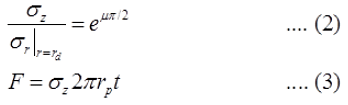
In case of σz = 600 N/mm2, from equation (2), we have
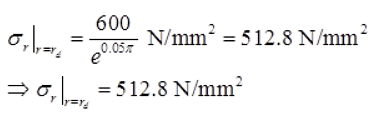
Using Equation (1) and taking Fh = 52,778 N, we get
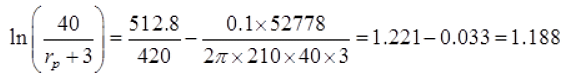
Again, it is intersecting to note that rj - rp = 30.8 mm ≥ 4t, and this goes much beyond the limit set by the plastic buckling condition.
Attention Civil Engineering (CE) Students!
To make sure you are not studying endlessly, EduRev has designed Civil Engineering (CE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Civil Engineering (CE).
|
Explore Courses for Civil Engineering (CE) exam
|
|
Similar Civil Engineering (CE) Doubts
Top Courses for Civil Engineering (CE)View all
A cold rolled steel cup, with an inside radius of 30 mm and a thickness of 3 mm, is to be drawn from a blank of diameter 40 mm. The shear yield stress and the maximum allowable stress of the material can be taken as 210 N/mm2 and 600 N/mm2, respectively.What will be the minimum possible radius (in mm) of the cup which can be drawn from the given blank without causing a fracture?(Answer up to one decimal place)Correct answer is '9.2'. Can you explain this answer?
Question Description
A cold rolled steel cup, with an inside radius of 30 mm and a thickness of 3 mm, is to be drawn from a blank of diameter 40 mm. The shear yield stress and the maximum allowable stress of the material can be taken as 210 N/mm2 and 600 N/mm2, respectively.What will be the minimum possible radius (in mm) of the cup which can be drawn from the given blank without causing a fracture?(Answer up to one decimal place)Correct answer is '9.2'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A cold rolled steel cup, with an inside radius of 30 mm and a thickness of 3 mm, is to be drawn from a blank of diameter 40 mm. The shear yield stress and the maximum allowable stress of the material can be taken as 210 N/mm2 and 600 N/mm2, respectively.What will be the minimum possible radius (in mm) of the cup which can be drawn from the given blank without causing a fracture?(Answer up to one decimal place)Correct answer is '9.2'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A cold rolled steel cup, with an inside radius of 30 mm and a thickness of 3 mm, is to be drawn from a blank of diameter 40 mm. The shear yield stress and the maximum allowable stress of the material can be taken as 210 N/mm2 and 600 N/mm2, respectively.What will be the minimum possible radius (in mm) of the cup which can be drawn from the given blank without causing a fracture?(Answer up to one decimal place)Correct answer is '9.2'. Can you explain this answer?.
A cold rolled steel cup, with an inside radius of 30 mm and a thickness of 3 mm, is to be drawn from a blank of diameter 40 mm. The shear yield stress and the maximum allowable stress of the material can be taken as 210 N/mm2 and 600 N/mm2, respectively.What will be the minimum possible radius (in mm) of the cup which can be drawn from the given blank without causing a fracture?(Answer up to one decimal place)Correct answer is '9.2'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A cold rolled steel cup, with an inside radius of 30 mm and a thickness of 3 mm, is to be drawn from a blank of diameter 40 mm. The shear yield stress and the maximum allowable stress of the material can be taken as 210 N/mm2 and 600 N/mm2, respectively.What will be the minimum possible radius (in mm) of the cup which can be drawn from the given blank without causing a fracture?(Answer up to one decimal place)Correct answer is '9.2'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A cold rolled steel cup, with an inside radius of 30 mm and a thickness of 3 mm, is to be drawn from a blank of diameter 40 mm. The shear yield stress and the maximum allowable stress of the material can be taken as 210 N/mm2 and 600 N/mm2, respectively.What will be the minimum possible radius (in mm) of the cup which can be drawn from the given blank without causing a fracture?(Answer up to one decimal place)Correct answer is '9.2'. Can you explain this answer?.
Solutions for A cold rolled steel cup, with an inside radius of 30 mm and a thickness of 3 mm, is to be drawn from a blank of diameter 40 mm. The shear yield stress and the maximum allowable stress of the material can be taken as 210 N/mm2 and 600 N/mm2, respectively.What will be the minimum possible radius (in mm) of the cup which can be drawn from the given blank without causing a fracture?(Answer up to one decimal place)Correct answer is '9.2'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of A cold rolled steel cup, with an inside radius of 30 mm and a thickness of 3 mm, is to be drawn from a blank of diameter 40 mm. The shear yield stress and the maximum allowable stress of the material can be taken as 210 N/mm2 and 600 N/mm2, respectively.What will be the minimum possible radius (in mm) of the cup which can be drawn from the given blank without causing a fracture?(Answer up to one decimal place)Correct answer is '9.2'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A cold rolled steel cup, with an inside radius of 30 mm and a thickness of 3 mm, is to be drawn from a blank of diameter 40 mm. The shear yield stress and the maximum allowable stress of the material can be taken as 210 N/mm2 and 600 N/mm2, respectively.What will be the minimum possible radius (in mm) of the cup which can be drawn from the given blank without causing a fracture?(Answer up to one decimal place)Correct answer is '9.2'. Can you explain this answer?, a detailed solution for A cold rolled steel cup, with an inside radius of 30 mm and a thickness of 3 mm, is to be drawn from a blank of diameter 40 mm. The shear yield stress and the maximum allowable stress of the material can be taken as 210 N/mm2 and 600 N/mm2, respectively.What will be the minimum possible radius (in mm) of the cup which can be drawn from the given blank without causing a fracture?(Answer up to one decimal place)Correct answer is '9.2'. Can you explain this answer? has been provided alongside types of A cold rolled steel cup, with an inside radius of 30 mm and a thickness of 3 mm, is to be drawn from a blank of diameter 40 mm. The shear yield stress and the maximum allowable stress of the material can be taken as 210 N/mm2 and 600 N/mm2, respectively.What will be the minimum possible radius (in mm) of the cup which can be drawn from the given blank without causing a fracture?(Answer up to one decimal place)Correct answer is '9.2'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A cold rolled steel cup, with an inside radius of 30 mm and a thickness of 3 mm, is to be drawn from a blank of diameter 40 mm. The shear yield stress and the maximum allowable stress of the material can be taken as 210 N/mm2 and 600 N/mm2, respectively.What will be the minimum possible radius (in mm) of the cup which can be drawn from the given blank without causing a fracture?(Answer up to one decimal place)Correct answer is '9.2'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.
|
|
Explore Courses for Civil Engineering (CE) exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup