Mechanical Engineering Exam > Mechanical Engineering Questions > A point mass is shot vertically up from groun...
Start Learning for Free
A point mass is shot vertically up from ground level with a velocity of 4 m/s at time, t = 0. It loses 20% of its impact velocity after each collision with the ground. Assuming that the acceleration due to gravity is 10 m/s2 and that air resistance is negligible, the mass stops bouncing and comes to complete rest on the ground after a total time (in seconds) of
- a)1
- b)2
- c)4
- d)∞
Correct answer is option 'C'. Can you explain this answer?
Most Upvoted Answer
A point mass is shot vertically up from ground level with a velocity o...
To solve this problem, we need to determine the time it takes for the mass to come to rest on the ground after each bounce.
After the first bounce, the mass loses 20% of its impact velocity, which is 4 m/s. Therefore, the velocity after the first bounce is 0.8 * 4 m/s = 3.2 m/s.
Using the equation v = u + at, where v is the final velocity, u is the initial velocity, a is the acceleration, and t is the time, we can solve for the time it takes for the mass to come to rest after the first bounce:
0 = 3.2 m/s + (-10 m/s^2) * t1
Solving for t1:
t1 = 3.2 m/s / 10 m/s^2 = 0.32 s
After the second bounce, the mass loses 20% of its impact velocity again. Therefore, the velocity after the second bounce is 0.8 * 3.2 m/s = 2.56 m/s.
Using the same equation as before, we can solve for the time it takes for the mass to come to rest after the second bounce:
0 = 2.56 m/s + (-10 m/s^2) * t2
Solving for t2:
t2 = 2.56 m/s / 10 m/s^2 = 0.256 s
After the third bounce, the velocity is again reduced by 20%, resulting in a velocity of 0.8 * 2.56 m/s = 2.048 m/s.
Using the same equation again, we can solve for the time it takes for the mass to come to rest after the third bounce:
0 = 2.048 m/s + (-10 m/s^2) * t3
Solving for t3:
t3 = 2.048 m/s / 10 m/s^2 = 0.2048 s
Since the mass comes to rest after the third bounce, the total time it takes for the mass to stop bouncing and come to complete rest on the ground is the sum of the times for each bounce:
Total time = t1 + t2 + t3 = 0.32 s + 0.256 s + 0.2048 s = 0.7848 s
Therefore, the answer is approximately 0.78 s.
The correct option is not provided in the given options.
After the first bounce, the mass loses 20% of its impact velocity, which is 4 m/s. Therefore, the velocity after the first bounce is 0.8 * 4 m/s = 3.2 m/s.
Using the equation v = u + at, where v is the final velocity, u is the initial velocity, a is the acceleration, and t is the time, we can solve for the time it takes for the mass to come to rest after the first bounce:
0 = 3.2 m/s + (-10 m/s^2) * t1
Solving for t1:
t1 = 3.2 m/s / 10 m/s^2 = 0.32 s
After the second bounce, the mass loses 20% of its impact velocity again. Therefore, the velocity after the second bounce is 0.8 * 3.2 m/s = 2.56 m/s.
Using the same equation as before, we can solve for the time it takes for the mass to come to rest after the second bounce:
0 = 2.56 m/s + (-10 m/s^2) * t2
Solving for t2:
t2 = 2.56 m/s / 10 m/s^2 = 0.256 s
After the third bounce, the velocity is again reduced by 20%, resulting in a velocity of 0.8 * 2.56 m/s = 2.048 m/s.
Using the same equation again, we can solve for the time it takes for the mass to come to rest after the third bounce:
0 = 2.048 m/s + (-10 m/s^2) * t3
Solving for t3:
t3 = 2.048 m/s / 10 m/s^2 = 0.2048 s
Since the mass comes to rest after the third bounce, the total time it takes for the mass to stop bouncing and come to complete rest on the ground is the sum of the times for each bounce:
Total time = t1 + t2 + t3 = 0.32 s + 0.256 s + 0.2048 s = 0.7848 s
Therefore, the answer is approximately 0.78 s.
The correct option is not provided in the given options.
Free Test
FREE
| Start Free Test |
Community Answer
A point mass is shot vertically up from ground level with a velocity o...
Under the given situation the ball will go up reach to a maximum height then come down, with the same initial velocity it will hit the ground but when it bounced back it will loss 20% of the velocity hence will move up with an initial velocity of 80% of the previous initial velocity. Thus, the time of flight will keep on decreasing with the collisions. The situation will look like this.
Let (vi) be the initial velocity, after (ith) collision
From the data we know (Loss of velocity 20%)
(u1 = 4 m/s) * and [u(i+1) = 0.08 Ui]
Now the time of flight in each collision: [time to go up = time to come down]
v = u + at
Where, a ⇒ (g) = -10 m/s2 ↑ (- ve acceleration)
u = Initial velocity; v = final velocity
At the top (v = 0); t = time taken
0 = u – gt ⇒ t = (u/g)
Now, total time of flight = (2 times) the time to go up.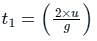
So, in (ith) collision the time of flight is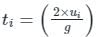
Total time will be summation of all the time of flight
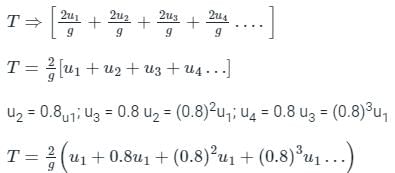
Now, this looks like a geometric progression (G.P) with ratio of (0.8)
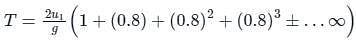
Now to final the sum of the G.P, [1 + 0.8 + (0.8)2 + (0.8)3 + ….]
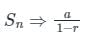
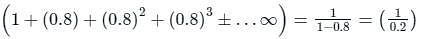
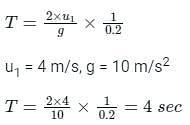
Mistakes
Here, the mistake that can happen is one can confuse 20% loss as (20% of the velocity). So, instead (0.8 u) You will take (0.2 u) as the velocity after the collision which will result in following.
Which is not correct
Another mistake is the time of flight calculation
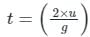instead you might commit a mistake of taking (u/g) as the time of flight in hurry as you forget to take the time of ball to come down which is same as time to go up.
Which will result in (1/2) of the answer
⇒ (1/2) x 4 = 2 sec which is not correct.
Let (vi) be the initial velocity, after (ith) collision
From the data we know (Loss of velocity 20%)
(u1 = 4 m/s) * and [u(i+1) = 0.08 Ui]
Now the time of flight in each collision: [time to go up = time to come down]
v = u + at
Where, a ⇒ (g) = -10 m/s2 ↑ (- ve acceleration)
u = Initial velocity; v = final velocity
At the top (v = 0); t = time taken
0 = u – gt ⇒ t = (u/g)
Now, total time of flight = (2 times) the time to go up.
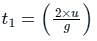
So, in (ith) collision the time of flight is
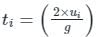
Total time will be summation of all the time of flight
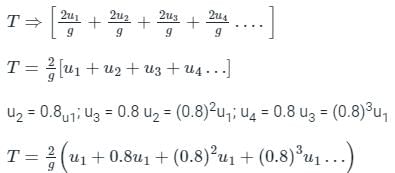
Now, this looks like a geometric progression (G.P) with ratio of (0.8)
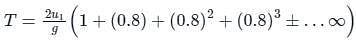
Now to final the sum of the G.P, [1 + 0.8 + (0.8)2 + (0.8)3 + ….]
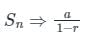
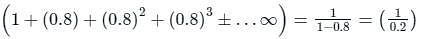
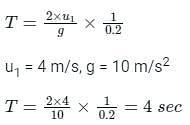
Mistakes
Here, the mistake that can happen is one can confuse 20% loss as (20% of the velocity). So, instead (0.8 u) You will take (0.2 u) as the velocity after the collision which will result in following.
Which is not correct
Another mistake is the time of flight calculation
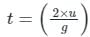instead you might commit a mistake of taking (u/g) as the time of flight in hurry as you forget to take the time of ball to come down which is same as time to go up.Which will result in (1/2) of the answer
⇒ (1/2) x 4 = 2 sec which is not correct.
|
Explore Courses for Mechanical Engineering exam
|
|
Similar Mechanical Engineering Doubts
Top Courses for Mechanical EngineeringView all
A point mass is shot vertically up from ground level with a velocity of 4 m/s at time, t = 0. It loses 20% of its impact velocity after each collision with the ground. Assuming that the acceleration due to gravity is 10 m/s2 and that air resistance is negligible, the mass stops bouncing and comes to complete rest on the ground after a total time (in seconds) ofa)1b)2c)4d)∞Correct answer is option 'C'. Can you explain this answer?
Question Description
A point mass is shot vertically up from ground level with a velocity of 4 m/s at time, t = 0. It loses 20% of its impact velocity after each collision with the ground. Assuming that the acceleration due to gravity is 10 m/s2 and that air resistance is negligible, the mass stops bouncing and comes to complete rest on the ground after a total time (in seconds) ofa)1b)2c)4d)∞Correct answer is option 'C'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about A point mass is shot vertically up from ground level with a velocity of 4 m/s at time, t = 0. It loses 20% of its impact velocity after each collision with the ground. Assuming that the acceleration due to gravity is 10 m/s2 and that air resistance is negligible, the mass stops bouncing and comes to complete rest on the ground after a total time (in seconds) ofa)1b)2c)4d)∞Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A point mass is shot vertically up from ground level with a velocity of 4 m/s at time, t = 0. It loses 20% of its impact velocity after each collision with the ground. Assuming that the acceleration due to gravity is 10 m/s2 and that air resistance is negligible, the mass stops bouncing and comes to complete rest on the ground after a total time (in seconds) ofa)1b)2c)4d)∞Correct answer is option 'C'. Can you explain this answer?.
A point mass is shot vertically up from ground level with a velocity of 4 m/s at time, t = 0. It loses 20% of its impact velocity after each collision with the ground. Assuming that the acceleration due to gravity is 10 m/s2 and that air resistance is negligible, the mass stops bouncing and comes to complete rest on the ground after a total time (in seconds) ofa)1b)2c)4d)∞Correct answer is option 'C'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about A point mass is shot vertically up from ground level with a velocity of 4 m/s at time, t = 0. It loses 20% of its impact velocity after each collision with the ground. Assuming that the acceleration due to gravity is 10 m/s2 and that air resistance is negligible, the mass stops bouncing and comes to complete rest on the ground after a total time (in seconds) ofa)1b)2c)4d)∞Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A point mass is shot vertically up from ground level with a velocity of 4 m/s at time, t = 0. It loses 20% of its impact velocity after each collision with the ground. Assuming that the acceleration due to gravity is 10 m/s2 and that air resistance is negligible, the mass stops bouncing and comes to complete rest on the ground after a total time (in seconds) ofa)1b)2c)4d)∞Correct answer is option 'C'. Can you explain this answer?.
Solutions for A point mass is shot vertically up from ground level with a velocity of 4 m/s at time, t = 0. It loses 20% of its impact velocity after each collision with the ground. Assuming that the acceleration due to gravity is 10 m/s2 and that air resistance is negligible, the mass stops bouncing and comes to complete rest on the ground after a total time (in seconds) ofa)1b)2c)4d)∞Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of A point mass is shot vertically up from ground level with a velocity of 4 m/s at time, t = 0. It loses 20% of its impact velocity after each collision with the ground. Assuming that the acceleration due to gravity is 10 m/s2 and that air resistance is negligible, the mass stops bouncing and comes to complete rest on the ground after a total time (in seconds) ofa)1b)2c)4d)∞Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A point mass is shot vertically up from ground level with a velocity of 4 m/s at time, t = 0. It loses 20% of its impact velocity after each collision with the ground. Assuming that the acceleration due to gravity is 10 m/s2 and that air resistance is negligible, the mass stops bouncing and comes to complete rest on the ground after a total time (in seconds) ofa)1b)2c)4d)∞Correct answer is option 'C'. Can you explain this answer?, a detailed solution for A point mass is shot vertically up from ground level with a velocity of 4 m/s at time, t = 0. It loses 20% of its impact velocity after each collision with the ground. Assuming that the acceleration due to gravity is 10 m/s2 and that air resistance is negligible, the mass stops bouncing and comes to complete rest on the ground after a total time (in seconds) ofa)1b)2c)4d)∞Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of A point mass is shot vertically up from ground level with a velocity of 4 m/s at time, t = 0. It loses 20% of its impact velocity after each collision with the ground. Assuming that the acceleration due to gravity is 10 m/s2 and that air resistance is negligible, the mass stops bouncing and comes to complete rest on the ground after a total time (in seconds) ofa)1b)2c)4d)∞Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A point mass is shot vertically up from ground level with a velocity of 4 m/s at time, t = 0. It loses 20% of its impact velocity after each collision with the ground. Assuming that the acceleration due to gravity is 10 m/s2 and that air resistance is negligible, the mass stops bouncing and comes to complete rest on the ground after a total time (in seconds) ofa)1b)2c)4d)∞Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.
|
|
Explore Courses for Mechanical Engineering exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup