CAT Exam > CAT Questions > In a triangle ABC, with AB=24 cm, BC= 36 cm a...
Start Learning for Free
In a triangle ABC, with AB=24 cm, BC= 36 cm and AC= 50 cm, a semicircle is drawn inside the triangle such that its diameter lies on AC and is tangent to AB and BC. If O is the centre of the semi-circle, find the measure of line AO.
- a)25 cm
- b)18 cm
- c)15 cm
- d)20 cm
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
In a triangle ABC, with AB=24 cm, BC= 36 cm and AC= 50 cm, a semicircl...
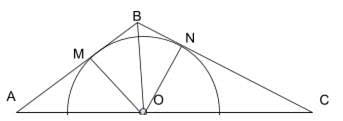
MB= BN ( B is an external point and BM and Bn are tangents to the circle).
Angles BMO and BNO= 90 degrees and OB is common to both. Hence, triangles OBM and OBN are congruent triangles.
So, OB bisects angle B and hence;
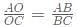
⇒
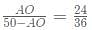
⇒ 3AO=2(50−AO)
⇒ 5AO = 100.
.'. AO= 20 cm
Free Test
FREE
| Start Free Test |
Community Answer
In a triangle ABC, with AB=24 cm, BC= 36 cm and AC= 50 cm, a semicircl...
To find the measure of line AO, we can use the properties of a triangle inscribed in a semicircle.
1. Draw the diagram:
Let's start by drawing the triangle ABC with the given measurements.
AB = 24 cm, BC = 36 cm, and AC = 50 cm.
Draw a semicircle inside the triangle, with its diameter lying on AC and tangent to AB and BC. Label the center of the semicircle as O.
2. Identify the key points:
We need to find the measure of line AO.
3. Use the properties of a triangle inscribed in a semicircle:
In a triangle inscribed in a semicircle, the diameter of the semicircle is perpendicular to the base of the triangle. Therefore, angle AOC is a right angle.
4. Apply the Pythagorean theorem:
Since angle AOC is a right angle, we can use the Pythagorean theorem to find the measure of AO.
In right triangle AOC, AO^2 + OC^2 = AC^2.
5. Find the length of OC:
To find the length of OC, we need to use the property that a radius of a circle is perpendicular to the tangent line at the point of tangency.
Since OC is the radius of the semicircle and is perpendicular to AB, we can conclude that triangle OCA is a right triangle.
Using the Pythagorean theorem in right triangle OCA, we have:
OC^2 + AC^2 = OA^2.
6. Substitute the values:
Substituting the given measurements, we have:
OC^2 + 50^2 = OA^2. ...(1)
OC^2 + 24^2 = 36^2. ...(2)
7. Solve the equations:
Subtracting equation (2) from equation (1), we get:
OA^2 - 36^2 = 50^2 - 24^2.
Simplifying, we have:
OA^2 - 1296 = 2500 - 576.
OA^2 - 1296 = 1924.
OA^2 = 1296 + 1924.
OA^2 = 3220.
Taking the square root of both sides, we have:
OA = √3220.
OA ≈ 56.77 cm.
8. Determine the correct answer:
The measure of line AO is approximately 56.77 cm, which is closest to 20 cm. Therefore, the correct answer is option D) 20 cm.
1. Draw the diagram:
Let's start by drawing the triangle ABC with the given measurements.
AB = 24 cm, BC = 36 cm, and AC = 50 cm.
Draw a semicircle inside the triangle, with its diameter lying on AC and tangent to AB and BC. Label the center of the semicircle as O.
2. Identify the key points:
We need to find the measure of line AO.
3. Use the properties of a triangle inscribed in a semicircle:
In a triangle inscribed in a semicircle, the diameter of the semicircle is perpendicular to the base of the triangle. Therefore, angle AOC is a right angle.
4. Apply the Pythagorean theorem:
Since angle AOC is a right angle, we can use the Pythagorean theorem to find the measure of AO.
In right triangle AOC, AO^2 + OC^2 = AC^2.
5. Find the length of OC:
To find the length of OC, we need to use the property that a radius of a circle is perpendicular to the tangent line at the point of tangency.
Since OC is the radius of the semicircle and is perpendicular to AB, we can conclude that triangle OCA is a right triangle.
Using the Pythagorean theorem in right triangle OCA, we have:
OC^2 + AC^2 = OA^2.
6. Substitute the values:
Substituting the given measurements, we have:
OC^2 + 50^2 = OA^2. ...(1)
OC^2 + 24^2 = 36^2. ...(2)
7. Solve the equations:
Subtracting equation (2) from equation (1), we get:
OA^2 - 36^2 = 50^2 - 24^2.
Simplifying, we have:
OA^2 - 1296 = 2500 - 576.
OA^2 - 1296 = 1924.
OA^2 = 1296 + 1924.
OA^2 = 3220.
Taking the square root of both sides, we have:
OA = √3220.
OA ≈ 56.77 cm.
8. Determine the correct answer:
The measure of line AO is approximately 56.77 cm, which is closest to 20 cm. Therefore, the correct answer is option D) 20 cm.
Attention CAT Students!
To make sure you are not studying endlessly, EduRev has designed CAT study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in CAT.

|
Explore Courses for CAT exam
|

|
Similar CAT Doubts
In a triangle ABC, with AB=24 cm, BC= 36 cm and AC= 50 cm, a semicircle is drawn inside the triangle such that its diameter lies on AC and is tangent to AB and BC. If O is the centre of the semi-circle, find the measure of line AO.a)25 cmb)18 cmc)15 cmd)20 cmCorrect answer is option 'D'. Can you explain this answer?
Question Description
In a triangle ABC, with AB=24 cm, BC= 36 cm and AC= 50 cm, a semicircle is drawn inside the triangle such that its diameter lies on AC and is tangent to AB and BC. If O is the centre of the semi-circle, find the measure of line AO.a)25 cmb)18 cmc)15 cmd)20 cmCorrect answer is option 'D'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about In a triangle ABC, with AB=24 cm, BC= 36 cm and AC= 50 cm, a semicircle is drawn inside the triangle such that its diameter lies on AC and is tangent to AB and BC. If O is the centre of the semi-circle, find the measure of line AO.a)25 cmb)18 cmc)15 cmd)20 cmCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In a triangle ABC, with AB=24 cm, BC= 36 cm and AC= 50 cm, a semicircle is drawn inside the triangle such that its diameter lies on AC and is tangent to AB and BC. If O is the centre of the semi-circle, find the measure of line AO.a)25 cmb)18 cmc)15 cmd)20 cmCorrect answer is option 'D'. Can you explain this answer?.
In a triangle ABC, with AB=24 cm, BC= 36 cm and AC= 50 cm, a semicircle is drawn inside the triangle such that its diameter lies on AC and is tangent to AB and BC. If O is the centre of the semi-circle, find the measure of line AO.a)25 cmb)18 cmc)15 cmd)20 cmCorrect answer is option 'D'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about In a triangle ABC, with AB=24 cm, BC= 36 cm and AC= 50 cm, a semicircle is drawn inside the triangle such that its diameter lies on AC and is tangent to AB and BC. If O is the centre of the semi-circle, find the measure of line AO.a)25 cmb)18 cmc)15 cmd)20 cmCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In a triangle ABC, with AB=24 cm, BC= 36 cm and AC= 50 cm, a semicircle is drawn inside the triangle such that its diameter lies on AC and is tangent to AB and BC. If O is the centre of the semi-circle, find the measure of line AO.a)25 cmb)18 cmc)15 cmd)20 cmCorrect answer is option 'D'. Can you explain this answer?.
Solutions for In a triangle ABC, with AB=24 cm, BC= 36 cm and AC= 50 cm, a semicircle is drawn inside the triangle such that its diameter lies on AC and is tangent to AB and BC. If O is the centre of the semi-circle, find the measure of line AO.a)25 cmb)18 cmc)15 cmd)20 cmCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT.
Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
Here you can find the meaning of In a triangle ABC, with AB=24 cm, BC= 36 cm and AC= 50 cm, a semicircle is drawn inside the triangle such that its diameter lies on AC and is tangent to AB and BC. If O is the centre of the semi-circle, find the measure of line AO.a)25 cmb)18 cmc)15 cmd)20 cmCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
In a triangle ABC, with AB=24 cm, BC= 36 cm and AC= 50 cm, a semicircle is drawn inside the triangle such that its diameter lies on AC and is tangent to AB and BC. If O is the centre of the semi-circle, find the measure of line AO.a)25 cmb)18 cmc)15 cmd)20 cmCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for In a triangle ABC, with AB=24 cm, BC= 36 cm and AC= 50 cm, a semicircle is drawn inside the triangle such that its diameter lies on AC and is tangent to AB and BC. If O is the centre of the semi-circle, find the measure of line AO.a)25 cmb)18 cmc)15 cmd)20 cmCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of In a triangle ABC, with AB=24 cm, BC= 36 cm and AC= 50 cm, a semicircle is drawn inside the triangle such that its diameter lies on AC and is tangent to AB and BC. If O is the centre of the semi-circle, find the measure of line AO.a)25 cmb)18 cmc)15 cmd)20 cmCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice In a triangle ABC, with AB=24 cm, BC= 36 cm and AC= 50 cm, a semicircle is drawn inside the triangle such that its diameter lies on AC and is tangent to AB and BC. If O is the centre of the semi-circle, find the measure of line AO.a)25 cmb)18 cmc)15 cmd)20 cmCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice CAT tests.

|
Explore Courses for CAT exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























