Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > St. venant equations representa)continuity eq...
Start Learning for Free
St. venant equations represent
- a)continuity equation in two different forms
- b)continuity and momentum equation
- c)momentum and energy equation
- d)momentum equation in two different forms
Correct answer is option 'B'. Can you explain this answer?
Most Upvoted Answer
St. venant equations representa)continuity equation in two different f...
Continuity and Momentum Equation
a) Continuity Equation in two different forms:
The continuity equation is a fundamental principle in fluid dynamics that states that the mass of fluid entering a control volume must be equal to the mass of fluid leaving the control volume, assuming no sources or sinks of fluid exist within the control volume. The continuity equation can be expressed in two different forms:
1. Differential form:
The differential form of the continuity equation represents the rate of change of mass within an infinitesimally small control volume. It is given by:
∂ρ/∂t + ∇·(ρv) = 0
where:
- ∂ρ/∂t is the rate of change of density with respect to time
- ∇·(ρv) is the divergence of the mass flux density vector (ρv), which represents the rate of mass flow per unit volume
2. Integral form:
The integral form of the continuity equation represents the overall mass balance over a finite control volume. It is given by:
∫(∂ρ/∂t)dV + ∮(ρv·dA) = 0
where:
- ∫(∂ρ/∂t)dV is the integral of the rate of change of density with respect to time over the control volume
- ∮(ρv·dA) is the integral of the mass flux density vector (ρv) dotted with the outward unit normal vector (dA) over the control surface
b) Continuity and Momentum Equation:
The continuity equation is closely related to the momentum equation, as both are derived from the principles of conservation of mass and momentum. The continuity equation ensures that mass is conserved within a control volume, while the momentum equation ensures that momentum is conserved.
The momentum equation can be expressed in terms of the Navier-Stokes equations, which are a set of partial differential equations that describe the motion of fluid:
ρ(∂v/∂t + v·∇v) = -∇p + μ∇^2v + ρg
where:
- ρ is the density of the fluid
- v is the velocity vector
- ∂v/∂t is the rate of change of velocity with respect to time
- ∇v is the gradient of the velocity vector
- p is the pressure
- μ is the dynamic viscosity of the fluid
- ∇^2v is the Laplacian of the velocity vector
- g is the acceleration due to gravity
The continuity equation is incorporated into the momentum equation through the divergence term (∇·v), which represents the rate of change of velocity with respect to position. This ensures that the change in mass within the control volume is accounted for in the momentum equation.
Summary:
The correct answer is option 'B' because the continuity equation and the momentum equation are closely related and are both essential in describing the behavior of fluid flow. The continuity equation ensures mass conservation, while the momentum equation ensures momentum conservation.
a) Continuity Equation in two different forms:
The continuity equation is a fundamental principle in fluid dynamics that states that the mass of fluid entering a control volume must be equal to the mass of fluid leaving the control volume, assuming no sources or sinks of fluid exist within the control volume. The continuity equation can be expressed in two different forms:
1. Differential form:
The differential form of the continuity equation represents the rate of change of mass within an infinitesimally small control volume. It is given by:
∂ρ/∂t + ∇·(ρv) = 0
where:
- ∂ρ/∂t is the rate of change of density with respect to time
- ∇·(ρv) is the divergence of the mass flux density vector (ρv), which represents the rate of mass flow per unit volume
2. Integral form:
The integral form of the continuity equation represents the overall mass balance over a finite control volume. It is given by:
∫(∂ρ/∂t)dV + ∮(ρv·dA) = 0
where:
- ∫(∂ρ/∂t)dV is the integral of the rate of change of density with respect to time over the control volume
- ∮(ρv·dA) is the integral of the mass flux density vector (ρv) dotted with the outward unit normal vector (dA) over the control surface
b) Continuity and Momentum Equation:
The continuity equation is closely related to the momentum equation, as both are derived from the principles of conservation of mass and momentum. The continuity equation ensures that mass is conserved within a control volume, while the momentum equation ensures that momentum is conserved.
The momentum equation can be expressed in terms of the Navier-Stokes equations, which are a set of partial differential equations that describe the motion of fluid:
ρ(∂v/∂t + v·∇v) = -∇p + μ∇^2v + ρg
where:
- ρ is the density of the fluid
- v is the velocity vector
- ∂v/∂t is the rate of change of velocity with respect to time
- ∇v is the gradient of the velocity vector
- p is the pressure
- μ is the dynamic viscosity of the fluid
- ∇^2v is the Laplacian of the velocity vector
- g is the acceleration due to gravity
The continuity equation is incorporated into the momentum equation through the divergence term (∇·v), which represents the rate of change of velocity with respect to position. This ensures that the change in mass within the control volume is accounted for in the momentum equation.
Summary:
The correct answer is option 'B' because the continuity equation and the momentum equation are closely related and are both essential in describing the behavior of fluid flow. The continuity equation ensures mass conservation, while the momentum equation ensures momentum conservation.
Free Test
FREE
| Start Free Test |
Community Answer
St. venant equations representa)continuity equation in two different f...
St. Venant Equations:
1. Continuity equation
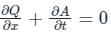
2. Momentum Equation
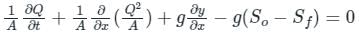
Assumptions for St. Venant Equations
1. Continuity equation
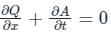
2. Momentum Equation
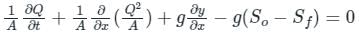
Assumptions for St. Venant Equations
- Flow is one-dimensional
- Hydrostatic pressure prevails and vertical accelerations are negligible
- Streamline curvature is small.
- Bottom slope of the channel is small.
- Manning’s equation is used to describe resistance effects
- The fluid is incompressible
Hence, St. venant equations represent continuity and momentum equations.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Question Description
St. venant equations representa)continuity equation in two different formsb)continuity and momentum equationc)momentum and energy equationd)momentum equation in two different formsCorrect answer is option 'B'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about St. venant equations representa)continuity equation in two different formsb)continuity and momentum equationc)momentum and energy equationd)momentum equation in two different formsCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for St. venant equations representa)continuity equation in two different formsb)continuity and momentum equationc)momentum and energy equationd)momentum equation in two different formsCorrect answer is option 'B'. Can you explain this answer?.
St. venant equations representa)continuity equation in two different formsb)continuity and momentum equationc)momentum and energy equationd)momentum equation in two different formsCorrect answer is option 'B'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about St. venant equations representa)continuity equation in two different formsb)continuity and momentum equationc)momentum and energy equationd)momentum equation in two different formsCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for St. venant equations representa)continuity equation in two different formsb)continuity and momentum equationc)momentum and energy equationd)momentum equation in two different formsCorrect answer is option 'B'. Can you explain this answer?.
Solutions for St. venant equations representa)continuity equation in two different formsb)continuity and momentum equationc)momentum and energy equationd)momentum equation in two different formsCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of St. venant equations representa)continuity equation in two different formsb)continuity and momentum equationc)momentum and energy equationd)momentum equation in two different formsCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
St. venant equations representa)continuity equation in two different formsb)continuity and momentum equationc)momentum and energy equationd)momentum equation in two different formsCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for St. venant equations representa)continuity equation in two different formsb)continuity and momentum equationc)momentum and energy equationd)momentum equation in two different formsCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of St. venant equations representa)continuity equation in two different formsb)continuity and momentum equationc)momentum and energy equationd)momentum equation in two different formsCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice St. venant equations representa)continuity equation in two different formsb)continuity and momentum equationc)momentum and energy equationd)momentum equation in two different formsCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























