CAT Exam > CAT Questions > An express train travelling at a speed of 72 ...
Start Learning for Free
An express train travelling at a speed of 72 km/hr crosses a goods train travelling at a speed of 45 km/hr in the opposite direction in half a minute. If the express train were to overtake the goods train while moving in the same direction, then how long would it take to do so? (Assume that the trains continue to travel at the same respective speeds as mentioned earlier.)
- a)170 seconds
- b)130 seconds
- c)150 seconds
- d)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
An express train travelling at a speed of 72 km/hr crosses a goods tra...
When two trains cross each other while moving in the opposite direction or when a train overtakes another train, the distance covered by the express train is equal to the sum of the lengths of both the trains.
Case 1: When the trains travel in opposite directions:
Distance travelled = Sum of lengths of the two trains = Relative speeds of the trains × Time taken
In this case, relative speeds = 72 + 45 = 117 km/hr (Relative speed when two objects travel in opposite directions = Sum of the individual speeds)
Time taken = Half a minute = 30 seconds
As the speed is in km/hr and time is in seconds, let us convert the speed into m/sec to ensure congruency in the units.
117 km/hr =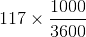
= 
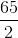m/sec
Therefore, distance covered = Sum of the lengths of the two trains =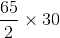
= 975 metres
Case 2: When the trains are travelling in the same direction:
Distance travelled = Sum of the lengths of the two trains = Relative speed × Time taken
Relative speed = (72 - 45) = 27 km/hr (When two objects travel in the same direction, their relative speed is equal to the difference between their individual speeds.)
As the lengths of the two trains will remain the same, irrespective of their direction of travel, the distance travelled will be the same in both the cases = 975 m
Converting 27 km/hr into m/sec, we get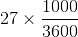
= 
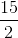m/sec
975 m =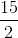
× Time taken (in seconds)
Time taken =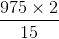
= 130 seconds
Case 1: When the trains travel in opposite directions:
Distance travelled = Sum of lengths of the two trains = Relative speeds of the trains × Time taken
In this case, relative speeds = 72 + 45 = 117 km/hr (Relative speed when two objects travel in opposite directions = Sum of the individual speeds)
Time taken = Half a minute = 30 seconds
As the speed is in km/hr and time is in seconds, let us convert the speed into m/sec to ensure congruency in the units.
117 km/hr =
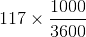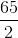= m/secTherefore, distance covered = Sum of the lengths of the two trains =
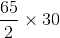= 975 metresCase 2: When the trains are travelling in the same direction:
Distance travelled = Sum of the lengths of the two trains = Relative speed × Time taken
Relative speed = (72 - 45) = 27 km/hr (When two objects travel in the same direction, their relative speed is equal to the difference between their individual speeds.)
As the lengths of the two trains will remain the same, irrespective of their direction of travel, the distance travelled will be the same in both the cases = 975 m
Converting 27 km/hr into m/sec, we get
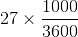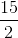= m/sec 975 m =
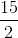× Time taken (in seconds) Time taken =
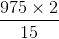= 130 secondsFree Test
FREE
| Start Free Test |
Community Answer
An express train travelling at a speed of 72 km/hr crosses a goods tra...
Let's assume the length of the express train is 'a' km and the length of the goods train is 'b' km.
Given:
Speed of the express train = 72 km/hr
Speed of the goods train = 45 km/hr
Time taken to cross the goods train in opposite direction = 0.5 minutes
To find:
Time taken by the express train to overtake the goods train in the same direction.
We know that:
Distance = Speed * Time
1. Crossing the goods train in opposite direction:
Distance covered by the express train = Length of the express train (a) + Length of the goods train (b)
Relative speed = Speed of the express train + Speed of the goods train = 72 + 45 = 117 km/hr
Distance covered = Relative speed * Time
(a + b) = 117 * (0.5/60) [Converting time from minutes to hours]
(a + b) = 117/120 km
2. Overtaking the goods train in the same direction:
Relative speed = Speed of the express train - Speed of the goods train = 72 - 45 = 27 km/hr
We need to find the time taken (t) by the express train to cover the distance (a + b) at a relative speed of 27 km/hr.
Distance covered = Relative speed * Time
(a + b) = 27 * (t/60) [Converting time from minutes to hours]
(a + b) = 27/60 * t
t = (a + b) * 60/27
Substituting the value of (a + b) from the previous equation:
t = (117/120) * 60/27
t = 130 seconds
Hence, the express train would take 130 seconds to overtake the goods train while moving in the same direction.
Therefore, option B is the correct answer.
Given:
Speed of the express train = 72 km/hr
Speed of the goods train = 45 km/hr
Time taken to cross the goods train in opposite direction = 0.5 minutes
To find:
Time taken by the express train to overtake the goods train in the same direction.
We know that:
Distance = Speed * Time
1. Crossing the goods train in opposite direction:
Distance covered by the express train = Length of the express train (a) + Length of the goods train (b)
Relative speed = Speed of the express train + Speed of the goods train = 72 + 45 = 117 km/hr
Distance covered = Relative speed * Time
(a + b) = 117 * (0.5/60) [Converting time from minutes to hours]
(a + b) = 117/120 km
2. Overtaking the goods train in the same direction:
Relative speed = Speed of the express train - Speed of the goods train = 72 - 45 = 27 km/hr
We need to find the time taken (t) by the express train to cover the distance (a + b) at a relative speed of 27 km/hr.
Distance covered = Relative speed * Time
(a + b) = 27 * (t/60) [Converting time from minutes to hours]
(a + b) = 27/60 * t
t = (a + b) * 60/27
Substituting the value of (a + b) from the previous equation:
t = (117/120) * 60/27
t = 130 seconds
Hence, the express train would take 130 seconds to overtake the goods train while moving in the same direction.
Therefore, option B is the correct answer.
Attention CAT Students!
To make sure you are not studying endlessly, EduRev has designed CAT study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in CAT.
|
Explore Courses for CAT exam
|
|
Top Courses for CATView all
An express train travelling at a speed of 72 km/hr crosses a goods train travelling at a speed of 45 km/hr in the opposite direction in half a minute. If the express train were to overtake the goods train while moving in the same direction, then how long would it take to do so? (Assume that the trains continue to travel at the same respective speeds as mentioned earlier.)a)170 secondsb)130 secondsc)150 secondsd)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer?
Question Description
An express train travelling at a speed of 72 km/hr crosses a goods train travelling at a speed of 45 km/hr in the opposite direction in half a minute. If the express train were to overtake the goods train while moving in the same direction, then how long would it take to do so? (Assume that the trains continue to travel at the same respective speeds as mentioned earlier.)a)170 secondsb)130 secondsc)150 secondsd)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about An express train travelling at a speed of 72 km/hr crosses a goods train travelling at a speed of 45 km/hr in the opposite direction in half a minute. If the express train were to overtake the goods train while moving in the same direction, then how long would it take to do so? (Assume that the trains continue to travel at the same respective speeds as mentioned earlier.)a)170 secondsb)130 secondsc)150 secondsd)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An express train travelling at a speed of 72 km/hr crosses a goods train travelling at a speed of 45 km/hr in the opposite direction in half a minute. If the express train were to overtake the goods train while moving in the same direction, then how long would it take to do so? (Assume that the trains continue to travel at the same respective speeds as mentioned earlier.)a)170 secondsb)130 secondsc)150 secondsd)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer?.
An express train travelling at a speed of 72 km/hr crosses a goods train travelling at a speed of 45 km/hr in the opposite direction in half a minute. If the express train were to overtake the goods train while moving in the same direction, then how long would it take to do so? (Assume that the trains continue to travel at the same respective speeds as mentioned earlier.)a)170 secondsb)130 secondsc)150 secondsd)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about An express train travelling at a speed of 72 km/hr crosses a goods train travelling at a speed of 45 km/hr in the opposite direction in half a minute. If the express train were to overtake the goods train while moving in the same direction, then how long would it take to do so? (Assume that the trains continue to travel at the same respective speeds as mentioned earlier.)a)170 secondsb)130 secondsc)150 secondsd)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An express train travelling at a speed of 72 km/hr crosses a goods train travelling at a speed of 45 km/hr in the opposite direction in half a minute. If the express train were to overtake the goods train while moving in the same direction, then how long would it take to do so? (Assume that the trains continue to travel at the same respective speeds as mentioned earlier.)a)170 secondsb)130 secondsc)150 secondsd)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer?.
Solutions for An express train travelling at a speed of 72 km/hr crosses a goods train travelling at a speed of 45 km/hr in the opposite direction in half a minute. If the express train were to overtake the goods train while moving in the same direction, then how long would it take to do so? (Assume that the trains continue to travel at the same respective speeds as mentioned earlier.)a)170 secondsb)130 secondsc)150 secondsd)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT.
Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
Here you can find the meaning of An express train travelling at a speed of 72 km/hr crosses a goods train travelling at a speed of 45 km/hr in the opposite direction in half a minute. If the express train were to overtake the goods train while moving in the same direction, then how long would it take to do so? (Assume that the trains continue to travel at the same respective speeds as mentioned earlier.)a)170 secondsb)130 secondsc)150 secondsd)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
An express train travelling at a speed of 72 km/hr crosses a goods train travelling at a speed of 45 km/hr in the opposite direction in half a minute. If the express train were to overtake the goods train while moving in the same direction, then how long would it take to do so? (Assume that the trains continue to travel at the same respective speeds as mentioned earlier.)a)170 secondsb)130 secondsc)150 secondsd)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for An express train travelling at a speed of 72 km/hr crosses a goods train travelling at a speed of 45 km/hr in the opposite direction in half a minute. If the express train were to overtake the goods train while moving in the same direction, then how long would it take to do so? (Assume that the trains continue to travel at the same respective speeds as mentioned earlier.)a)170 secondsb)130 secondsc)150 secondsd)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of An express train travelling at a speed of 72 km/hr crosses a goods train travelling at a speed of 45 km/hr in the opposite direction in half a minute. If the express train were to overtake the goods train while moving in the same direction, then how long would it take to do so? (Assume that the trains continue to travel at the same respective speeds as mentioned earlier.)a)170 secondsb)130 secondsc)150 secondsd)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice An express train travelling at a speed of 72 km/hr crosses a goods train travelling at a speed of 45 km/hr in the opposite direction in half a minute. If the express train were to overtake the goods train while moving in the same direction, then how long would it take to do so? (Assume that the trains continue to travel at the same respective speeds as mentioned earlier.)a)170 secondsb)130 secondsc)150 secondsd)Cannot be determinedCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice CAT tests.
|
|
Explore Courses for CAT exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup