SAT Exam > SAT Questions > The function f is a quadratic function with z...
Start Learning for Free
The function f is a quadratic function with zeros at x = 1 and x = 5. The graph of y = f(x) in the xy-plane is a parabola with a vertex at (3, -2). What is the y-intercept of this graph?
Correct answer is '2.5'. Can you explain this answer?
Most Upvoted Answer
The function f is a quadratic function with zeros at x = 1 and x = 5. ...
Using the Factor Theorem, we know that if a quadratic has zeroes at x = 1 and x = 5, it must have factors of (x - 1) and (x - 5). Since a quadratic can only have two linear factors, fmust be of the form f(x) = k(x - 1)(x - 5).
Substitute x = 3 and y = -2 for the f(x) = k(x - 1)(x - 5).
Substitute x = 3 and y = -2 for the coordinates of vertex: -2 = k(3 - 1)(3 - 5)
Simplify: -2 = k(2)(-2)
Simplify: -2 = -4k
Divide by -4: 1/2 = k
Therefore the equation of the function is
and we can find its y-intercept by substituting x = 0: 
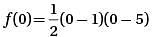
Simplify: f(0) = 5/2 or 2.5
Substitute x = 3 and y = -2 for the f(x) = k(x - 1)(x - 5).
Substitute x = 3 and y = -2 for the coordinates of vertex: -2 = k(3 - 1)(3 - 5)
Simplify: -2 = k(2)(-2)
Simplify: -2 = -4k
Divide by -4: 1/2 = k
Therefore the equation of the function is
and we can find its y-intercept by substituting x = 0: 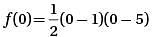Simplify: f(0) = 5/2 or 2.5
Free Test
FREE
| Start Free Test |
Community Answer
The function f is a quadratic function with zeros at x = 1 and x = 5. ...
Understanding the Quadratic Function
To find the y-intercept of the quadratic function f with the given characteristics, we can start by expressing the function using its roots and vertex.
1. Forming the Quadratic Equation
- The zeros (roots) of the function are at x = 1 and x = 5.
- Thus, the function can be expressed as:
f(x) = a(x - 1)(x - 5)
- The vertex is at (3, -2), which means f(3) = -2.
2. Finding the Coefficient 'a'
- Substitute x = 3 into the equation:
f(3) = a(3 - 1)(3 - 5)
f(3) = a(2)(-2) = -4a
- Set this equal to the vertex value:
-4a = -2
a = 0.5
3. The Complete Quadratic Function
- Now, substitute 'a' back into the function:
f(x) = 0.5(x - 1)(x - 5)
- Expanding this, we get:
f(x) = 0.5(x^2 - 6x + 5)
f(x) = 0.5x^2 - 3x + 2.5
4. Finding the Y-Intercept
- The y-intercept occurs when x = 0:
f(0) = 0.5(0)^2 - 3(0) + 2.5
f(0) = 2.5
Thus, the y-intercept of the graph is 2.5, confirming the correct answer.
To find the y-intercept of the quadratic function f with the given characteristics, we can start by expressing the function using its roots and vertex.
1. Forming the Quadratic Equation
- The zeros (roots) of the function are at x = 1 and x = 5.
- Thus, the function can be expressed as:
f(x) = a(x - 1)(x - 5)
- The vertex is at (3, -2), which means f(3) = -2.
2. Finding the Coefficient 'a'
- Substitute x = 3 into the equation:
f(3) = a(3 - 1)(3 - 5)
f(3) = a(2)(-2) = -4a
- Set this equal to the vertex value:
-4a = -2
a = 0.5
3. The Complete Quadratic Function
- Now, substitute 'a' back into the function:
f(x) = 0.5(x - 1)(x - 5)
- Expanding this, we get:
f(x) = 0.5(x^2 - 6x + 5)
f(x) = 0.5x^2 - 3x + 2.5
4. Finding the Y-Intercept
- The y-intercept occurs when x = 0:
f(0) = 0.5(0)^2 - 3(0) + 2.5
f(0) = 2.5
Thus, the y-intercept of the graph is 2.5, confirming the correct answer.
|
Explore Courses for SAT exam
|
|
Similar SAT Doubts
Top Courses for SATView all
The function f is a quadratic function with zeros at x = 1 and x = 5. The graph of y = f(x) in the xy-plane is a parabola with a vertex at (3, -2). What is the y-intercept of this graph?Correct answer is '2.5'. Can you explain this answer?
Question Description
The function f is a quadratic function with zeros at x = 1 and x = 5. The graph of y = f(x) in the xy-plane is a parabola with a vertex at (3, -2). What is the y-intercept of this graph?Correct answer is '2.5'. Can you explain this answer? for SAT 2025 is part of SAT preparation. The Question and answers have been prepared according to the SAT exam syllabus. Information about The function f is a quadratic function with zeros at x = 1 and x = 5. The graph of y = f(x) in the xy-plane is a parabola with a vertex at (3, -2). What is the y-intercept of this graph?Correct answer is '2.5'. Can you explain this answer? covers all topics & solutions for SAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The function f is a quadratic function with zeros at x = 1 and x = 5. The graph of y = f(x) in the xy-plane is a parabola with a vertex at (3, -2). What is the y-intercept of this graph?Correct answer is '2.5'. Can you explain this answer?.
The function f is a quadratic function with zeros at x = 1 and x = 5. The graph of y = f(x) in the xy-plane is a parabola with a vertex at (3, -2). What is the y-intercept of this graph?Correct answer is '2.5'. Can you explain this answer? for SAT 2025 is part of SAT preparation. The Question and answers have been prepared according to the SAT exam syllabus. Information about The function f is a quadratic function with zeros at x = 1 and x = 5. The graph of y = f(x) in the xy-plane is a parabola with a vertex at (3, -2). What is the y-intercept of this graph?Correct answer is '2.5'. Can you explain this answer? covers all topics & solutions for SAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The function f is a quadratic function with zeros at x = 1 and x = 5. The graph of y = f(x) in the xy-plane is a parabola with a vertex at (3, -2). What is the y-intercept of this graph?Correct answer is '2.5'. Can you explain this answer?.
Solutions for The function f is a quadratic function with zeros at x = 1 and x = 5. The graph of y = f(x) in the xy-plane is a parabola with a vertex at (3, -2). What is the y-intercept of this graph?Correct answer is '2.5'. Can you explain this answer? in English & in Hindi are available as part of our courses for SAT.
Download more important topics, notes, lectures and mock test series for SAT Exam by signing up for free.
Here you can find the meaning of The function f is a quadratic function with zeros at x = 1 and x = 5. The graph of y = f(x) in the xy-plane is a parabola with a vertex at (3, -2). What is the y-intercept of this graph?Correct answer is '2.5'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The function f is a quadratic function with zeros at x = 1 and x = 5. The graph of y = f(x) in the xy-plane is a parabola with a vertex at (3, -2). What is the y-intercept of this graph?Correct answer is '2.5'. Can you explain this answer?, a detailed solution for The function f is a quadratic function with zeros at x = 1 and x = 5. The graph of y = f(x) in the xy-plane is a parabola with a vertex at (3, -2). What is the y-intercept of this graph?Correct answer is '2.5'. Can you explain this answer? has been provided alongside types of The function f is a quadratic function with zeros at x = 1 and x = 5. The graph of y = f(x) in the xy-plane is a parabola with a vertex at (3, -2). What is the y-intercept of this graph?Correct answer is '2.5'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The function f is a quadratic function with zeros at x = 1 and x = 5. The graph of y = f(x) in the xy-plane is a parabola with a vertex at (3, -2). What is the y-intercept of this graph?Correct answer is '2.5'. Can you explain this answer? tests, examples and also practice SAT tests.
|
|
Explore Courses for SAT exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup