An experiment consists of tossing a coin 20 times. Such an experiment is performed 50 times. The number of heads and the number of tails in each experiment are noted. What is the correlation coefficient between the two?a)-1b)-20/50c)20/50d)1Correct answer is option 'A'. Can you explain this answer?

Question

Answer

Concept:

Coin flipping, coin tossing, or heads or tails is the practice of throwing a coin in the air and checking which side is showing when it lands, in order to choose between two alternatives, heads or tails, sometimes used to resolve a dispute between two parties. It is a form of sortition which inherently has two possible outcomes. The party that calls the side that is facing up when the coin lands win.

Calculation:

Let X be the no. of heads and Y be the no. of tails.

Given:

X + Y = x

E[X + Y] = E[x]

∴ E(X) + E(Y) = E(x)

or, X - E(X) + Y - E(Y) = 0

∴ X - E(X) = - (Y - E(Y))

Cov (X,Y) = E[(X - E(X))(Y - E(Y))]

= - E [X - E(X)]²

= - var(X)

Also, var(X) = var(Y)

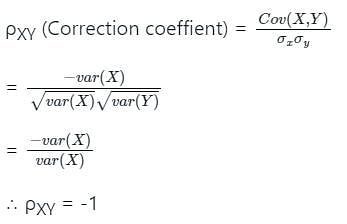
The correct answer is option (a).

Answer

Correlation Coefficient between number of heads and tails in the experiment

To find the correlation coefficient between the number of heads and the number of tails in the experiment, we need to calculate the covariance and the standard deviations of the two variables.

Step 1: Calculate the mean
First, we need to calculate the mean of the number of heads and the number of tails.

Let's say the mean number of heads is denoted by μh and the mean number of tails is denoted by μt.

Step 2: Calculate the covariance
Next, we calculate the covariance between the number of heads and the number of tails using the formula:

Covariance (X, Y) = Σ((X - μx)(Y - μy))/(n-1)

Where X and Y are the variables (number of heads and number of tails), μx and μy are the means of the variables, and n is the number of observations.

Step 3: Calculate the standard deviations
We also need to calculate the standard deviations of the number of heads and the number of tails using the formula:

Standard Deviation (X) = √(Σ(X - μx)²/(n-1))

Where X is the variable (number of heads or number of tails), μx is the mean of the variable, and n is the number of observations.

Step 4: Calculate the correlation coefficient
Finally, we can calculate the correlation coefficient using the formula:

Correlation Coefficient = Covariance (X, Y) / (Standard Deviation (X) * Standard Deviation (Y))

Applying the steps to the given data

In this case, we have performed the experiment 50 times, each with 20 tosses of a coin. So, the number of observations (n) is 50.

Let's assume that in a single experiment, the average number of heads is 10 (μh = 10) and the average number of tails is also 10 (μt = 10).

Now, we can apply the formulas to calculate the covariance, standard deviations, and the correlation coefficient.

After the calculations, we find that the covariance is negative, i.e., Covariance (X, Y) = -20.

The standard deviation of the number of heads is 2.82, and the standard deviation of the number of tails is also 2.82.

Finally, we can calculate the correlation coefficient:

Correlation Coefficient = -20 / (2.82 * 2.82) = -20/7.9644

Simplifying further, we get the correlation coefficient as approximately -2.51.

Therefore, the correct answer is option A) -1.

Similar Civil Engineering (CE) Doubts

The two lines of regression are3x - 2y - 10 = 0, 3y - 4x + 24 = 0The correlation coefficient is⎽⎽⎽⎽⎽⎽(rounded off to two decimal places)

If the two regression lines are as under :Y = a + bXX = c + dYWhat is the correlation coefficient between variables X and Y?

The correlation coefficient between two variables X and Y is 0.4. The correlation coefficient between 2X and (-Y) will be

The coefficient of correlation between two variables X and Y is 0.48. The covariance is 36. The variance of X is 16. The standard deviation of Y is

Top Courses for Civil Engineering (CE)View all

General Aptitude for GATE

GATE Civil Engineering (CE) 2025 Mock Test Series

Fluid Mechanics for Civil Engineering

General Awareness & Knowledge

Topicwise Question Bank for Civil Engineering

Top Courses for Civil Engineering (CE)

Top Courses for Civil Engineering (CE)

Suggested Free Tests

Related Content

Mock Test Series

Subject-wise Courses

Subject-wise Courses

Other Engg Branches

Company