Class 7 Exam > Class 7 Questions > If we denote speed by Sdistance by Dand time ...
Start Learning for Free
If we denote speed by S distance by D and time by T the relationship these equation is?
- a)S = D/T
- b)T = S/D
- c)S = D x T
- d)S = T/D
Correct answer is option 'A'. Can you explain this answer?
Verified Answer
If we denote speed by Sdistance by Dand time by Tthe relationship thes...
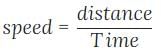
Most Upvoted Answer
If we denote speed by Sdistance by Dand time by Tthe relationship thes...
Explanation:
To understand the relationship between speed, distance, and time, let's break down the equation S = D/T.
Speed:
Speed is defined as the distance traveled per unit of time. It tells us how fast an object is moving. Speed is usually measured in units like meters per second (m/s) or kilometers per hour (km/h).
Distance:
Distance refers to the total length covered by an object. It is the actual path traveled by an object, and it is measured in units like meters (m), kilometers (km), or miles (mi).
Time:
Time measures the duration of an event or the interval between two events. In the context of speed, it refers to the time it takes for an object to travel a certain distance. Time can be measured in units like seconds (s), minutes (min), or hours (h).
Now, let's analyze the equation S = D/T:
S = D/T:
This equation states that speed (S) is equal to the distance (D) traveled divided by the time (T) taken to cover that distance.
Explanation of the equation:
- When we divide the distance by time, we obtain the speed. This means that speed is directly proportional to the distance traveled and inversely proportional to the time taken.
- If the distance traveled increases while the time taken remains constant, the speed will increase.
- Conversely, if the distance traveled remains constant while the time taken increases, the speed will decrease.
- The equation can also be rearranged to find the values of distance and time. For example, if we know the speed and time, we can calculate the distance by rearranging the equation as D = S x T.
Therefore, the correct relationship between speed (S), distance (D), and time (T) is S = D/T, as stated in option 'A'.
To understand the relationship between speed, distance, and time, let's break down the equation S = D/T.
Speed:
Speed is defined as the distance traveled per unit of time. It tells us how fast an object is moving. Speed is usually measured in units like meters per second (m/s) or kilometers per hour (km/h).
Distance:
Distance refers to the total length covered by an object. It is the actual path traveled by an object, and it is measured in units like meters (m), kilometers (km), or miles (mi).
Time:
Time measures the duration of an event or the interval between two events. In the context of speed, it refers to the time it takes for an object to travel a certain distance. Time can be measured in units like seconds (s), minutes (min), or hours (h).
Now, let's analyze the equation S = D/T:
S = D/T:
This equation states that speed (S) is equal to the distance (D) traveled divided by the time (T) taken to cover that distance.
Explanation of the equation:
- When we divide the distance by time, we obtain the speed. This means that speed is directly proportional to the distance traveled and inversely proportional to the time taken.
- If the distance traveled increases while the time taken remains constant, the speed will increase.
- Conversely, if the distance traveled remains constant while the time taken increases, the speed will decrease.
- The equation can also be rearranged to find the values of distance and time. For example, if we know the speed and time, we can calculate the distance by rearranging the equation as D = S x T.
Therefore, the correct relationship between speed (S), distance (D), and time (T) is S = D/T, as stated in option 'A'.
|
Explore Courses for Class 7 exam
|
|
Top Courses for Class 7View all
If we denote speed by Sdistance by Dand time by Tthe relationship these equation is?a)S = D/Tb)T = S/Dc)S = D x Td)S = T/DCorrect answer is option 'A'. Can you explain this answer?
Question Description
If we denote speed by Sdistance by Dand time by Tthe relationship these equation is?a)S = D/Tb)T = S/Dc)S = D x Td)S = T/DCorrect answer is option 'A'. Can you explain this answer? for Class 7 2025 is part of Class 7 preparation. The Question and answers have been prepared according to the Class 7 exam syllabus. Information about If we denote speed by Sdistance by Dand time by Tthe relationship these equation is?a)S = D/Tb)T = S/Dc)S = D x Td)S = T/DCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Class 7 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If we denote speed by Sdistance by Dand time by Tthe relationship these equation is?a)S = D/Tb)T = S/Dc)S = D x Td)S = T/DCorrect answer is option 'A'. Can you explain this answer?.
If we denote speed by Sdistance by Dand time by Tthe relationship these equation is?a)S = D/Tb)T = S/Dc)S = D x Td)S = T/DCorrect answer is option 'A'. Can you explain this answer? for Class 7 2025 is part of Class 7 preparation. The Question and answers have been prepared according to the Class 7 exam syllabus. Information about If we denote speed by Sdistance by Dand time by Tthe relationship these equation is?a)S = D/Tb)T = S/Dc)S = D x Td)S = T/DCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Class 7 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If we denote speed by Sdistance by Dand time by Tthe relationship these equation is?a)S = D/Tb)T = S/Dc)S = D x Td)S = T/DCorrect answer is option 'A'. Can you explain this answer?.
Solutions for If we denote speed by Sdistance by Dand time by Tthe relationship these equation is?a)S = D/Tb)T = S/Dc)S = D x Td)S = T/DCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 7.
Download more important topics, notes, lectures and mock test series for Class 7 Exam by signing up for free.
Here you can find the meaning of If we denote speed by Sdistance by Dand time by Tthe relationship these equation is?a)S = D/Tb)T = S/Dc)S = D x Td)S = T/DCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
If we denote speed by Sdistance by Dand time by Tthe relationship these equation is?a)S = D/Tb)T = S/Dc)S = D x Td)S = T/DCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for If we denote speed by Sdistance by Dand time by Tthe relationship these equation is?a)S = D/Tb)T = S/Dc)S = D x Td)S = T/DCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of If we denote speed by Sdistance by Dand time by Tthe relationship these equation is?a)S = D/Tb)T = S/Dc)S = D x Td)S = T/DCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice If we denote speed by Sdistance by Dand time by Tthe relationship these equation is?a)S = D/Tb)T = S/Dc)S = D x Td)S = T/DCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Class 7 tests.
|
|
Explore Courses for Class 7 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup