Electronics and Communication Engineering (ECE) Exam > Electronics and Communication Engineering (ECE) Questions > Let X(t) be a wide sense stationary random pr...
Start Learning for Free
Let X(t) be a wide sense stationary random process with the power spectral density SX(f) as shown in Figure (a), where f is in Hertz (Hz). The random process X(t) is input to an ideal lowpass filter with the frequency response:
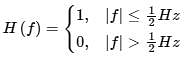
This is as shown in Figure (b). The output of the lowpass filter is Y(t).
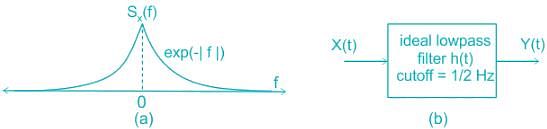
Let E be the expectation operator. Consider the following statements:
I. E(X(t)) = E(Y(t))
II. E(X2(t)) = E(Y2(t))
III. E(Y2(t)) = 2
Select the correct option:
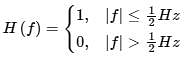
This is as shown in Figure (b). The output of the lowpass filter is Y(t).
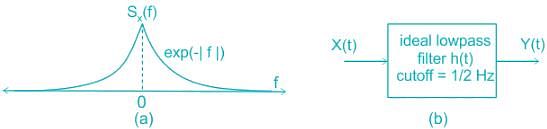
Let E be the expectation operator. Consider the following statements:
I. E(X(t)) = E(Y(t))
II. E(X2(t)) = E(Y2(t))
III. E(Y2(t)) = 2
Select the correct option:
- a)only I is true
- b)only II and III are true
- c)only I and II are true
- d)only I and III are true
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
Let X(t) be a wide sense stationary random process with the power spec...
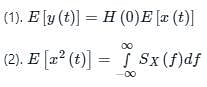
Application:
In the given question,
H(0) = 1
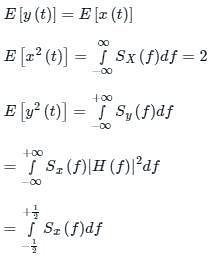
2 - 2 e-0.5
Low pass filter does not allow total power to pass from input to output.
Hence,
E[X2(t)] ≠ E[Y2(t)]
Attention Electronics and Communication Engineering (ECE) Students!
To make sure you are not studying endlessly, EduRev has designed Electronics and Communication Engineering (ECE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Electronics and Communication Engineering (ECE).

|
Explore Courses for Electronics and Communication Engineering (ECE) exam
|

|
Similar Electronics and Communication Engineering (ECE) Doubts
Let X(t) be a wide sense stationary random process with the power spectral density SX(f) as shown in Figure (a), where f is in Hertz (Hz). The random process X(t) is input to an ideal lowpass filter with the frequency response:This is as shown in Figure (b). The output of the lowpass filter is Y(t).Let E be the expectation operator. Consider the following statements:I. E(X(t)) = E(Y(t))II. E(X2(t)) = E(Y2(t))III. E(Y2(t)) = 2Select the correct option:a)only I is trueb)only II and III are truec)only I and II are trued)only I and III are trueCorrect answer is option 'A'. Can you explain this answer?
Question Description
Let X(t) be a wide sense stationary random process with the power spectral density SX(f) as shown in Figure (a), where f is in Hertz (Hz). The random process X(t) is input to an ideal lowpass filter with the frequency response:This is as shown in Figure (b). The output of the lowpass filter is Y(t).Let E be the expectation operator. Consider the following statements:I. E(X(t)) = E(Y(t))II. E(X2(t)) = E(Y2(t))III. E(Y2(t)) = 2Select the correct option:a)only I is trueb)only II and III are truec)only I and II are trued)only I and III are trueCorrect answer is option 'A'. Can you explain this answer? for Electronics and Communication Engineering (ECE) 2024 is part of Electronics and Communication Engineering (ECE) preparation. The Question and answers have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. Information about Let X(t) be a wide sense stationary random process with the power spectral density SX(f) as shown in Figure (a), where f is in Hertz (Hz). The random process X(t) is input to an ideal lowpass filter with the frequency response:This is as shown in Figure (b). The output of the lowpass filter is Y(t).Let E be the expectation operator. Consider the following statements:I. E(X(t)) = E(Y(t))II. E(X2(t)) = E(Y2(t))III. E(Y2(t)) = 2Select the correct option:a)only I is trueb)only II and III are truec)only I and II are trued)only I and III are trueCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Electronics and Communication Engineering (ECE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Let X(t) be a wide sense stationary random process with the power spectral density SX(f) as shown in Figure (a), where f is in Hertz (Hz). The random process X(t) is input to an ideal lowpass filter with the frequency response:This is as shown in Figure (b). The output of the lowpass filter is Y(t).Let E be the expectation operator. Consider the following statements:I. E(X(t)) = E(Y(t))II. E(X2(t)) = E(Y2(t))III. E(Y2(t)) = 2Select the correct option:a)only I is trueb)only II and III are truec)only I and II are trued)only I and III are trueCorrect answer is option 'A'. Can you explain this answer?.
Let X(t) be a wide sense stationary random process with the power spectral density SX(f) as shown in Figure (a), where f is in Hertz (Hz). The random process X(t) is input to an ideal lowpass filter with the frequency response:This is as shown in Figure (b). The output of the lowpass filter is Y(t).Let E be the expectation operator. Consider the following statements:I. E(X(t)) = E(Y(t))II. E(X2(t)) = E(Y2(t))III. E(Y2(t)) = 2Select the correct option:a)only I is trueb)only II and III are truec)only I and II are trued)only I and III are trueCorrect answer is option 'A'. Can you explain this answer? for Electronics and Communication Engineering (ECE) 2024 is part of Electronics and Communication Engineering (ECE) preparation. The Question and answers have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. Information about Let X(t) be a wide sense stationary random process with the power spectral density SX(f) as shown in Figure (a), where f is in Hertz (Hz). The random process X(t) is input to an ideal lowpass filter with the frequency response:This is as shown in Figure (b). The output of the lowpass filter is Y(t).Let E be the expectation operator. Consider the following statements:I. E(X(t)) = E(Y(t))II. E(X2(t)) = E(Y2(t))III. E(Y2(t)) = 2Select the correct option:a)only I is trueb)only II and III are truec)only I and II are trued)only I and III are trueCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Electronics and Communication Engineering (ECE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Let X(t) be a wide sense stationary random process with the power spectral density SX(f) as shown in Figure (a), where f is in Hertz (Hz). The random process X(t) is input to an ideal lowpass filter with the frequency response:This is as shown in Figure (b). The output of the lowpass filter is Y(t).Let E be the expectation operator. Consider the following statements:I. E(X(t)) = E(Y(t))II. E(X2(t)) = E(Y2(t))III. E(Y2(t)) = 2Select the correct option:a)only I is trueb)only II and III are truec)only I and II are trued)only I and III are trueCorrect answer is option 'A'. Can you explain this answer?.
Solutions for Let X(t) be a wide sense stationary random process with the power spectral density SX(f) as shown in Figure (a), where f is in Hertz (Hz). The random process X(t) is input to an ideal lowpass filter with the frequency response:This is as shown in Figure (b). The output of the lowpass filter is Y(t).Let E be the expectation operator. Consider the following statements:I. E(X(t)) = E(Y(t))II. E(X2(t)) = E(Y2(t))III. E(Y2(t)) = 2Select the correct option:a)only I is trueb)only II and III are truec)only I and II are trued)only I and III are trueCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electronics and Communication Engineering (ECE).
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free.
Here you can find the meaning of Let X(t) be a wide sense stationary random process with the power spectral density SX(f) as shown in Figure (a), where f is in Hertz (Hz). The random process X(t) is input to an ideal lowpass filter with the frequency response:This is as shown in Figure (b). The output of the lowpass filter is Y(t).Let E be the expectation operator. Consider the following statements:I. E(X(t)) = E(Y(t))II. E(X2(t)) = E(Y2(t))III. E(Y2(t)) = 2Select the correct option:a)only I is trueb)only II and III are truec)only I and II are trued)only I and III are trueCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Let X(t) be a wide sense stationary random process with the power spectral density SX(f) as shown in Figure (a), where f is in Hertz (Hz). The random process X(t) is input to an ideal lowpass filter with the frequency response:This is as shown in Figure (b). The output of the lowpass filter is Y(t).Let E be the expectation operator. Consider the following statements:I. E(X(t)) = E(Y(t))II. E(X2(t)) = E(Y2(t))III. E(Y2(t)) = 2Select the correct option:a)only I is trueb)only II and III are truec)only I and II are trued)only I and III are trueCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for Let X(t) be a wide sense stationary random process with the power spectral density SX(f) as shown in Figure (a), where f is in Hertz (Hz). The random process X(t) is input to an ideal lowpass filter with the frequency response:This is as shown in Figure (b). The output of the lowpass filter is Y(t).Let E be the expectation operator. Consider the following statements:I. E(X(t)) = E(Y(t))II. E(X2(t)) = E(Y2(t))III. E(Y2(t)) = 2Select the correct option:a)only I is trueb)only II and III are truec)only I and II are trued)only I and III are trueCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of Let X(t) be a wide sense stationary random process with the power spectral density SX(f) as shown in Figure (a), where f is in Hertz (Hz). The random process X(t) is input to an ideal lowpass filter with the frequency response:This is as shown in Figure (b). The output of the lowpass filter is Y(t).Let E be the expectation operator. Consider the following statements:I. E(X(t)) = E(Y(t))II. E(X2(t)) = E(Y2(t))III. E(Y2(t)) = 2Select the correct option:a)only I is trueb)only II and III are truec)only I and II are trued)only I and III are trueCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Let X(t) be a wide sense stationary random process with the power spectral density SX(f) as shown in Figure (a), where f is in Hertz (Hz). The random process X(t) is input to an ideal lowpass filter with the frequency response:This is as shown in Figure (b). The output of the lowpass filter is Y(t).Let E be the expectation operator. Consider the following statements:I. E(X(t)) = E(Y(t))II. E(X2(t)) = E(Y2(t))III. E(Y2(t)) = 2Select the correct option:a)only I is trueb)only II and III are truec)only I and II are trued)only I and III are trueCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Electronics and Communication Engineering (ECE) tests.

|
Explore Courses for Electronics and Communication Engineering (ECE) exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























