UGC NET Exam > UGC NET Questions > Assume that the noise spectral density at any...
Start Learning for Free
Assume that the noise spectral density at any given frequency, in a current amplifier is independent of frequency. The bandwidth of measurement is changed from 2 Hz to 30 Hz. The ratio (B/A) of the RMS noise current before (A) and after (B) the bandwidth modification?
- a)0.26
- b)1.87
- c)3.87
- d)5.27
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
Assume that the noise spectral density at any given frequency, in a cu...
Problem Analysis:
We are given that the noise spectral density at any given frequency in a current amplifier is independent of frequency. We need to find the ratio of the RMS noise current before and after the bandwidth modification.
Solution:
Step 1: Understanding the Problem
To solve this problem, we need to understand the concept of noise spectral density and RMS noise current.
Step 2: Understanding Noise Spectral Density
Noise spectral density represents the amount of noise present at each frequency in a system. In this problem, we are given that the noise spectral density is independent of frequency. This means that the noise power is spread equally over all frequencies.
Step 3: Understanding RMS Noise Current
RMS noise current is a measure of the average noise current in a system. It is calculated by taking the square root of the integral of the noise spectral density over the bandwidth of the measurement.
Step 4: Calculating the Ratio of RMS Noise Current
We are given that the bandwidth of measurement is changed from 2 Hz to 30 Hz. To calculate the ratio of RMS noise current before and after the bandwidth modification, we need to compare the RMS noise current in the two cases.
Let's assume the RMS noise current before the bandwidth modification as A, and after the bandwidth modification as B.
Since the noise spectral density is independent of frequency, the noise power is spread equally over all frequencies. Therefore, the RMS noise current is directly proportional to the square root of the bandwidth.
Step 5: Applying the Formula
The ratio of the RMS noise current before and after the bandwidth modification can be calculated using the formula:
(B/A) = sqrt(B2/A2) = sqrt(30/2) = sqrt(15) ≈ 3.87
Step 6: Final Answer
Therefore, the ratio of the RMS noise current before and after the bandwidth modification is approximately 3.87.
Conclusion:
The ratio of the RMS noise current before and after the bandwidth modification is approximately 3.87.
We are given that the noise spectral density at any given frequency in a current amplifier is independent of frequency. We need to find the ratio of the RMS noise current before and after the bandwidth modification.
Solution:
Step 1: Understanding the Problem
To solve this problem, we need to understand the concept of noise spectral density and RMS noise current.
Step 2: Understanding Noise Spectral Density
Noise spectral density represents the amount of noise present at each frequency in a system. In this problem, we are given that the noise spectral density is independent of frequency. This means that the noise power is spread equally over all frequencies.
Step 3: Understanding RMS Noise Current
RMS noise current is a measure of the average noise current in a system. It is calculated by taking the square root of the integral of the noise spectral density over the bandwidth of the measurement.
Step 4: Calculating the Ratio of RMS Noise Current
We are given that the bandwidth of measurement is changed from 2 Hz to 30 Hz. To calculate the ratio of RMS noise current before and after the bandwidth modification, we need to compare the RMS noise current in the two cases.
Let's assume the RMS noise current before the bandwidth modification as A, and after the bandwidth modification as B.
Since the noise spectral density is independent of frequency, the noise power is spread equally over all frequencies. Therefore, the RMS noise current is directly proportional to the square root of the bandwidth.
Step 5: Applying the Formula
The ratio of the RMS noise current before and after the bandwidth modification can be calculated using the formula:
(B/A) = sqrt(B2/A2) = sqrt(30/2) = sqrt(15) ≈ 3.87
Step 6: Final Answer
Therefore, the ratio of the RMS noise current before and after the bandwidth modification is approximately 3.87.
Conclusion:
The ratio of the RMS noise current before and after the bandwidth modification is approximately 3.87.
Free Test
FREE
| Start Free Test |
Community Answer
Assume that the noise spectral density at any given frequency, in a cu...
In communications, noise spectral density (NSD), noise power density, noise power spectral density, or simply noise density (N0) is the power spectral density of noise or the noise power per unit of bandwidth. It has dimension of power over frequency, whose SI unit is watt per hertz (equivalent to watt-second or joule). It is commonly used in link budgets as the denominator of the important figure-of-merit ratios, such as carrier-to-noise-density ratio as well as Eb/N0 and Es/N0.
If the noise is one-sided white noise, i.e., constant with frequency, then the total noise power N integrated over a bandwidth B is N = BN0 (for double-sided white noise, the bandwidth is doubled, so N is BN0/2). This is utilized in signal-to-noise ratio calculations.
For thermal noise, its spectral density is given by N0 = kT, where k is the Boltzmann constant in joules per kelvin, and T is the receiver system noise temperature in kelvins.
The noise amplitude spectral density is the square root of the noise power spectral density, and is given in units such as
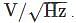
Explanation:
In the general opamp noise spectrum, we have two regions one is pink region.
This is when the spectrum is dependent on frequency whereas,
the other one is where the spectrum is independent of frequency which we call as white noise.
Now we are given with the condition that the noise spectral density at any given frequency, in a current amplifier is independent of frequency.
So, we have the rms noise spectral density to be:
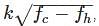
The noise amplitude spectral density is the square root of the noise power spectral density, and is given in units such as
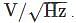
Explanation:
In the general opamp noise spectrum, we have two regions one is pink region.
This is when the spectrum is dependent on frequency whereas,
the other one is where the spectrum is independent of frequency which we call as white noise.
Now we are given with the condition that the noise spectral density at any given frequency, in a current amplifier is independent of frequency.
So, we have the rms noise spectral density to be:
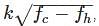
where fc is the lower limit of frequency in this white region where as fh is the higher frequency limit.
We are given with the difference in lower and higher frequency before the modification to be 2Hz.
Therefore:
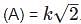
(B) which is after modification gives: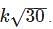
The ratio is given as B/A:
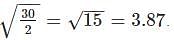
We are given with the difference in lower and higher frequency before the modification to be 2Hz.
Therefore:
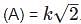
(B) which is after modification gives:
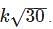
The ratio is given as B/A:
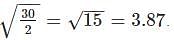
Attention UGC NET Students!
To make sure you are not studying endlessly, EduRev has designed UGC NET study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in UGC NET.

|
Explore Courses for UGC NET exam
|

|
Similar UGC NET Doubts
Assume that the noise spectral density at any given frequency, in a current amplifier is independent of frequency. The bandwidth of measurement is changed from 2 Hz to 30 Hz. The ratio (B/A) of the RMS noise current before (A) and after (B) the bandwidth modification?a)0.26b)1.87c)3.87d)5.27Correct answer is option 'C'. Can you explain this answer?
Question Description
Assume that the noise spectral density at any given frequency, in a current amplifier is independent of frequency. The bandwidth of measurement is changed from 2 Hz to 30 Hz. The ratio (B/A) of the RMS noise current before (A) and after (B) the bandwidth modification?a)0.26b)1.87c)3.87d)5.27Correct answer is option 'C'. Can you explain this answer? for UGC NET 2024 is part of UGC NET preparation. The Question and answers have been prepared according to the UGC NET exam syllabus. Information about Assume that the noise spectral density at any given frequency, in a current amplifier is independent of frequency. The bandwidth of measurement is changed from 2 Hz to 30 Hz. The ratio (B/A) of the RMS noise current before (A) and after (B) the bandwidth modification?a)0.26b)1.87c)3.87d)5.27Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for UGC NET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Assume that the noise spectral density at any given frequency, in a current amplifier is independent of frequency. The bandwidth of measurement is changed from 2 Hz to 30 Hz. The ratio (B/A) of the RMS noise current before (A) and after (B) the bandwidth modification?a)0.26b)1.87c)3.87d)5.27Correct answer is option 'C'. Can you explain this answer?.
Assume that the noise spectral density at any given frequency, in a current amplifier is independent of frequency. The bandwidth of measurement is changed from 2 Hz to 30 Hz. The ratio (B/A) of the RMS noise current before (A) and after (B) the bandwidth modification?a)0.26b)1.87c)3.87d)5.27Correct answer is option 'C'. Can you explain this answer? for UGC NET 2024 is part of UGC NET preparation. The Question and answers have been prepared according to the UGC NET exam syllabus. Information about Assume that the noise spectral density at any given frequency, in a current amplifier is independent of frequency. The bandwidth of measurement is changed from 2 Hz to 30 Hz. The ratio (B/A) of the RMS noise current before (A) and after (B) the bandwidth modification?a)0.26b)1.87c)3.87d)5.27Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for UGC NET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Assume that the noise spectral density at any given frequency, in a current amplifier is independent of frequency. The bandwidth of measurement is changed from 2 Hz to 30 Hz. The ratio (B/A) of the RMS noise current before (A) and after (B) the bandwidth modification?a)0.26b)1.87c)3.87d)5.27Correct answer is option 'C'. Can you explain this answer?.
Solutions for Assume that the noise spectral density at any given frequency, in a current amplifier is independent of frequency. The bandwidth of measurement is changed from 2 Hz to 30 Hz. The ratio (B/A) of the RMS noise current before (A) and after (B) the bandwidth modification?a)0.26b)1.87c)3.87d)5.27Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for UGC NET.
Download more important topics, notes, lectures and mock test series for UGC NET Exam by signing up for free.
Here you can find the meaning of Assume that the noise spectral density at any given frequency, in a current amplifier is independent of frequency. The bandwidth of measurement is changed from 2 Hz to 30 Hz. The ratio (B/A) of the RMS noise current before (A) and after (B) the bandwidth modification?a)0.26b)1.87c)3.87d)5.27Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Assume that the noise spectral density at any given frequency, in a current amplifier is independent of frequency. The bandwidth of measurement is changed from 2 Hz to 30 Hz. The ratio (B/A) of the RMS noise current before (A) and after (B) the bandwidth modification?a)0.26b)1.87c)3.87d)5.27Correct answer is option 'C'. Can you explain this answer?, a detailed solution for Assume that the noise spectral density at any given frequency, in a current amplifier is independent of frequency. The bandwidth of measurement is changed from 2 Hz to 30 Hz. The ratio (B/A) of the RMS noise current before (A) and after (B) the bandwidth modification?a)0.26b)1.87c)3.87d)5.27Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of Assume that the noise spectral density at any given frequency, in a current amplifier is independent of frequency. The bandwidth of measurement is changed from 2 Hz to 30 Hz. The ratio (B/A) of the RMS noise current before (A) and after (B) the bandwidth modification?a)0.26b)1.87c)3.87d)5.27Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Assume that the noise spectral density at any given frequency, in a current amplifier is independent of frequency. The bandwidth of measurement is changed from 2 Hz to 30 Hz. The ratio (B/A) of the RMS noise current before (A) and after (B) the bandwidth modification?a)0.26b)1.87c)3.87d)5.27Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice UGC NET tests.

|
Explore Courses for UGC NET exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























