Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > The shear stress in a circular pipe with a la...
Start Learning for Free
The shear stress in a circular pipe with a laminar flow in it
- a)varies parabolically across cross section
- b)varies inversely as the distance from mid plane
- c)remains constant over cross section
- d)varies directly as the distance from the mid plane
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
The shear stress in a circular pipe with a laminar flow in ita)varies ...
The correct answer is option 'D': The shear stress in a circular pipe with a laminar flow varies directly as the distance from the mid plane.
Explanation:
In fluid mechanics, shear stress refers to the force per unit area acting tangentially to a fluid flow. In a circular pipe with laminar flow, the flow profile is parabolic, meaning that the velocity of the fluid varies across the cross-section of the pipe.
When considering the shear stress distribution across the cross-section of the pipe, it is important to note that the velocity of the fluid is maximum at the center of the pipe (mid plane) and decreases towards the pipe walls.
The shear stress at any point within the fluid can be calculated using the equation:
τ = μ(dv/dr)
Where:
- τ is the shear stress
- μ is the dynamic viscosity of the fluid
- dv/dr is the velocity gradient, i.e., the rate of change of velocity with respect to the radial distance from the center of the pipe
Analysis:
To understand how shear stress varies across the cross-section of the pipe, let's consider a hypothetical point A at a distance r from the center of the pipe.
- At the center of the pipe (r = 0), the velocity gradient (dv/dr) is zero, and therefore the shear stress (τ) is also zero.
- As we move away from the center towards the wall of the pipe, the distance (r) increases, and the velocity gradient (dv/dr) also increases. This means that the shear stress (τ) increases as well.
- Hence, the shear stress varies directly with the distance from the mid plane.
This variation in shear stress can be represented by a linear relationship, where the shear stress is maximum at the pipe wall and zero at the center.
Conclusion:
In summary, the shear stress in a circular pipe with a laminar flow varies directly as the distance from the mid plane. This means that the shear stress increases linearly as the radial distance from the center of the pipe increases.
Explanation:
In fluid mechanics, shear stress refers to the force per unit area acting tangentially to a fluid flow. In a circular pipe with laminar flow, the flow profile is parabolic, meaning that the velocity of the fluid varies across the cross-section of the pipe.
When considering the shear stress distribution across the cross-section of the pipe, it is important to note that the velocity of the fluid is maximum at the center of the pipe (mid plane) and decreases towards the pipe walls.
The shear stress at any point within the fluid can be calculated using the equation:
τ = μ(dv/dr)
Where:
- τ is the shear stress
- μ is the dynamic viscosity of the fluid
- dv/dr is the velocity gradient, i.e., the rate of change of velocity with respect to the radial distance from the center of the pipe
Analysis:
To understand how shear stress varies across the cross-section of the pipe, let's consider a hypothetical point A at a distance r from the center of the pipe.
- At the center of the pipe (r = 0), the velocity gradient (dv/dr) is zero, and therefore the shear stress (τ) is also zero.
- As we move away from the center towards the wall of the pipe, the distance (r) increases, and the velocity gradient (dv/dr) also increases. This means that the shear stress (τ) increases as well.
- Hence, the shear stress varies directly with the distance from the mid plane.
This variation in shear stress can be represented by a linear relationship, where the shear stress is maximum at the pipe wall and zero at the center.
Conclusion:
In summary, the shear stress in a circular pipe with a laminar flow varies directly as the distance from the mid plane. This means that the shear stress increases linearly as the radial distance from the center of the pipe increases.
Free Test
FREE
| Start Free Test |
Community Answer
The shear stress in a circular pipe with a laminar flow in ita)varies ...
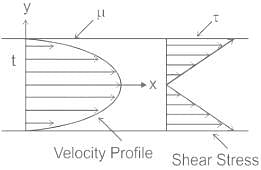
For a laminar flow through the circular pipe (Hagen-Poiseuille flow), shear stress (τ) distribution is given by:
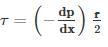
τ ⍺ r i.e. Shear stress is proportional to the radial distance from the centre of the pipe.
Therefore, for laminar flow through a round pipe, the shear stress varies linearly with the radial distance.
The negative sign on dp/dx depicts the decrease in the pressure in the direction of the flow. This is because the pressure must decrease because pressure force is the only means which is available to compensate for resistance to the flow.
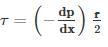
τ ⍺ r i.e. Shear stress is proportional to the radial distance from the centre of the pipe.
Therefore, for laminar flow through a round pipe, the shear stress varies linearly with the radial distance.
The negative sign on dp/dx depicts the decrease in the pressure in the direction of the flow. This is because the pressure must decrease because pressure force is the only means which is available to compensate for resistance to the flow.
Attention Civil Engineering (CE) Students!
To make sure you are not studying endlessly, EduRev has designed Civil Engineering (CE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Civil Engineering (CE).
|
Explore Courses for Civil Engineering (CE) exam
|
|
Similar Civil Engineering (CE) Doubts
Top Courses for Civil Engineering (CE)View all
The shear stress in a circular pipe with a laminar flow in ita)varies parabolically across cross sectionb)varies inversely as the distance from mid planec)remains constant over cross sectiond)varies directly as the distance from the mid planeCorrect answer is option 'D'. Can you explain this answer?
Question Description
The shear stress in a circular pipe with a laminar flow in ita)varies parabolically across cross sectionb)varies inversely as the distance from mid planec)remains constant over cross sectiond)varies directly as the distance from the mid planeCorrect answer is option 'D'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about The shear stress in a circular pipe with a laminar flow in ita)varies parabolically across cross sectionb)varies inversely as the distance from mid planec)remains constant over cross sectiond)varies directly as the distance from the mid planeCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The shear stress in a circular pipe with a laminar flow in ita)varies parabolically across cross sectionb)varies inversely as the distance from mid planec)remains constant over cross sectiond)varies directly as the distance from the mid planeCorrect answer is option 'D'. Can you explain this answer?.
The shear stress in a circular pipe with a laminar flow in ita)varies parabolically across cross sectionb)varies inversely as the distance from mid planec)remains constant over cross sectiond)varies directly as the distance from the mid planeCorrect answer is option 'D'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about The shear stress in a circular pipe with a laminar flow in ita)varies parabolically across cross sectionb)varies inversely as the distance from mid planec)remains constant over cross sectiond)varies directly as the distance from the mid planeCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The shear stress in a circular pipe with a laminar flow in ita)varies parabolically across cross sectionb)varies inversely as the distance from mid planec)remains constant over cross sectiond)varies directly as the distance from the mid planeCorrect answer is option 'D'. Can you explain this answer?.
Solutions for The shear stress in a circular pipe with a laminar flow in ita)varies parabolically across cross sectionb)varies inversely as the distance from mid planec)remains constant over cross sectiond)varies directly as the distance from the mid planeCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of The shear stress in a circular pipe with a laminar flow in ita)varies parabolically across cross sectionb)varies inversely as the distance from mid planec)remains constant over cross sectiond)varies directly as the distance from the mid planeCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The shear stress in a circular pipe with a laminar flow in ita)varies parabolically across cross sectionb)varies inversely as the distance from mid planec)remains constant over cross sectiond)varies directly as the distance from the mid planeCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for The shear stress in a circular pipe with a laminar flow in ita)varies parabolically across cross sectionb)varies inversely as the distance from mid planec)remains constant over cross sectiond)varies directly as the distance from the mid planeCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of The shear stress in a circular pipe with a laminar flow in ita)varies parabolically across cross sectionb)varies inversely as the distance from mid planec)remains constant over cross sectiond)varies directly as the distance from the mid planeCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The shear stress in a circular pipe with a laminar flow in ita)varies parabolically across cross sectionb)varies inversely as the distance from mid planec)remains constant over cross sectiond)varies directly as the distance from the mid planeCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.
|
|
Explore Courses for Civil Engineering (CE) exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup