Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > A clay layer 10 m thick in the field takes 40...
Start Learning for Free
A clay layer 10 m thick in the field takes 400 days to attain 50% consolidation with the condition of double drainage. If the same clay layer is underlain by a hard rock then the time taken to attain 50% consolidation is:
- a)100 days
- b)800 days
- c)1600 days
- d)200 days
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
A clay layer 10 m thick in the field takes 400 days to attain 50% cons...
The time required for any degree of consolidation can be obtained from Taylor's formula as
Where Cv = Coefficient of consolidation ( it is constant for the same type of soil)
Tv = Time factor ( it is also constant for the same degree of consolidation)
d = length of the drainage path
The time required for consolidation is directly proportional to the square of the length of the drainage path.
Given data and Calculation-
The field takes 400 days to attain 50% consolidation with the condition of double drainage.
The thickness of the clay layer = 10 m
For double drainage = d = 5 m
For single drainage = d = 10 m
From (1)
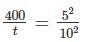
t = 1600 days
Where Cv = Coefficient of consolidation ( it is constant for the same type of soil)
Tv = Time factor ( it is also constant for the same degree of consolidation)
d = length of the drainage path
The time required for consolidation is directly proportional to the square of the length of the drainage path.
Given data and Calculation-
The field takes 400 days to attain 50% consolidation with the condition of double drainage.
The thickness of the clay layer = 10 m
For double drainage = d = 5 m
For single drainage = d = 10 m
From (1)
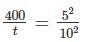
t = 1600 days
Most Upvoted Answer
A clay layer 10 m thick in the field takes 400 days to attain 50% cons...
Given Data:
- Clay layer thickness = 10 m
- Time taken for 50% consolidation with double drainage = 400 days
Explanation:
Consolidation process:
- Consolidation is the process by which soil decreases in volume due to the expulsion of water when loads are applied to it.
- The time taken for consolidation depends on factors such as soil type, layer thickness, drainage conditions, etc.
Effect of underlying hard rock:
- When a clay layer is underlain by a hard rock, the drainage conditions change.
- The presence of a hard rock layer restricts the drainage of water from the clay layer, leading to slower consolidation.
Calculation:
- The time taken for 50% consolidation with double drainage in the given scenario is 400 days.
- When the clay layer is underlain by a hard rock, the time taken for consolidation increases.
- The time taken for 50% consolidation in this case is calculated by multiplying the original time by a factor of 4 (as per Terzaghi's theory).
- Therefore, the time taken for 50% consolidation with an underlying hard rock is 4 * 400 = 1600 days.
Therefore, the correct answer is option C) 1600 days.
- Clay layer thickness = 10 m
- Time taken for 50% consolidation with double drainage = 400 days
Explanation:
Consolidation process:
- Consolidation is the process by which soil decreases in volume due to the expulsion of water when loads are applied to it.
- The time taken for consolidation depends on factors such as soil type, layer thickness, drainage conditions, etc.
Effect of underlying hard rock:
- When a clay layer is underlain by a hard rock, the drainage conditions change.
- The presence of a hard rock layer restricts the drainage of water from the clay layer, leading to slower consolidation.
Calculation:
- The time taken for 50% consolidation with double drainage in the given scenario is 400 days.
- When the clay layer is underlain by a hard rock, the time taken for consolidation increases.
- The time taken for 50% consolidation in this case is calculated by multiplying the original time by a factor of 4 (as per Terzaghi's theory).
- Therefore, the time taken for 50% consolidation with an underlying hard rock is 4 * 400 = 1600 days.
Therefore, the correct answer is option C) 1600 days.
|
Explore Courses for Civil Engineering (CE) exam
|
|
Similar Civil Engineering (CE) Doubts
Top Courses for Civil Engineering (CE)View all
A clay layer 10 m thick in the field takes 400 days to attain 50% consolidation with the condition of double drainage. If the same clay layer is underlain by a hard rock then the time taken to attain 50% consolidation is:a)100 daysb)800 daysc)1600 daysd)200 daysCorrect answer is option 'C'. Can you explain this answer?
Question Description
A clay layer 10 m thick in the field takes 400 days to attain 50% consolidation with the condition of double drainage. If the same clay layer is underlain by a hard rock then the time taken to attain 50% consolidation is:a)100 daysb)800 daysc)1600 daysd)200 daysCorrect answer is option 'C'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A clay layer 10 m thick in the field takes 400 days to attain 50% consolidation with the condition of double drainage. If the same clay layer is underlain by a hard rock then the time taken to attain 50% consolidation is:a)100 daysb)800 daysc)1600 daysd)200 daysCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A clay layer 10 m thick in the field takes 400 days to attain 50% consolidation with the condition of double drainage. If the same clay layer is underlain by a hard rock then the time taken to attain 50% consolidation is:a)100 daysb)800 daysc)1600 daysd)200 daysCorrect answer is option 'C'. Can you explain this answer?.
A clay layer 10 m thick in the field takes 400 days to attain 50% consolidation with the condition of double drainage. If the same clay layer is underlain by a hard rock then the time taken to attain 50% consolidation is:a)100 daysb)800 daysc)1600 daysd)200 daysCorrect answer is option 'C'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A clay layer 10 m thick in the field takes 400 days to attain 50% consolidation with the condition of double drainage. If the same clay layer is underlain by a hard rock then the time taken to attain 50% consolidation is:a)100 daysb)800 daysc)1600 daysd)200 daysCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A clay layer 10 m thick in the field takes 400 days to attain 50% consolidation with the condition of double drainage. If the same clay layer is underlain by a hard rock then the time taken to attain 50% consolidation is:a)100 daysb)800 daysc)1600 daysd)200 daysCorrect answer is option 'C'. Can you explain this answer?.
Solutions for A clay layer 10 m thick in the field takes 400 days to attain 50% consolidation with the condition of double drainage. If the same clay layer is underlain by a hard rock then the time taken to attain 50% consolidation is:a)100 daysb)800 daysc)1600 daysd)200 daysCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of A clay layer 10 m thick in the field takes 400 days to attain 50% consolidation with the condition of double drainage. If the same clay layer is underlain by a hard rock then the time taken to attain 50% consolidation is:a)100 daysb)800 daysc)1600 daysd)200 daysCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A clay layer 10 m thick in the field takes 400 days to attain 50% consolidation with the condition of double drainage. If the same clay layer is underlain by a hard rock then the time taken to attain 50% consolidation is:a)100 daysb)800 daysc)1600 daysd)200 daysCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for A clay layer 10 m thick in the field takes 400 days to attain 50% consolidation with the condition of double drainage. If the same clay layer is underlain by a hard rock then the time taken to attain 50% consolidation is:a)100 daysb)800 daysc)1600 daysd)200 daysCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of A clay layer 10 m thick in the field takes 400 days to attain 50% consolidation with the condition of double drainage. If the same clay layer is underlain by a hard rock then the time taken to attain 50% consolidation is:a)100 daysb)800 daysc)1600 daysd)200 daysCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A clay layer 10 m thick in the field takes 400 days to attain 50% consolidation with the condition of double drainage. If the same clay layer is underlain by a hard rock then the time taken to attain 50% consolidation is:a)100 daysb)800 daysc)1600 daysd)200 daysCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.
|
|
Explore Courses for Civil Engineering (CE) exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup