DSSSB TGT/PGT/PRT Exam > DSSSB TGT/PGT/PRT Questions > Let P(n) be a statement and let P(n) ⇒ P...
Start Learning for Free
Let P(n) be a statement and let P(n) ⇒ P (n + 1) for all natural numbers n. Then, P(n) is true
- a)for all n
- b)for all n > 1
- c)for all n > m being a fixed positive integer
- d)Nothing can be said
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
Let P(n) be a statement and let P(n) ⇒ P (n + 1) for all natural ...
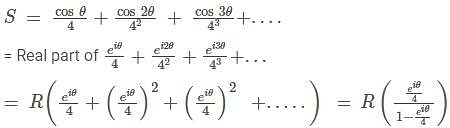
Sum of infinite terms of G.P.
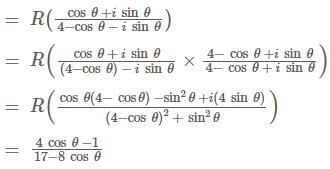

|
Explore Courses for DSSSB TGT/PGT/PRT exam
|

|
Similar DSSSB TGT/PGT/PRT Doubts
Let P(n) be a statement and let P(n) ⇒ P (n + 1) for all natural numbers n. Then, P(n) is truea)for all nb)for all n > 1c)for all n > m being a fixed positive integerd)Nothing can be saidCorrect answer is option 'D'. Can you explain this answer?
Question Description
Let P(n) be a statement and let P(n) ⇒ P (n + 1) for all natural numbers n. Then, P(n) is truea)for all nb)for all n > 1c)for all n > m being a fixed positive integerd)Nothing can be saidCorrect answer is option 'D'. Can you explain this answer? for DSSSB TGT/PGT/PRT 2025 is part of DSSSB TGT/PGT/PRT preparation. The Question and answers have been prepared according to the DSSSB TGT/PGT/PRT exam syllabus. Information about Let P(n) be a statement and let P(n) ⇒ P (n + 1) for all natural numbers n. Then, P(n) is truea)for all nb)for all n > 1c)for all n > m being a fixed positive integerd)Nothing can be saidCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for DSSSB TGT/PGT/PRT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Let P(n) be a statement and let P(n) ⇒ P (n + 1) for all natural numbers n. Then, P(n) is truea)for all nb)for all n > 1c)for all n > m being a fixed positive integerd)Nothing can be saidCorrect answer is option 'D'. Can you explain this answer?.
Let P(n) be a statement and let P(n) ⇒ P (n + 1) for all natural numbers n. Then, P(n) is truea)for all nb)for all n > 1c)for all n > m being a fixed positive integerd)Nothing can be saidCorrect answer is option 'D'. Can you explain this answer? for DSSSB TGT/PGT/PRT 2025 is part of DSSSB TGT/PGT/PRT preparation. The Question and answers have been prepared according to the DSSSB TGT/PGT/PRT exam syllabus. Information about Let P(n) be a statement and let P(n) ⇒ P (n + 1) for all natural numbers n. Then, P(n) is truea)for all nb)for all n > 1c)for all n > m being a fixed positive integerd)Nothing can be saidCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for DSSSB TGT/PGT/PRT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Let P(n) be a statement and let P(n) ⇒ P (n + 1) for all natural numbers n. Then, P(n) is truea)for all nb)for all n > 1c)for all n > m being a fixed positive integerd)Nothing can be saidCorrect answer is option 'D'. Can you explain this answer?.
Solutions for Let P(n) be a statement and let P(n) ⇒ P (n + 1) for all natural numbers n. Then, P(n) is truea)for all nb)for all n > 1c)for all n > m being a fixed positive integerd)Nothing can be saidCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for DSSSB TGT/PGT/PRT.
Download more important topics, notes, lectures and mock test series for DSSSB TGT/PGT/PRT Exam by signing up for free.
Here you can find the meaning of Let P(n) be a statement and let P(n) ⇒ P (n + 1) for all natural numbers n. Then, P(n) is truea)for all nb)for all n > 1c)for all n > m being a fixed positive integerd)Nothing can be saidCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Let P(n) be a statement and let P(n) ⇒ P (n + 1) for all natural numbers n. Then, P(n) is truea)for all nb)for all n > 1c)for all n > m being a fixed positive integerd)Nothing can be saidCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for Let P(n) be a statement and let P(n) ⇒ P (n + 1) for all natural numbers n. Then, P(n) is truea)for all nb)for all n > 1c)for all n > m being a fixed positive integerd)Nothing can be saidCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of Let P(n) be a statement and let P(n) ⇒ P (n + 1) for all natural numbers n. Then, P(n) is truea)for all nb)for all n > 1c)for all n > m being a fixed positive integerd)Nothing can be saidCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Let P(n) be a statement and let P(n) ⇒ P (n + 1) for all natural numbers n. Then, P(n) is truea)for all nb)for all n > 1c)for all n > m being a fixed positive integerd)Nothing can be saidCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice DSSSB TGT/PGT/PRT tests.

|
Explore Courses for DSSSB TGT/PGT/PRT exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























