Class 11 Exam > Class 11 Questions > A U-tube having horizontal arm of length 20 c...
Start Learning for Free
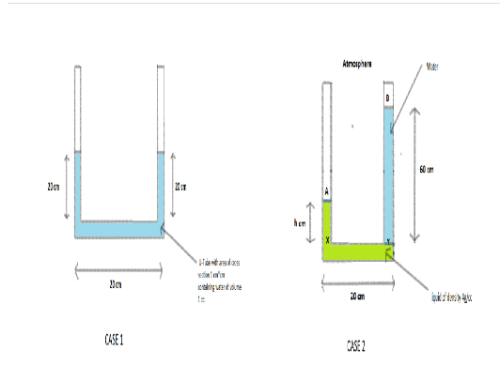
A U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area = 1 cm2. It is filled with water of volume 60 cc. What volume of a liquid of density 4 g/cc should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube?
- a)60 cc
- b)45 cc
- c)50 cc
- d)35 cc
Correct answer is option 'D'. Can you explain this answer?
Most Upvoted Answer
A U-tube having horizontal arm of length 20 cm, has uniform cross-sect...

Free Test
FREE
| Start Free Test |
Community Answer
A U-tube having horizontal arm of length 20 cm, has uniform cross-sect...
Given:
Length of horizontal arm of U-tube = 20 cm
Cross-sectional area = 1 cm^2
Volume of water initially present = 60 cc
Density of liquid to be poured = 4 g/cc
To find: Volume of liquid to be poured so that no water is left in the horizontal arm of the tube.
Solution:
Let the length of the vertical arms of the U-tube be h1 and h2. Let the height of the water column in the left arm be h and the height of the liquid column in the right arm be H.
Initial condition: Both arms are filled with water up to the same height h.
Volume of water in the left arm = A*h = 1*20*h = 20h cc
Volume of water in the right arm = A*H = 1*20*(h2-H) = 20h2-20H cc
Total volume of water = 20h + 20h2 - 20H
When a liquid of density 4 g/cc is poured into the right arm, it will exert a pressure on the water column in the left arm. Let the height of the water column in the left arm be h'. Then, the pressure exerted by the liquid column in the right arm on the water column in the left arm is given by:
P = ρgh' = 4*10*h' dyn/cm^2
Where g=10 m/s^2 is the acceleration due to gravity.
Since the U-tube is in equilibrium, the pressure difference between the two arms must be zero. Hence,
ρwgh = ρlgh'
where ρw = 1 g/cc is the density of water.
Solving for h', we get:
h' = h(ρw/ρl) = h/4
Now, the volume of liquid poured into the right arm is given by:
Volume of liquid = A*(h2-H) - A*h' = 20(h2-H) - 5h
We need to find the volume of liquid poured such that there is no water left in the horizontal arm. This means that the height of the water column in the left arm becomes zero, i.e., h' = 0. Substituting h' = 0 in the above equation, we get:
20(h2-H) - 5h = 0
Solving for H, we get:
H = (4h)/20 = h/5
Substituting this value of H in the equation for the volume of liquid poured, we get:
Volume of liquid = 20(h2 - h/5) - 5h = 20h2 - 6h
Given that the volume of water initially present is 60 cc. Hence, 20h = 60 or h = 3 cm.
Substituting this value of h in the equation for the volume of liquid poured, we get:
Volume of liquid = 20h2 - 6h = 20(20-3) - 6(3) = 380 - 18 = 362 cc
Therefore, the volume of liquid to be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube is 35 cc (option D).
Length of horizontal arm of U-tube = 20 cm
Cross-sectional area = 1 cm^2
Volume of water initially present = 60 cc
Density of liquid to be poured = 4 g/cc
To find: Volume of liquid to be poured so that no water is left in the horizontal arm of the tube.
Solution:
Let the length of the vertical arms of the U-tube be h1 and h2. Let the height of the water column in the left arm be h and the height of the liquid column in the right arm be H.
Initial condition: Both arms are filled with water up to the same height h.
Volume of water in the left arm = A*h = 1*20*h = 20h cc
Volume of water in the right arm = A*H = 1*20*(h2-H) = 20h2-20H cc
Total volume of water = 20h + 20h2 - 20H
When a liquid of density 4 g/cc is poured into the right arm, it will exert a pressure on the water column in the left arm. Let the height of the water column in the left arm be h'. Then, the pressure exerted by the liquid column in the right arm on the water column in the left arm is given by:
P = ρgh' = 4*10*h' dyn/cm^2
Where g=10 m/s^2 is the acceleration due to gravity.
Since the U-tube is in equilibrium, the pressure difference between the two arms must be zero. Hence,
ρwgh = ρlgh'
where ρw = 1 g/cc is the density of water.
Solving for h', we get:
h' = h(ρw/ρl) = h/4
Now, the volume of liquid poured into the right arm is given by:
Volume of liquid = A*(h2-H) - A*h' = 20(h2-H) - 5h
We need to find the volume of liquid poured such that there is no water left in the horizontal arm. This means that the height of the water column in the left arm becomes zero, i.e., h' = 0. Substituting h' = 0 in the above equation, we get:
20(h2-H) - 5h = 0
Solving for H, we get:
H = (4h)/20 = h/5
Substituting this value of H in the equation for the volume of liquid poured, we get:
Volume of liquid = 20(h2 - h/5) - 5h = 20h2 - 6h
Given that the volume of water initially present is 60 cc. Hence, 20h = 60 or h = 3 cm.
Substituting this value of h in the equation for the volume of liquid poured, we get:
Volume of liquid = 20h2 - 6h = 20(20-3) - 6(3) = 380 - 18 = 362 cc
Therefore, the volume of liquid to be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube is 35 cc (option D).

|
Explore Courses for Class 11 exam
|

|
Question Description
A U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area = 1 cm2. It is filled with water of volume 60 cc. What volume of a liquid of density 4 g/cc should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube?a)60 ccb)45 ccc)50 ccd)35 ccCorrect answer is option 'D'. Can you explain this answer? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about A U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area = 1 cm2. It is filled with water of volume 60 cc. What volume of a liquid of density 4 g/cc should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube?a)60 ccb)45 ccc)50 ccd)35 ccCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area = 1 cm2. It is filled with water of volume 60 cc. What volume of a liquid of density 4 g/cc should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube?a)60 ccb)45 ccc)50 ccd)35 ccCorrect answer is option 'D'. Can you explain this answer?.
A U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area = 1 cm2. It is filled with water of volume 60 cc. What volume of a liquid of density 4 g/cc should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube?a)60 ccb)45 ccc)50 ccd)35 ccCorrect answer is option 'D'. Can you explain this answer? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about A U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area = 1 cm2. It is filled with water of volume 60 cc. What volume of a liquid of density 4 g/cc should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube?a)60 ccb)45 ccc)50 ccd)35 ccCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area = 1 cm2. It is filled with water of volume 60 cc. What volume of a liquid of density 4 g/cc should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube?a)60 ccb)45 ccc)50 ccd)35 ccCorrect answer is option 'D'. Can you explain this answer?.
Solutions for A U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area = 1 cm2. It is filled with water of volume 60 cc. What volume of a liquid of density 4 g/cc should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube?a)60 ccb)45 ccc)50 ccd)35 ccCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of A U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area = 1 cm2. It is filled with water of volume 60 cc. What volume of a liquid of density 4 g/cc should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube?a)60 ccb)45 ccc)50 ccd)35 ccCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area = 1 cm2. It is filled with water of volume 60 cc. What volume of a liquid of density 4 g/cc should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube?a)60 ccb)45 ccc)50 ccd)35 ccCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for A U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area = 1 cm2. It is filled with water of volume 60 cc. What volume of a liquid of density 4 g/cc should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube?a)60 ccb)45 ccc)50 ccd)35 ccCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of A U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area = 1 cm2. It is filled with water of volume 60 cc. What volume of a liquid of density 4 g/cc should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube?a)60 ccb)45 ccc)50 ccd)35 ccCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area = 1 cm2. It is filled with water of volume 60 cc. What volume of a liquid of density 4 g/cc should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube?a)60 ccb)45 ccc)50 ccd)35 ccCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Class 11 tests.

|
Explore Courses for Class 11 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























