Class 10 Exam > Class 10 Questions > A student is not able to see distinctly the o...
Start Learning for Free
A student is not able to see distinctly the objects placed beyond 5 m. State the name of the defect the student is suffering from and list 2 possible reasons for the defect. How can it be corrected? Find the power of his corrective lens.?
Most Upvoted Answer
A student is not able to see distinctly the objects placed beyond 5 m....
There are some possible reason due to this defect of vision may have arisen :
(a) elongation of eyeball
(b) excessive curvature of the lens.
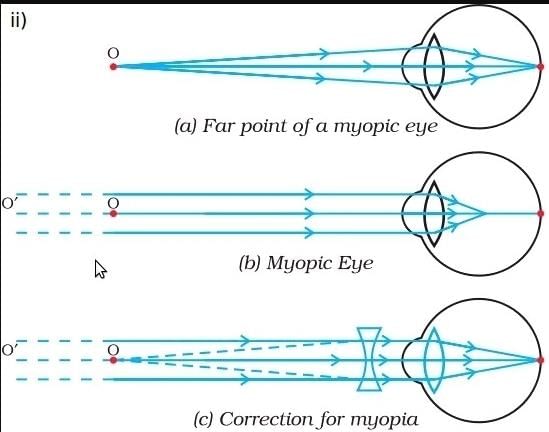
(i) student unable to see distinctly the objects placed beyond 5m from his eyes because student suffering with myopia . A myopic eye can't see distinct object clearly but able to see nearby object clearly.
(ii) convex lens of suitable focal length is used to restore proper vision. After using convex , image formed at ratina. While before it , image was formed near the ratina . As shown in figure it is clear how the lens correct this type of defect.
b. Focal length of convex lens is positive
So, f = +5m
Now, Power = 1/f = +1/5 = +0.2D
Hence, power is +0.2 diopter
Community Answer
A student is not able to see distinctly the objects placed beyond 5 m....
The Defect:
The student is suffering from myopia, also known as nearsightedness. In this condition, the person is unable to see distant objects clearly while having a normal or relatively good vision for close objects.
Possible Reasons for the Defect:
There are two possible reasons for the student's myopia:
1. Elongated Eyeball: In a normal eye, light rays entering the eye converge at the retina, resulting in clear vision. However, in myopia, the eyeball is elongated, causing the light rays to converge in front of the retina instead of directly on it. As a result, the images formed on the retina are blurred, leading to difficulty in seeing distant objects clearly.
2. Increased Curvature of the Cornea: Another possible reason for myopia is an increased curvature of the cornea. This altered shape of the cornea causes light rays to bend more sharply, again resulting in the formation of an image in front of the retina.
Correction:
Myopia can be corrected using concave lenses. These lenses are thinner at the center and thicker at the edges, causing the light rays to diverge before entering the eye. This divergence of light compensates for the excessive convergence caused by the elongated eyeball or increased corneal curvature, allowing the light rays to focus directly on the retina.
Power of the Corrective Lens:
The power of the corrective lens required to correct myopia can be determined by the degree of nearsightedness. The power of the lens is measured in units called diopters (D), which indicate the focusing ability of the lens.
To calculate the power of the corrective lens, the reciprocal of the farthest point at which the student can see clearly is taken. In this case, the student is unable to see distinctly beyond 5 meters. Therefore, the power of the corrective lens can be calculated as follows:
Power of the lens = 1 / Farthest point of clear vision
= 1 / 5 meters
= 0.2 D
Therefore, the power of the corrective lens required for the student to see distant objects clearly is 0.2 diopters.

|
Explore Courses for Class 10 exam
|

|
Similar Class 10 Doubts
Question Description
A student is not able to see distinctly the objects placed beyond 5 m. State the name of the defect the student is suffering from and list 2 possible reasons for the defect. How can it be corrected? Find the power of his corrective lens.? for Class 10 2025 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about A student is not able to see distinctly the objects placed beyond 5 m. State the name of the defect the student is suffering from and list 2 possible reasons for the defect. How can it be corrected? Find the power of his corrective lens.? covers all topics & solutions for Class 10 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A student is not able to see distinctly the objects placed beyond 5 m. State the name of the defect the student is suffering from and list 2 possible reasons for the defect. How can it be corrected? Find the power of his corrective lens.?.
A student is not able to see distinctly the objects placed beyond 5 m. State the name of the defect the student is suffering from and list 2 possible reasons for the defect. How can it be corrected? Find the power of his corrective lens.? for Class 10 2025 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about A student is not able to see distinctly the objects placed beyond 5 m. State the name of the defect the student is suffering from and list 2 possible reasons for the defect. How can it be corrected? Find the power of his corrective lens.? covers all topics & solutions for Class 10 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A student is not able to see distinctly the objects placed beyond 5 m. State the name of the defect the student is suffering from and list 2 possible reasons for the defect. How can it be corrected? Find the power of his corrective lens.?.
Solutions for A student is not able to see distinctly the objects placed beyond 5 m. State the name of the defect the student is suffering from and list 2 possible reasons for the defect. How can it be corrected? Find the power of his corrective lens.? in English & in Hindi are available as part of our courses for Class 10.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Here you can find the meaning of A student is not able to see distinctly the objects placed beyond 5 m. State the name of the defect the student is suffering from and list 2 possible reasons for the defect. How can it be corrected? Find the power of his corrective lens.? defined & explained in the simplest way possible. Besides giving the explanation of
A student is not able to see distinctly the objects placed beyond 5 m. State the name of the defect the student is suffering from and list 2 possible reasons for the defect. How can it be corrected? Find the power of his corrective lens.?, a detailed solution for A student is not able to see distinctly the objects placed beyond 5 m. State the name of the defect the student is suffering from and list 2 possible reasons for the defect. How can it be corrected? Find the power of his corrective lens.? has been provided alongside types of A student is not able to see distinctly the objects placed beyond 5 m. State the name of the defect the student is suffering from and list 2 possible reasons for the defect. How can it be corrected? Find the power of his corrective lens.? theory, EduRev gives you an
ample number of questions to practice A student is not able to see distinctly the objects placed beyond 5 m. State the name of the defect the student is suffering from and list 2 possible reasons for the defect. How can it be corrected? Find the power of his corrective lens.? tests, examples and also practice Class 10 tests.

|
Explore Courses for Class 10 exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



























