Class 9 Exam > Class 9 Questions > A cylinderical vessel contains 49.896 litres ...
Start Learning for Free
A cylinderical vessel contains 49.896 litres of liquid. cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.
Then its total surface area is ______.
- a)5724 cm2
- b)7524 cm2
- c)5742 cm2
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A cylinderical vessel contains 49.896 litres of liquid. cost of painti...

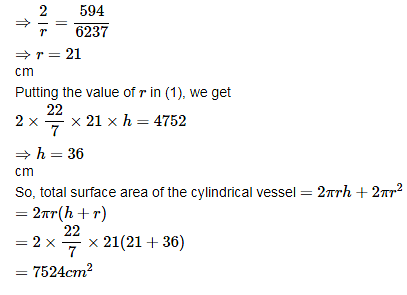
Most Upvoted Answer
A cylinderical vessel contains 49.896 litres of liquid. cost of painti...
Question:
Find the total surface area of a cylindrical vessel that contains 49.896 litres of liquid and the cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.
Solution:
Let the radius of the cylindrical vessel be r and the height be h.
Volume of the cylindrical vessel = πr²h = 49.896 litres = 49896 cm³
Now, we know that the cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.
Let the total surface area of the cylindrical vessel be A.
Cost of painting = 2paise/sq cm = Rs. 0.02/sq cm
Cost of painting the entire surface area = Rs. 95.04
Therefore, we have:
Rs. 0.02/sq cm x A = Rs. 95.04
A = 95.04/0.02 = 4752 sq cm
Now, the total surface area of the cylindrical vessel is given by:
Total surface area = 2πrh + 2πr²
We can solve for h using the volume of the cylindrical vessel:
πr²h = 49896
h = 49896/πr²
Substituting this value of h in the expression for total surface area, we get:
Total surface area = 2πr(49896/πr²) + 2πr²
Total surface area = 2(49896/r) + 2πr²
To find the value of r that minimizes the surface area, we differentiate the expression for surface area with respect to r:
d/dx(2(49896/r) + 2πr²) = -99896/r² + 4πr
Setting this derivative equal to zero, we get:
-99896/r² + 4πr = 0
r³ = 99896/4π
r = 14.04 cm (approx.)
Substituting this value of r in the expression for total surface area, we get:
Total surface area = 2π(14.04)(49896/π(14.04)²) + 2π(14.04)²
Total surface area = 7524 cm²
Therefore, the total surface area of the cylindrical vessel is 7524 cm².
Find the total surface area of a cylindrical vessel that contains 49.896 litres of liquid and the cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.
Solution:
Let the radius of the cylindrical vessel be r and the height be h.
Volume of the cylindrical vessel = πr²h = 49.896 litres = 49896 cm³
Now, we know that the cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.
Let the total surface area of the cylindrical vessel be A.
Cost of painting = 2paise/sq cm = Rs. 0.02/sq cm
Cost of painting the entire surface area = Rs. 95.04
Therefore, we have:
Rs. 0.02/sq cm x A = Rs. 95.04
A = 95.04/0.02 = 4752 sq cm
Now, the total surface area of the cylindrical vessel is given by:
Total surface area = 2πrh + 2πr²
We can solve for h using the volume of the cylindrical vessel:
πr²h = 49896
h = 49896/πr²
Substituting this value of h in the expression for total surface area, we get:
Total surface area = 2πr(49896/πr²) + 2πr²
Total surface area = 2(49896/r) + 2πr²
To find the value of r that minimizes the surface area, we differentiate the expression for surface area with respect to r:
d/dx(2(49896/r) + 2πr²) = -99896/r² + 4πr
Setting this derivative equal to zero, we get:
-99896/r² + 4πr = 0
r³ = 99896/4π
r = 14.04 cm (approx.)
Substituting this value of r in the expression for total surface area, we get:
Total surface area = 2π(14.04)(49896/π(14.04)²) + 2π(14.04)²
Total surface area = 7524 cm²
Therefore, the total surface area of the cylindrical vessel is 7524 cm².
Free Test
FREE
| Start Free Test |
Community Answer
A cylinderical vessel contains 49.896 litres of liquid. cost of painti...
Genius
GIVEN:
Volume of cylindrical vessel= 49.896 L
= 49.896× 1000 = 49896 cm³
[ 1 L = 1000 cm³]
Cost of painting at 2 paise per square cm= ₹ 95.04
Curved surface area of cylinder= cost / rate
Curved surface area of cylinder=95.04/.02
Curved surface area of cylinder= 4752 cm²
Let r and h be the radius and height of the cylinder .
Curved surface area of cylinder= 2πrh
2πrh = 4752……..(1)
Volume of Cylinder= πr²h
πr²h= 49896 ……….(2)
From equation 1 and 2
2πrh/πr²h = 4752/49896
2/r = 594/6237
r= 21 cm
Put this value of r in eq 1
2πrh = 4752
2 × (22/7)× 21× h= 4752
2×22×3×h = 4752
h= 4752/2×22×3
h= 36 cm
Total surface area of the cylindrical vessel= 2πr(h+r)
= 2×(22/7)×21(21+36)
= 2×22×3(57)
= 7524 cm²
Hence, the total surface area of the cylindrical vessel is 7524 cm²
Hope this will help you....
GIVEN:
Volume of cylindrical vessel= 49.896 L
= 49.896× 1000 = 49896 cm³
[ 1 L = 1000 cm³]
Cost of painting at 2 paise per square cm= ₹ 95.04
Curved surface area of cylinder= cost / rate
Curved surface area of cylinder=95.04/.02
Curved surface area of cylinder= 4752 cm²
Let r and h be the radius and height of the cylinder .
Curved surface area of cylinder= 2πrh
2πrh = 4752……..(1)
Volume of Cylinder= πr²h
πr²h= 49896 ……….(2)
From equation 1 and 2
2πrh/πr²h = 4752/49896
2/r = 594/6237
r= 21 cm
Put this value of r in eq 1
2πrh = 4752
2 × (22/7)× 21× h= 4752
2×22×3×h = 4752
h= 4752/2×22×3
h= 36 cm
Total surface area of the cylindrical vessel= 2πr(h+r)
= 2×(22/7)×21(21+36)
= 2×22×3(57)
= 7524 cm²
Hence, the total surface area of the cylindrical vessel is 7524 cm²
Hope this will help you....
Attention Class 9 Students!
To make sure you are not studying endlessly, EduRev has designed Class 9 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 9.

|
Explore Courses for Class 9 exam
|

|
A cylinderical vessel contains 49.896 litres of liquid. cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.Then its total surface area is ______.a)5724 cm2b)7524cm2c)5742cm2d)None of theseCorrect answer is option 'B'. Can you explain this answer?
Question Description
A cylinderical vessel contains 49.896 litres of liquid. cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.Then its total surface area is ______.a)5724 cm2b)7524cm2c)5742cm2d)None of theseCorrect answer is option 'B'. Can you explain this answer? for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about A cylinderical vessel contains 49.896 litres of liquid. cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.Then its total surface area is ______.a)5724 cm2b)7524cm2c)5742cm2d)None of theseCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A cylinderical vessel contains 49.896 litres of liquid. cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.Then its total surface area is ______.a)5724 cm2b)7524cm2c)5742cm2d)None of theseCorrect answer is option 'B'. Can you explain this answer?.
A cylinderical vessel contains 49.896 litres of liquid. cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.Then its total surface area is ______.a)5724 cm2b)7524cm2c)5742cm2d)None of theseCorrect answer is option 'B'. Can you explain this answer? for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about A cylinderical vessel contains 49.896 litres of liquid. cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.Then its total surface area is ______.a)5724 cm2b)7524cm2c)5742cm2d)None of theseCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A cylinderical vessel contains 49.896 litres of liquid. cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.Then its total surface area is ______.a)5724 cm2b)7524cm2c)5742cm2d)None of theseCorrect answer is option 'B'. Can you explain this answer?.
Solutions for A cylinderical vessel contains 49.896 litres of liquid. cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.Then its total surface area is ______.a)5724 cm2b)7524cm2c)5742cm2d)None of theseCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of A cylinderical vessel contains 49.896 litres of liquid. cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.Then its total surface area is ______.a)5724 cm2b)7524cm2c)5742cm2d)None of theseCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A cylinderical vessel contains 49.896 litres of liquid. cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.Then its total surface area is ______.a)5724 cm2b)7524cm2c)5742cm2d)None of theseCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for A cylinderical vessel contains 49.896 litres of liquid. cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.Then its total surface area is ______.a)5724 cm2b)7524cm2c)5742cm2d)None of theseCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of A cylinderical vessel contains 49.896 litres of liquid. cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.Then its total surface area is ______.a)5724 cm2b)7524cm2c)5742cm2d)None of theseCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A cylinderical vessel contains 49.896 litres of liquid. cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.Then its total surface area is ______.a)5724 cm2b)7524cm2c)5742cm2d)None of theseCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice Class 9 tests.

|
Explore Courses for Class 9 exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























