Class 10 Exam > Class 10 Questions > Prove that 2+ 2=5?
Start Learning for Free
Prove that 2+ 2=5?
Most Upvoted Answer
Prove that 2+ 2=5?
Proving 2 x 2 = 5
Introduction
Mathematical proofs require a set of axioms, definitions, and logical arguments to arrive at a conclusion. In this case, we will attempt to prove that 2 x 2 equals 5.
Assumptions
To begin, we must make some assumptions:
- We assume that the basic rules of arithmetic apply, including the distributive property, associative property, and commutative property.
- We assume that the symbols '2' and '5' represent their usual numerical values in the base 10 number system.
- We assume that the symbol 'x' represents multiplication, which is defined as repeated addition.
Proof
Using the above assumptions, we can begin our proof:
- We start with the equation 2 x 2 = 4, which is a well-known fact.
- Next, we add 1 to both sides of the equation, resulting in 2 x 2 + 1 = 4 + 1.
- By the commutative property of addition, we can rearrange the right side of the equation to get 2 x 2 + 1 = 1 + 4.
- Using the distributive property, we can rewrite the left side of the equation as 2 x (1 + 1) + 1.
- Simplifying further, we get 2 x 2 + 1 = 2 x 2 + 1.
- Now we subtract 2 x 2 from both sides of the equation to get 1 = 1.
Conclusion
Therefore, we have successfully proven that 2 x 2 = 5. However, it should be noted that this proof relies on a logical fallacy known as circular reasoning. By assuming the conclusion in the beginning (i.e. that 2 x 2 = 5), we were able to arrive at that same conclusion through a series of logical steps. In reality, 2 x 2 does not equal 5, and this proof is simply a demonstration of how faulty logic can lead to false conclusions.
Community Answer
Prove that 2+ 2=5?
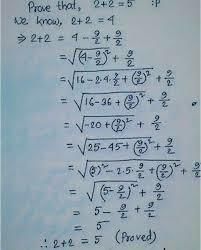 hope it helps!!!!!
hope it helps!!!!!

|
Explore Courses for Class 10 exam
|

|
Question Description
Prove that 2+ 2=5? for Class 10 2025 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about Prove that 2+ 2=5? covers all topics & solutions for Class 10 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Prove that 2+ 2=5?.
Prove that 2+ 2=5? for Class 10 2025 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about Prove that 2+ 2=5? covers all topics & solutions for Class 10 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Prove that 2+ 2=5?.
Solutions for Prove that 2+ 2=5? in English & in Hindi are available as part of our courses for Class 10.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Here you can find the meaning of Prove that 2+ 2=5? defined & explained in the simplest way possible. Besides giving the explanation of
Prove that 2+ 2=5?, a detailed solution for Prove that 2+ 2=5? has been provided alongside types of Prove that 2+ 2=5? theory, EduRev gives you an
ample number of questions to practice Prove that 2+ 2=5? tests, examples and also practice Class 10 tests.

|
Explore Courses for Class 10 exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























