Chemistry Exam > Chemistry Questions > Aluminum metal has a density of 2.72g/cm3 and...
Start Learning for Free
Aluminum metal has a density of 2.72g/cm3 and crystallizes in lattice with an edge length of 404 pm. Which of the following alternative are correct:
- a)It forms a base centered cubic unit cell
- b)It forms a face centered cubic unit cell
- c)Its coordination number is 8
- d)its coordination number is 6
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Aluminum metal has a density of 2.72g/cm3 and crystallizes in lattice ...
Ans.
Method to Solve :
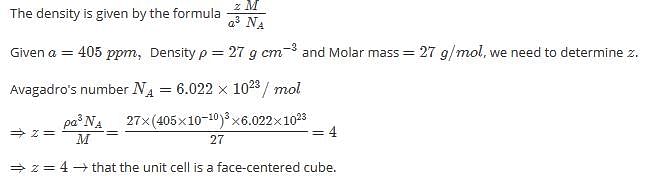
Most Upvoted Answer
Aluminum metal has a density of 2.72g/cm3 and crystallizes in lattice ...
Answer:
The given information states that the density of aluminum metal is 2.72 g/cm3 and it crystallizes in a lattice with an edge length of 404 pm. We need to determine the type of unit cell formed by aluminum in its crystal lattice and its coordination number.
Unit Cell:
The density of a material is related to its molar mass and the volume of its unit cell. The molar mass of aluminum is 26.98 g/mol. To determine the volume of the unit cell, we can use the equation:
Density = (Molar Mass) / (Volume of Unit Cell)
2.72 g/cm3 = 26.98 g/mol / (Volume of Unit Cell)
Volume of Unit Cell = 26.98 g/mol / 2.72 g/cm3
The g units cancel out, and we are left with cm3 as the unit for volume. Dividing the values, we get:
Volume of Unit Cell = 9.92 cm3/mol
Face Centered Cubic (FCC) Unit Cell:
The volume of a face-centered cubic (FCC) unit cell can be calculated using the equation:
Volume of FCC Unit Cell = (4 * Al) / (Avogadro's Number)
where Al is the edge length of the unit cell and Avogadro's Number is approximately 6.022 × 10^23 mol-1.
Substituting the given value of Al = 404 pm = 4.04 Å into the equation, we get:
Volume of FCC Unit Cell = (4 * (4.04 Å)^3) / (6.022 × 10^23 mol-1)
Converting the Ångstrom (Å) unit to centimeters (cm), we have:
1 Å = 1 × 10^-8 cm
Therefore, the volume of the FCC unit cell in cm3 is:
Volume of FCC Unit Cell = (4 * (4.04 × 10^-8 cm)^3) / (6.022 × 10^23 mol-1)
Volume of FCC Unit Cell = 6.73 × 10^-24 cm3/mol
Comparing this with the calculated volume of the unit cell for aluminum, we can see that they are not equal. Therefore, aluminum does not form a face-centered cubic (FCC) unit cell.
Conclusion:
Based on the above analysis, we can conclude that the correct alternative is option 'B': Aluminum forms a face-centered cubic (FCC) unit cell.
Coordination Number:
The coordination number is the number of atoms or ions that surround a central atom or ion in a crystal lattice. In an FCC unit cell, each corner atom is shared by eight unit cells, and each face-centered atom is shared by two unit cells. Therefore, the coordination number for an FCC lattice is 12.
Since aluminum forms an FCC unit cell, the coordination number for aluminum is 12, which is not listed in the given options. Therefore, none of the provided options correctly state the coordination number for aluminum.
The given information states that the density of aluminum metal is 2.72 g/cm3 and it crystallizes in a lattice with an edge length of 404 pm. We need to determine the type of unit cell formed by aluminum in its crystal lattice and its coordination number.
Unit Cell:
The density of a material is related to its molar mass and the volume of its unit cell. The molar mass of aluminum is 26.98 g/mol. To determine the volume of the unit cell, we can use the equation:
Density = (Molar Mass) / (Volume of Unit Cell)
2.72 g/cm3 = 26.98 g/mol / (Volume of Unit Cell)
Volume of Unit Cell = 26.98 g/mol / 2.72 g/cm3
The g units cancel out, and we are left with cm3 as the unit for volume. Dividing the values, we get:
Volume of Unit Cell = 9.92 cm3/mol
Face Centered Cubic (FCC) Unit Cell:
The volume of a face-centered cubic (FCC) unit cell can be calculated using the equation:
Volume of FCC Unit Cell = (4 * Al) / (Avogadro's Number)
where Al is the edge length of the unit cell and Avogadro's Number is approximately 6.022 × 10^23 mol-1.
Substituting the given value of Al = 404 pm = 4.04 Å into the equation, we get:
Volume of FCC Unit Cell = (4 * (4.04 Å)^3) / (6.022 × 10^23 mol-1)
Converting the Ångstrom (Å) unit to centimeters (cm), we have:
1 Å = 1 × 10^-8 cm
Therefore, the volume of the FCC unit cell in cm3 is:
Volume of FCC Unit Cell = (4 * (4.04 × 10^-8 cm)^3) / (6.022 × 10^23 mol-1)
Volume of FCC Unit Cell = 6.73 × 10^-24 cm3/mol
Comparing this with the calculated volume of the unit cell for aluminum, we can see that they are not equal. Therefore, aluminum does not form a face-centered cubic (FCC) unit cell.
Conclusion:
Based on the above analysis, we can conclude that the correct alternative is option 'B': Aluminum forms a face-centered cubic (FCC) unit cell.
Coordination Number:
The coordination number is the number of atoms or ions that surround a central atom or ion in a crystal lattice. In an FCC unit cell, each corner atom is shared by eight unit cells, and each face-centered atom is shared by two unit cells. Therefore, the coordination number for an FCC lattice is 12.
Since aluminum forms an FCC unit cell, the coordination number for aluminum is 12, which is not listed in the given options. Therefore, none of the provided options correctly state the coordination number for aluminum.

|
Explore Courses for Chemistry exam
|

|
Similar Chemistry Doubts
Aluminum metal has a density of 2.72g/cm3 and crystallizes in lattice with an edge length of 404 pm. Which of the following alternative are correct:a)It forms a base centered cubic unit cellb)It forms a face centered cubic unit cellc)Its coordination number is 8d)its coordination number is 6Correct answer is option 'B'. Can you explain this answer?
Question Description
Aluminum metal has a density of 2.72g/cm3 and crystallizes in lattice with an edge length of 404 pm. Which of the following alternative are correct:a)It forms a base centered cubic unit cellb)It forms a face centered cubic unit cellc)Its coordination number is 8d)its coordination number is 6Correct answer is option 'B'. Can you explain this answer? for Chemistry 2024 is part of Chemistry preparation. The Question and answers have been prepared according to the Chemistry exam syllabus. Information about Aluminum metal has a density of 2.72g/cm3 and crystallizes in lattice with an edge length of 404 pm. Which of the following alternative are correct:a)It forms a base centered cubic unit cellb)It forms a face centered cubic unit cellc)Its coordination number is 8d)its coordination number is 6Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Chemistry 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Aluminum metal has a density of 2.72g/cm3 and crystallizes in lattice with an edge length of 404 pm. Which of the following alternative are correct:a)It forms a base centered cubic unit cellb)It forms a face centered cubic unit cellc)Its coordination number is 8d)its coordination number is 6Correct answer is option 'B'. Can you explain this answer?.
Aluminum metal has a density of 2.72g/cm3 and crystallizes in lattice with an edge length of 404 pm. Which of the following alternative are correct:a)It forms a base centered cubic unit cellb)It forms a face centered cubic unit cellc)Its coordination number is 8d)its coordination number is 6Correct answer is option 'B'. Can you explain this answer? for Chemistry 2024 is part of Chemistry preparation. The Question and answers have been prepared according to the Chemistry exam syllabus. Information about Aluminum metal has a density of 2.72g/cm3 and crystallizes in lattice with an edge length of 404 pm. Which of the following alternative are correct:a)It forms a base centered cubic unit cellb)It forms a face centered cubic unit cellc)Its coordination number is 8d)its coordination number is 6Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Chemistry 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Aluminum metal has a density of 2.72g/cm3 and crystallizes in lattice with an edge length of 404 pm. Which of the following alternative are correct:a)It forms a base centered cubic unit cellb)It forms a face centered cubic unit cellc)Its coordination number is 8d)its coordination number is 6Correct answer is option 'B'. Can you explain this answer?.
Solutions for Aluminum metal has a density of 2.72g/cm3 and crystallizes in lattice with an edge length of 404 pm. Which of the following alternative are correct:a)It forms a base centered cubic unit cellb)It forms a face centered cubic unit cellc)Its coordination number is 8d)its coordination number is 6Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Chemistry.
Download more important topics, notes, lectures and mock test series for Chemistry Exam by signing up for free.
Here you can find the meaning of Aluminum metal has a density of 2.72g/cm3 and crystallizes in lattice with an edge length of 404 pm. Which of the following alternative are correct:a)It forms a base centered cubic unit cellb)It forms a face centered cubic unit cellc)Its coordination number is 8d)its coordination number is 6Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Aluminum metal has a density of 2.72g/cm3 and crystallizes in lattice with an edge length of 404 pm. Which of the following alternative are correct:a)It forms a base centered cubic unit cellb)It forms a face centered cubic unit cellc)Its coordination number is 8d)its coordination number is 6Correct answer is option 'B'. Can you explain this answer?, a detailed solution for Aluminum metal has a density of 2.72g/cm3 and crystallizes in lattice with an edge length of 404 pm. Which of the following alternative are correct:a)It forms a base centered cubic unit cellb)It forms a face centered cubic unit cellc)Its coordination number is 8d)its coordination number is 6Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of Aluminum metal has a density of 2.72g/cm3 and crystallizes in lattice with an edge length of 404 pm. Which of the following alternative are correct:a)It forms a base centered cubic unit cellb)It forms a face centered cubic unit cellc)Its coordination number is 8d)its coordination number is 6Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Aluminum metal has a density of 2.72g/cm3 and crystallizes in lattice with an edge length of 404 pm. Which of the following alternative are correct:a)It forms a base centered cubic unit cellb)It forms a face centered cubic unit cellc)Its coordination number is 8d)its coordination number is 6Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice Chemistry tests.

|
Explore Courses for Chemistry exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















