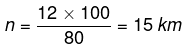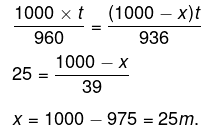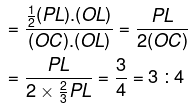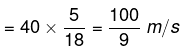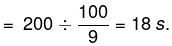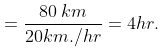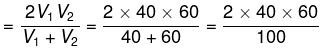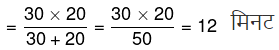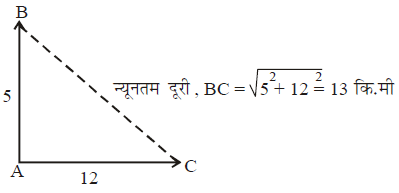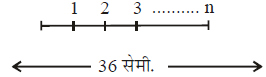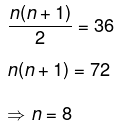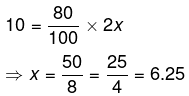प्रश्न.1. जब एक धाविका किसी दौड़ में 12 km दूरी दर्शाने वाले चिह्न को पार कर रही थी, तब उसे यह बताया गया कि उसने दौड़ का केवल 80% हिस्सा पूरा किया है। इस स्पर्ध में इस धाविका को कितने किलोमीटर दौड़ना था? (2019)
(क) 14
(ख) 15
(ग) 16
(घ) 16.5
उत्तर. (ख)
उपाय.
माना कि धवक n कि.मी. दौड़ता है
तो,


प्रश्न.2. एक हजार (1000) मीटर की एक दौड़ में X, Y और Z तीन प्रतियोगी हैं। मान लीजिए कि वे सभी विभिन्न एकसमान गतियों से दौड़ते हैं। Y, X से 40 m आगे से दौड़ना शुरू करता है और Z, X से 64 m आगे से दौड़ना शुरू करता है। यदि y और Z को 1000 m की एक दौड़ में प्रतिस्पर्ध करनी है, तो, Z , Y से कितने मीटर आगे से दौड़ना शुरू करेगा? (2019)
(क) 20
(ख) 25
(ग) 30
(घ) 35
उत्तर. (ख)
उपाय.
x, y को 40 m का शुरआत देता है।
x, z को 64 m का शुरआत देता है।
माना कि सभी t घंटे में दौड़ पूरा करते हैं।
तो

पुनः माना कि y, z को x m. का शुरुआत देता है,
तो

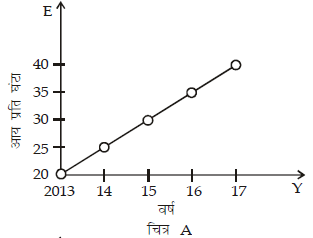
प्रश्न.3. चित्र A और B में एक फर्म में श्रमिकों की प्रति वर्ष औसत प्रति घंटा आय (E) निरूपित की गई हैः (2018)


चित्रों से यह देखा जा सकता है कि
(क) E के मूल्य अलग-अलग हैं
(ख) E के परिसर (अर्थात् अधिकतम एवं न्यूनतम के बीच का अंतर) अलग-अलग हैं
(ग) आलेखों (ग्राफ) की प्रवणता समान है
(घ) E में वृद्धि की दरें अलग-अलग हैं
उत्तर. (ग)
उपाय.
दिए गए ग्राफ के अनुसार दोनों ग्राफों की प्रवणता समान है।
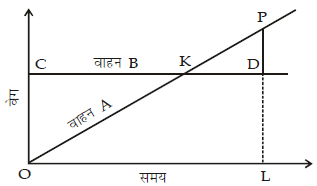
प्रश्न.4. नीचे दिए गए चित्रो में A और B दो वाहनों के वेग के आलेख (ग्राफ) दिए गए हैं। सरलरेखा OKP किसी भी क्षण में वाहन A के वेग को दर्शाती है, जबकि क्षैतिज सरलरेखा CKD किसी भी क्षण में वाहन B के वेग को दर्शाती है। चित्र में, D वह बिंदु है जहाँ P से क्षैतिज रेखा CKD पर लंब इस प्रकार मिलता है कि PD = 1/2LD

समय अंतराल OL में वाहन A और वाहन B द्वारा तय की गई दूरियों के बीच क्या अनुपात है? (2018)
(क) 1 : 2
(ख) 2 : 3
(ग) 3 : 4
(घ) 1 : 1
उत्तर. (ग)
उपाय.
आवश्यक अनुपात

प्रश्न.5. 200 मीटर लम्बी एक ट्रेन 40 किमी. प्रति घंटा की दर से चल रही है। रेलवे लाइन के निकट खड़े किसी व्यक्ति को यह ट्रेन कितने सेकंड में पार करेगी? (2018)
(क) 12
(ख) 15
(ग) 16
(घ) 18
उत्तर. (घ)
उपाय.
ट्रेन की लम्बाई = दूरी = 200 मी.
ट्रेन की चाल

आवश्यक समय

प्रश्न.6. दो व्यक्ति A और B किसी वृत्तीय मार्ग पर दौड़ रहे हैं। प्रारंभ में B,A से आगे है तथा उनकी स्थितियाँ वृत्त के केंद्र पर 30° का कोण बनाती हैं। जब A, उस बिंदु पर पहुँचता है जो कि उसके प्रारंभिक बिंदु से व्यासतः सम्मुख है, तब वह B से मिलता है। A और B की चालों मे क्या अनुपात है, यदि वे एकसमान चाल से दौड़ रहे हैं? (2018)
(क) 6 : 5
(ख) 4 : 3
(ग) 6 : 1
(घ) 4 : 2
उत्तर. (क)
उपाय.
B, A से 30° आगे है।
A द्वारा तय किया गया कुल कोण = 180°
B द्वारा तय किया गया कुल कोण = 180° - 30° = 150°
आवश्यक अनुपात = 180° : 150° = 6 : 5
प्रश्न.7. एक मालगाड़ी दिल्ली से मुंबई के लिए 40 km प्रति घंटे की औसत चाल से रवाना होती है। उसके दो घंटे पश्चात् एक एक्सप्रेस गाड़ी दिल्ली से मुंबई के लिए, पहले रवाना हुई मालगाड़ी के समांतर पथ पर, 60 km प्रति घंटे की औसत चाल से रवाना होती है। दिल्ली से कितनी दूरी पर एक्सप्रेस गाड़ी मालगाड़ी से मिलेगी? (2017)
(क) 480 km
(ख) 260 km
(ग) 240 km
(घ) 120 km
उत्तर. (ग)
उपाय.
2 घटें में मालगाडी द्वारा तय की गयी दूरी = 2×40 = 80 km
सापेक्ष गति = 60 km - 40 km = 20 km
इस प्रकार,
मालगाडी से मिलने के लिए एक्सप्रेस गाड़ी द्वारा लिया गया समय

इसलिए, तय की गयी दूरी = 4 × 60 = 240 Km.
प्रश्न.8. A और B पैदल चलते हुए एक वृत्ताकार पार्क का चक्कर लगाते हैं। वे दोनों प्रातः 8 बजे एक ही बिंदु से विपरीत दिशाओं में चलना शुरू करते हैं। A और B की चाल क्रमश: 2 चक्कर प्रति घंटा व 3 चक्कर प्रति घंटा है। प्रातः 8 बजे के बाद तथा प्रातः 9.30 बजे से पूर्व वे कितनी बार एक-दूसरे के सामने से गुजरेंगे? (2016)
(क) 7
(ख) 6
(ग) 5
(घ) 8
उत्तर. (क)
उपाय.
यहाँ A और B विपरित दिशा में घूम रहे हैं इसलिए सापेक्ष गति = 2 + 3 = 5 चक्र / घंटे, इस प्रकार वे दोनों 5 बार प्रति घंटे एक दूसरे को पार करते हैं और आधे घंटे में 2 बार अतः, एक दूसरे को 7 बार सुबह 9.30 बजे से पहले पार करते हैं।
प्रश्न.9. चार मित्रों A, B, C और D को एक पुल को पार करना है। पुल को एक समय में अधिक से अधिक दो व्यक्ति पार कर सकते हैं रात का समय हैं तथा उनके पास केवल एक लालटेन है। पुल पार करने वालों को रास्ता ढूँढ़ने के लिए लालटेन ले लेनी चाहिए। एक समय चलने वाले दो व्यक्तियों की धीमें चलने वाले व्यक्ति की चाल से चलना होगा। पुल पार करने के बाद दो व्यक्तियों में से ज्यादा तेज चलने वाला व्यक्ति, प्रत्येक बार अपने साथी को पुल पार करवा कर, लालटेन सहित वापस लौट आएगा। अंत में लालटेन को अपने मूल स्थान पर रखना है तथा लालटेन वापस रखने वाले व्यक्ति को लालटेन के बगैर पुल पार करना है। पुल पार करने के लिए उनके द्वारा लिया गया समय इस प्रकार है। (2016)
(A) 1 मिनट
(B) 2 मिनट
(C) 7 मिनट
(D) 10 मिनट। चारों मित्रों द्वारा पुल पार करने के लिए कुल कितना न्यूनतम समय आवश्यक है?
(क) 23 मिनट
(ख) 22 मिनट
(ग) 21 मिनट
(घ) 20 मिनट
उत्तर. (क)
उपाय.
यहाँ A को कम से कम समय लगता करने में अर्थात् 1 मिनट, D को 10 मिनट, C को 7 मिनट और B को 2 मिनट लेता पुल पार करने में, इस तरह, 4 दोस्त न्यूनतम समय में पुल पार करते हैं
1. A + B पार कर रहे हैं और A लौट रहा है, (2 + 1) मिनट
2. A + C पार कर रहे हैं और A लौट रहा है, (7 + 1) मिनट
3. A + D पार कर रहे हैं और A लौट रहा है, (10 + 1) मिनट
4. अंत समय में । पुल पार कर रहा हैः 1 मिनट अतः, कुल न्यूनतम समय = 3 + 8 + 11 + 1 = 23 मिनट
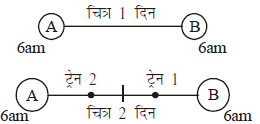
प्रश्न.10. स्टेशन A और स्टेशन B के बीच, प्रत्येक स्टेशन से 6 बजे सुबह चलने वाली दैनिक रेलगाड़ी आरंभ की जानी है और यह मात्र 42 घंटों में पूरी की जानी है। कितनी संख्या में रेलगाड़ियाँ चलानी होंगी जिससे कि प्रतिदिन सेवा जारी रहे? (2016)
(क) 2
(ख) 3
(ग) 4
(घ) 7
उत्तर. (ग)
उपाय.

उपर्युक्त चित्र दर्शाता है कि ट्रेन 1 स्टेशन A पहले दिन छोड़ी और ट्रेन 2 स्टेशन B 1 दिन छोड़ी दोनों ट्रेन 24 घंटे के बाद भी अपने गंतव्य तक नहीं पहुँच पाती जैसी कि यात्रा 42 घंटों पूरी की गई।
∴ दो ओर ट्रेनों को उस स्टेशन पर पेश किए जाने की जरूरत है
अर्थात् स्टेशन A और B, 4 ट्रेन अधिक प्रतिदिन सेवा को बनाए रखने के लिए आवश्यक है।
प्रश्न.11. 500 मीटर की दौड़ में, B, A से 45 मीटर आगे से प्रारम्भ करता है, लेकिन A दौड़ जीत जाता है जबकि B अभी भी 35 मीटर पीछे रहता है। यह मानते हएु कि दोनों एक ही समय दौड़ना प्रारम्भ करते हैं, A की चाल का B की चाल से, अनुपात क्या है ? (2015)
(क) 25 : 21
(ख) 25 : 20
(ग) 5 : 3
(घ) 5 : 7
उत्तर. (क)
उपाय.
कुल दूरी = 500 मी.
A के द्वारा तय की गई दूरी = 500 मी.
B के द्वारा तय की गई दूरी = 500 - 45 - 35 = 420

प्रश्न.12. दो शहर, A आरै B, एक-दसूरे से 360 किमी की दूरी पर हैं। एक कार A से B तक 40 किमी./घंटा. की चाल से जाती है और 60 किमी./घंटा की चाल से A तक लौट आती है। कार की औसत चाल क्या है? (2015)
(क) 45 किमी./घंटा
(ख) 48 किमी./घंटा
(ग) 50 किमी./घंटा
(घ) 55 किमी./घंटा
उत्तर. (ख)
उपाय.
दो कारों की औसत चाल जिसकी चाल V1आरै V2 किमी./घंटा

= 48 किमी./घंटा
प्रश्न.13. दो नल A और B किसी टंकी को क्रमशः 20 और 30 मिनट में पूरा भर सकते हैं। यदि दोनों नल एक साथ खोल दिए जाएं, तो टंकी को पूरी तरह भरने में उन्हें कितना समय लगेगा? (2015)
(क) 10 मिनट
(ख) 12 मिनट
(ग) 15 मिनट
(घ) 25 मिनट
उत्तर. (ख)
उपाय.
दोनों नलों द्वारा टंकी को पूरी तरह से भरने में लगा समय

प्रश्न.14. B की स्थिति A के उत्तर में है और C की स्थिति A के पूर्व में है। दूरियाँ AB और AC क्रमशः 5 कि.मी. और 12 कि.मी. है। B और C स्थानों के बीच की न्यूनतम दूरी (कि.मी. में.) क्या है ? (2014)
(क) 60
(ख) 13
(ग) 17
(घ) 7
उत्तर. (ख)
उपाय.

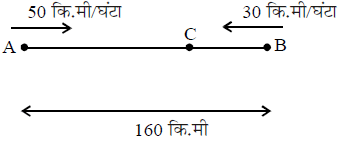
प्रश्न.15. 160 कि.मी. दूरी पर स्थित A और B दो स्थानों से दो कारें एक दूसरे की तरफ प्रस्थान करती है। दोनों कारें एक ही समय 08:10 पूर्वाह्न पर प्रस्थान करती हैं। यदि कारों की गति प्रति घंटे क्रमशः 50 कि.मी. और 30 कि.मी. है, तो कारें एक-दूसरे से किस समय पर मिलेंगी ? (2014)
(क) 10 : 10 पूर्वाह्न
(ख) 10 : 30 पूर्वाह्न
(ग) 11 : 10 पूर्वाह्न
(घ) 11 : 20 पूर्वाह्न
उत्तर. (क)
उपाय.

माना कि 't' घंटे के बाद कारें C बिन्दु पर मिलती हैं
∴ AC = 50 t तथा BC = 30 t
∴ 50 t + 30 t = 160
t = 160/80 = दो घंटे
अतः कारें 10 : 10 पूर्वाह्न पर मिलेगी।
प्रश्न.16.एक सरल रेखाखण्ड 36 से.मी. लंबा है। इस रेखा पर, रेखा के दोनों अंत्य बिन्दुओं से बिन्दु अंकित करने है। प्रत्येक अंत्य बिन्दु से, पहला बिन्दु अंत्य बिन्दु से 1 से.मी. की दूरी पर, दूसरा बिन्दु पहले बिन्दु से 2 सेमी. की दूरी पर तीसरा बिन्दु दूसरे बिन्दु से 3 से.मी. की दूरी पर है और यही क्रम आगे जारी है। यदि अंत्य बिन्दुओं को न गिना जाए और उभयनिष्ठ बिन्दुओं को 1 गिना जाए, तो बिन्दुओं की संख्या क्या है ? (2014)
(क) 10
(ख) 12
(ग) 14
(घ) 16
उत्तर. (ग)
उपाय.

∴ 1 + 2 + 3 + ........ n = 36

∴ अंतिम बिन्दु को छोड़कर, A से प्रारम्भ होने वाले बिन्दु 7 है। उसी प्रकार B से प्रारम्भ होकर, बिन्दुओं की संख्या 7 होगी। तथा A व B के बीच बिन्दुओं की संख्या समान होगी।
∴ सम्पूर्ण बिन्दुओं की संख्या = 7 + 7 = 14
प्रश्न.17. A और B बस द्वारा स्थान X से स्थान Y तक जाने का निश्चय करते हैं। A के पास ₹ 10 हैं और उसे पता चलता है कि यह राशि दो व्यक्तियों के लिए बस किराए का 80% है। B के पास ₹ 3 हैं, जिसे वह A को दे देता है। इस संदर्भ में, निम्नलिखित में से कौन-सा एक कथन सही है ? (2014)
(क) A के पास अब जो नकदी है, वह मात्र दो टिकटों के लिए ही पर्याप्त है।
(ख) A को टिकटें खरीदने के लिए ₹ 2 और चाहिए।
(ग) दो टिकट खरीदने के बाद A के पास 50 पैसे बच जाएंगे।
(घ) A के पास अब जो नकदी है, वह अभी भी दो टिकट खरीदने के लिए पर्याप्त नहीं है।
उत्तर. (ग)
उपाय.
माना 1 टिकट की कीमत = ₹ x
∴ A के लिए,

अब B, A को ₹ 3 देता है।
अतः A के पास ₹ 13 है।
2 टिकटों की कीमत = ₹ 12.50, जो दो टिकटें खरीदने से भी ज्यादा है।
∴ (a) नियम पर आधरित नहीं है।
(b) नियम पर स्पष्टः आधरित नहीं है।
(c) सही है, क्योंकि दो टिकट खरीदने के बाद A के पास बची हुई राशि = 13 - 12.50 = 50 पैसे।
प्रश्न.18. कोई श्रमिक अपने घर से फैक्टरी तक 5 किमी प्रति घंटा की गति से चलकर अपनी फैक्टरी में 3 मिनट विलंब से पहुंचता है। यदि वह 6 कि.मी. प्रति घंटा की गति से चलता है, तो वह फैक्टरी 7 मिनट पहले पहुंचता है। फैक्टरी से उसके घर की दूरी क्या है ? (2014)
(क) 3 कि.मी.
(ख) 4 कि.मी.
(ग) 5 कि.मी.
(घ) 6 कि.मी.
उत्तर. (ग)
उपाय.
माना दूरी = x km
प्रश्नानुसार,