Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > 3D Pythagoras & Trigonometry
3D Pythagoras & Trigonometry | Mathematics for GCSE/IGCSE - Class 10 PDF Download
3D Pythagoras & Trigonometry
What are Pythagoras & SOHCAHTOA?
- Pythagoras' Theorem helps us find missing side lengths of a right-angled triangle.
- It is also frequently used for finding the distance (or length) of a line.
- SOHCAHTOA is an acronym for the three trigonometric ratios that connect angles (θ) and sides (Opposite, Hypotenuse, and Adjacent) in a right-angled triangle.
- Sine – SOH – sin θ = Opposite ÷ Hypotenuse
- Cosine – CAH – cos θ = Adjacent ÷ Hypotenuse
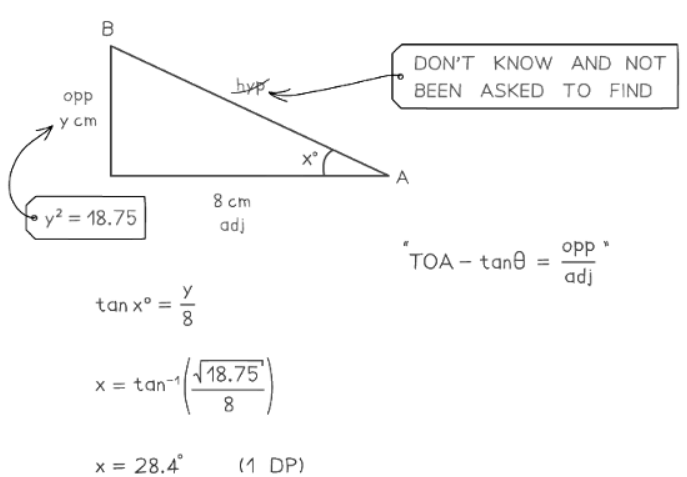
- Tangent – TOA – tan θ = Opposite ÷ Adjacent
How does Pythagoras work in 3D?
- 3D shapes can often be deconstructed into multiple 2D shapes, such as nets and surface areas.
- When applying Pythagoras' Theorem in 3D, focus on identifying right-angled triangles with two known sides and one unknown side.
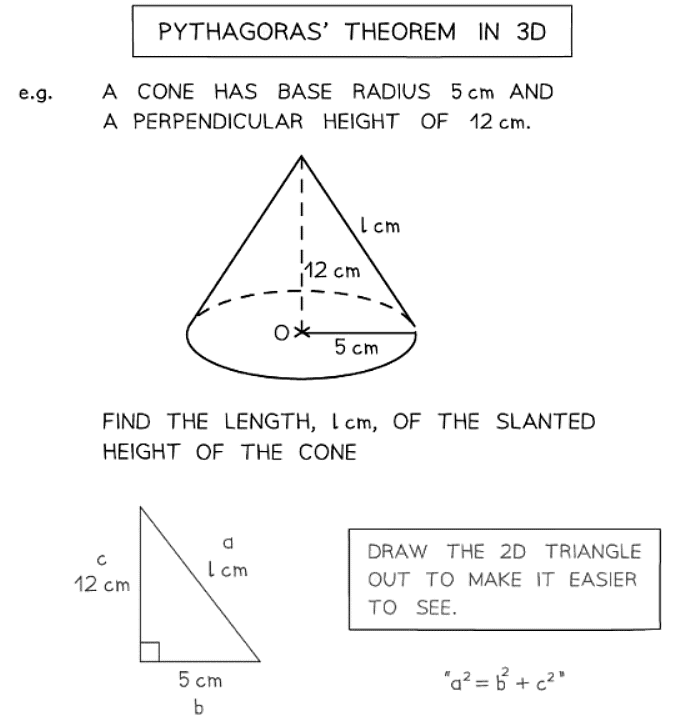
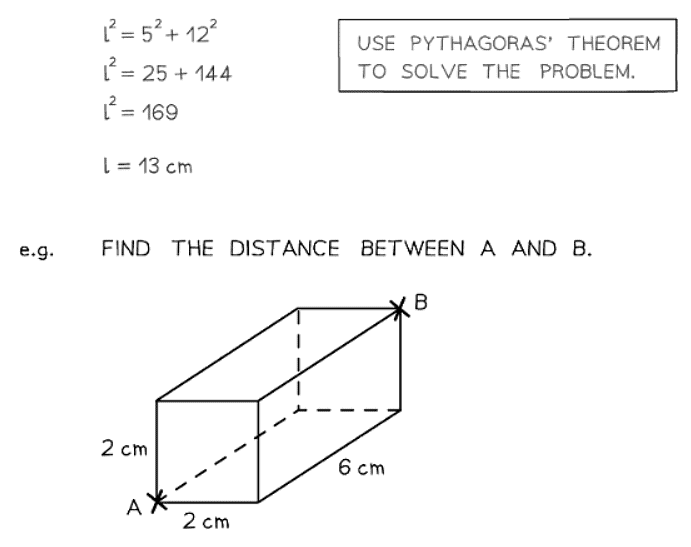
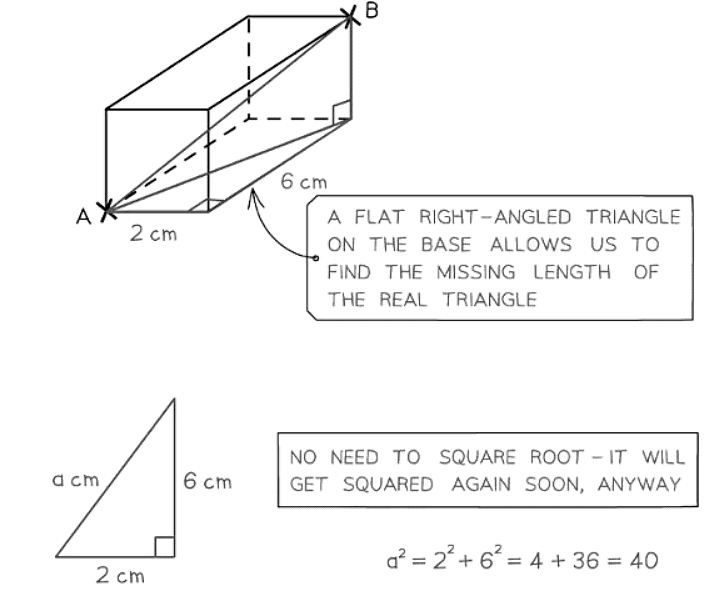
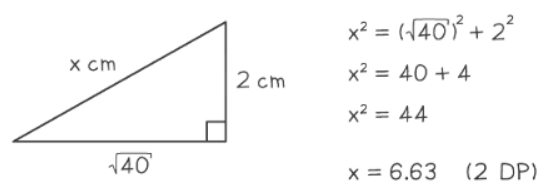
- The 3D version of the Pythagorean Theorem is expressed as d2 = x2 + y2 + z2.
- It is often simpler to solve 3D problems by breaking them into multiple 2D problems for better visualization.
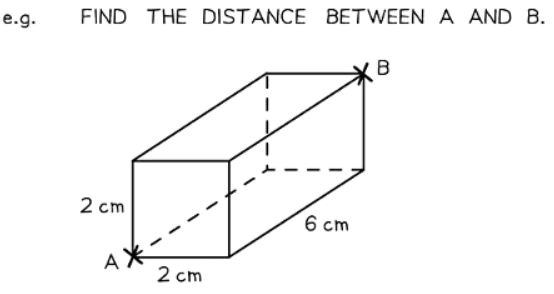
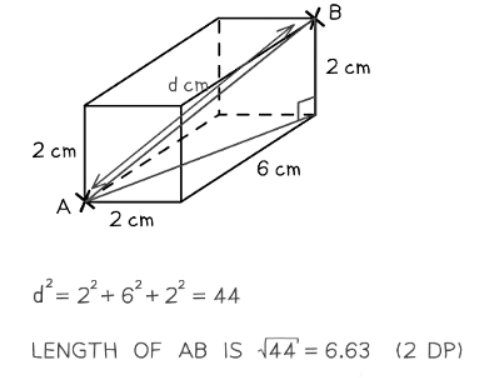
How does SOHCAHTOA work in 3D?
- Once more, seek out a combination of right-angled triangles that could help in determining the missing angle or side.
- In three-dimensional scenarios, the angle being dealt with might pose challenges.
- Determining the angle between a line and a plane is not always straightforward.
- If uncertainty arises, place a point on the line and extend a new line to the plane.
- This approach should establish a right-angled triangle, aiding in the solution process.
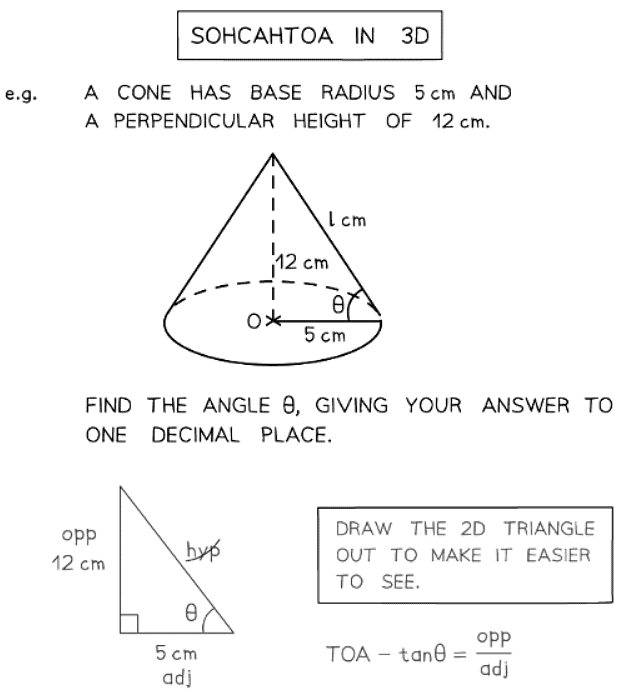
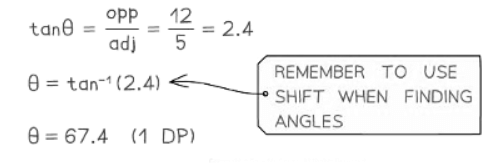
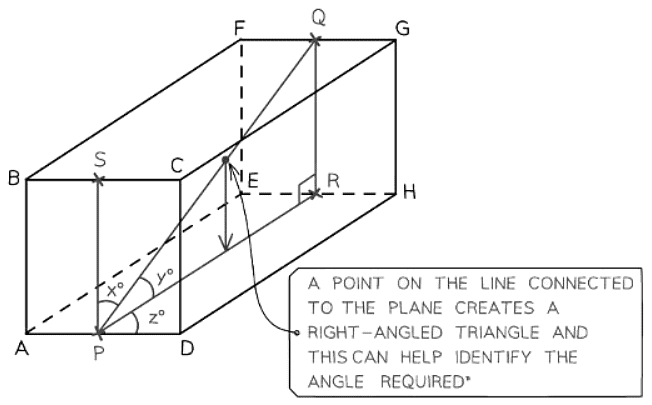

- Once you have your 2D triangle(s) you can begin to solve problems.
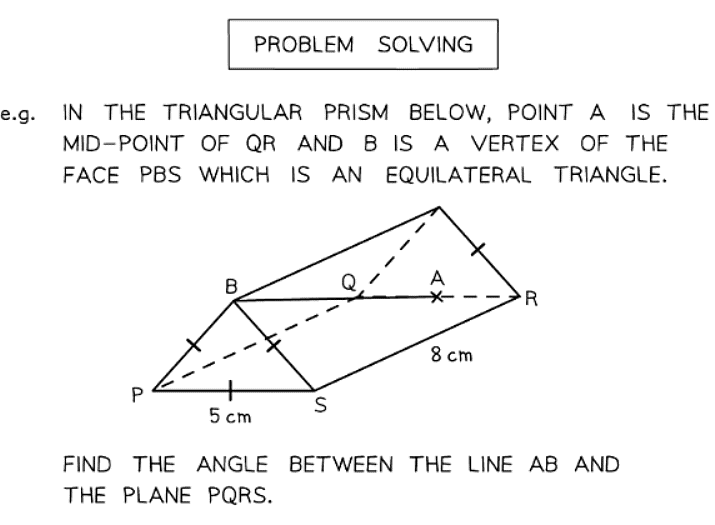
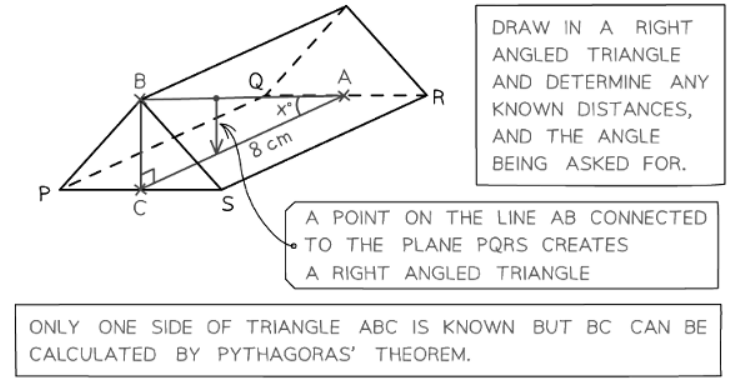
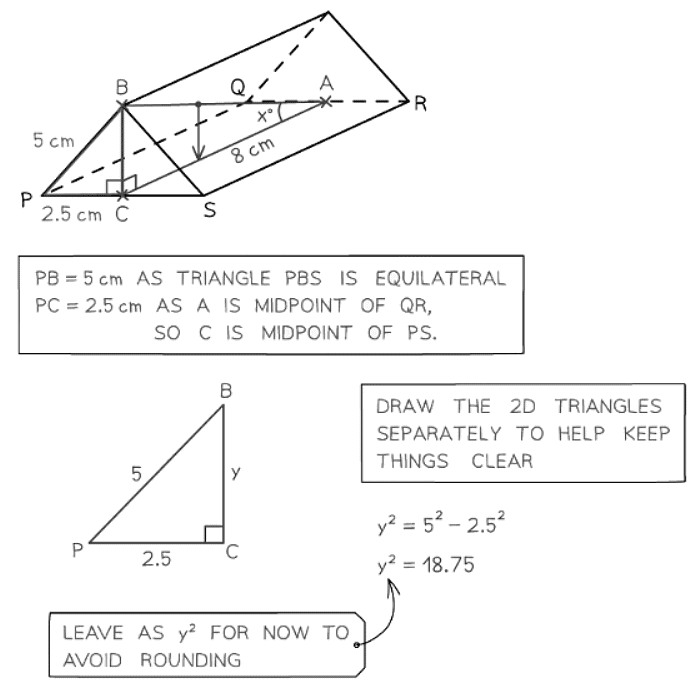
Question for 3D Pythagoras & TrigonometryTry yourself: How can Pythagoras' Theorem be used to find missing side lengths of a right-angled triangle?View Solution
The document 3D Pythagoras & Trigonometry | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
66 videos|674 docs|19 tests
|
FAQs on 3D Pythagoras & Trigonometry - Mathematics for GCSE/IGCSE - Class 10
| 1. How can I use Pythagoras' theorem in 3D geometry? |  |
Ans. In 3D geometry, Pythagoras' theorem can be used to find the length of the hypotenuse of a right-angled triangle in three-dimensional space. This can be applied to calculate distances, angles, and relationships between different points in 3D space.
| 2. How can trigonometry be applied in 3D geometry? |  |
Ans. Trigonometry can be applied in 3D geometry to calculate angles, distances, and relationships between different points or objects in three-dimensional space. Trigonometric functions such as sine, cosine, and tangent can be used to find unknown sides or angles in 3D shapes.
| 3. Can Pythagoras' theorem be used in non-right-angled triangles in 3D geometry? |  |
Ans. No, Pythagoras' theorem can only be applied to right-angled triangles in 3D geometry. For non-right-angled triangles, trigonometric functions or other geometric principles need to be used to find the lengths of sides or angles.
| 4. How can I determine the distance between two points in 3D space using trigonometry? |  |
Ans. To determine the distance between two points in 3D space using trigonometry, you can use the distance formula, which involves finding the differences in the x, y, and z coordinates of the two points and applying the Pythagorean theorem to calculate the distance.
| 5. What is the relationship between Pythagoras' theorem and trigonometry in 3D geometry? |  |
Ans. Pythagoras' theorem and trigonometry are closely related in 3D geometry, as both can be used to calculate distances, angles, and relationships between points in three-dimensional space. Pythagoras' theorem is often used to find the length of sides in right-angled triangles, while trigonometry can be used to solve more complex problems involving angles and distances in 3D shapes.
Related Searches















