Abnormal Molar Masses | Chemistry Class 12 - NEET PDF Download
ABNORMAL MOLAR MASS
Molecular masses of the solute can be easily determined with the help of colligative properties; relative lowering in vapour pressure, boiling point elevation, freezing point depression, and osmotic pressure easily. But, we derived the relation between the molecular mass of solute and colligative properties under some assumptions, which are:
- The solution is diluted that is, solvent is available in large amount in order to obey Raoult’s Law
- The solute neither went dissociation or association in the solution
So, how do we determine the molecular mass of solute in case the above assumptions are not valid? Basically, the abnormality is due to:
(i) Association of Solute Particles
- Some solute molecules start to associate inside the solution.
- This means now there are less number of solute particles in the solution.
- As colligative properties vary with solute particles in the solution, they will decrease along with the solute particles.
- As colligative properties are inversely proportional to the molecular mass of solute, we get a higher molar mass of the solute.
- For Example: Ethanoic acid or acetic acid ( CH3COOH) associate in solution to form a dimer due to hydrogen bonding.

Image 2: Ethanoic Acid dimer due to hydrogen bonding
(ii) Dissociation of Solute Particles
- Some solute molecules, generally electrolytes dissociate into two or more ions/particles when dissolved in a solution.
- This leads to increase in solute particles in the solution, thereby increase in colligative properties of solutions.
- As colligative properties and molecular mass of solute varies inversely, we get a lower molar mass of the solute.
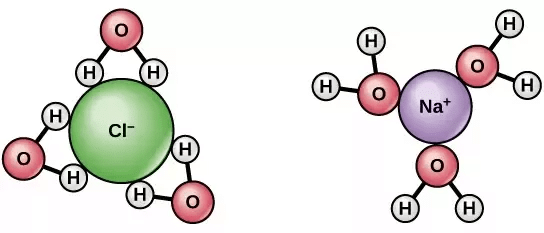 NaCl dissociate into two ions when dissolved in water
NaCl dissociate into two ions when dissolved in water
VAN’T HOFF FACTOR
To determine colligative properties for solutions which undergo association and dissociation, a Dutch physical chemist Jacobus Henricus van’t Hoff in the year 1880 introduced the concept of Van’t Hoff Factor i to sort out association and dissociation problem while calculating the molar mass of solute.
The Van’t Hoff factor is denoted by ‘i’ and is obtained when we divide normal mass with an abnormal mass of solute. Mathematically, it is represented in three forms:
i = Normal Molar Mass/Abnormal Molar Mass
i = Observed Colligative property/Calculated Colligative property
i = Total Number of Moles of Particles after Association/Dissociation / Total Number of Moles of Particles before Association / Dissociation
Thus, the value of i depends upon the state of solute in the solution.
Following cases become possible.
- When, i = 1, then the solute remains unaffected (i.e., normal) in solution.
- When, i > 1, then the solute undergoes dissociation in solution.
- When, i < 1, then the solute undergoes association in solution.
Thus, for
Potassium chloride (KCl) in aqueous solution, i is nearly equal to 2.
Barium chloride (BaCl2) in aqueous solution, i is nearly equal to 3.
Benzoic acid (C6H5COOH) in benzene, i is nearly equal to 0.5.
Acetic acid (CH3COOH) in benzene, i is nearly equal to 0.5.
CALCULATION OF I (VAN’T HOFF FACTOR)
First, we write an equation of the solute being associated or dissociated
CASE 1: WHEN SOLUTE UNDERGOES DISSOCIATION WHEN DISSOLVED IN SOLVENT
Degree of dissociation: It is defined as the number of moles dissociated over the initial number of moles taken.
Van’t Hoff factor = Total number of particles at equilibrium/Total initial number of particle
Let c moles per litre of an electrolyte AxBy be taken and let it dissociated as
AxBy →xAy+ + yBx–
t = 0 C 0 0
c (1 − α) xcα ycα At equilibrium
i = concentration or number of moles after dissociation/concentration or number of moles before dissociation
i =[c - cα + xcα + ycα ]/c
or i = [1 - α + xα + yα ]/1
= 1 + [(x + y)–1]α
Let x + y = n = number of particles formed after dissociation
i = 1 + (n – 1)α
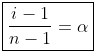
Degree of Association may be defined as the number of molecules associated per unit volume over initial concentration
i = Total number of particles or concentration after association/Total number of particles or concentration before association
Let n molecules of an electrolyte A undergo association
then, nA → An
C 0 t = 0
C – C · α C.α/n At. equilibrium
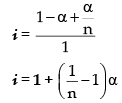
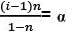 |
MODIFIED EQUATIONS FOR COLLIGATIVE PROPERTIES
For solutes which undergo dissociation or association in solutions, the equations for the colligative properties are modified by inserting the van'tHoff's factor in them as follows: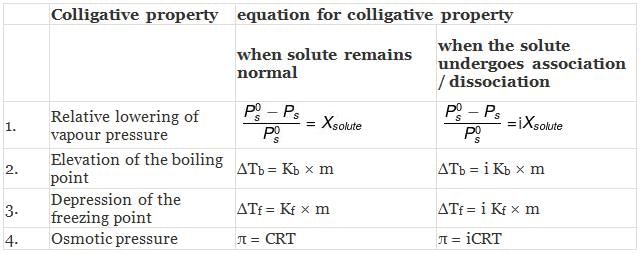
Example 1. Acetic acid (CH3COOH) associates in benzene to form double molecules. 1.65 g of acetic acid when dissolved in 100 g of benzene raised the boiling point by 0.36˚C. Calculate the Van't Hoff factor and the degree of association of acetic acid in benzene. (Kb = 2.57 K kg mol -1).
Solution.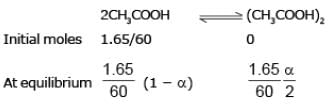
Total moles at equilibrium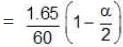
∆Tb = Kb × m,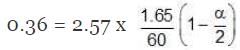
α = 0.981
Van't Hoff factor = no. of moles at equilibrium/Initial no. of moles
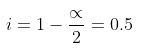
Example 2. Derive a relationship between Kb, Tb and ∆Hvap for a liquid.
Solution.
Let us consider a pure liquid. At its boiling point, Tb, its vapour pressure P˚ would be equal to the external pressure.
P˚ = Pext at temperature Tb.
Now let us consider a non-volatile solute dissolved in the liquid. When the solution reaches temperature Tb, the vapour pressure of the system, would be less than the external pressure. When the solution is heated further and it reaches its boiling Tb, the vapour pressure of the solution would be equal to Pext which is equal to the P˚ of the pure liquid at its boiling point. Since vapour pressure of a system are the Kp's for the respective equilibrium,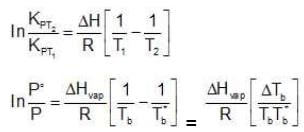
Assuming the solution to be highly dilute, Tb would be very close to Tb.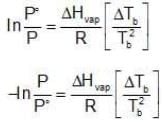
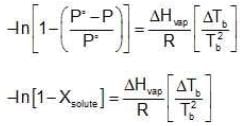
Since Xsolute is very small, we can make the approximation that in (1 - x) = -x (when x is very small).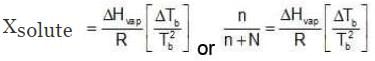
Ignoring n in comparison to N in the denominator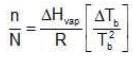
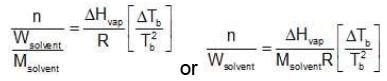
Multiplying by 1000 on both the sides, we get,
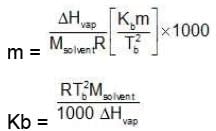
Similarly, Kf = 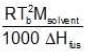
Example 3. To 500 cm3 of water, 3.0 × 10- 3 kg of acetic acid is added. If 23% of acetic acid is dissociated, what will be the depression in freezing point? Kf and density of water are 1.86 K kg-1 mol-1 and 0.997 g cm-3 respectively.
Solution. Molality of acetic acid

Total number of moles per kg of solvent = 0.1003 (1 + 0.23)
ΔTf = Kfm = 1.86 × 0.1003 × 1.23 = 0.23o C
Example. 4. At 300 K, the vapour pressure of an ideal solution containing one mole of A and 3 moles of B is 500 mm of Hg. At the same temperature, if one mole of B is added to this solution, the vapour pressure of the solution increases by 10 mm of Hg. Calculate the V.P. of A and B in their pure state.
Solution.
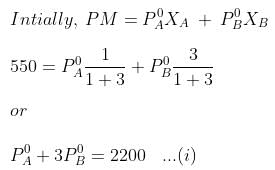
When, one mole of B is further added to it,
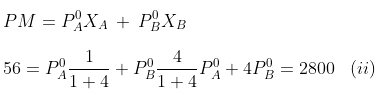
Solving equations (i) and (ii), we get
P°A= 440 mm, P°B= 600 mm
Example 5. A decinormal solution of NaCl exerts an osmotic pressure of 4.6 atm. at 300 K. Calculate its degree of dissociation. (R = 0.082 L atm. K-1mol-1).
Solution.
No. of moles of NaCl per litre of solution = 0.1
Osmotic pressure (p) = 4.6 atm., Temperature (T) = 300 K
Had NaCl not dissociated, then
p normal = CRT = 0.1 × 0.082 × 300 atm. = 2.46 atm.
But, pobs = 4.6 atm.
As per definition,
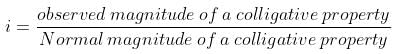
For the dissociation of an electrolyte producing n ions,
So, Percentage dissociation = 100 × a = 100 × 0.87 = 87%
Example 6. Vapour pressure of C6H6 and C7H8 mixture at 50˚C are given by: P = 179 XB 92, where XB is mole fraction of C6H6. Calculate (in mm):
(A) Vapour pressure of pure liquids.
(B) Vapour pressure of liquid mixture obtained by mixing 936 g C6H6 and 736 g toluene.
(C) If the vapours are removed and condensed into liquid and again brought to the temperature of 50˚C, what would be mole fraction of C6H6 in vapour state?
Solution.
(A) Given, P = 179XB + 92
For pure, C6H6, XB = 1
P°B= 179 + 92 = 271 mm
For pure C7H8, XB = 0
P°T= 179 x 0 + 92 = 92 mm
(B) Now PM = P°BXB + P°TXT
= 162.6 +36.8 = 199.4 mm
Moles of C6H6 = 936/78 = 12
Moles of C7H8 = 736/92 = 8
(C) Now mole fraction of C6H6 in vapour phase of initial mixture (X'T)
Moles fraction of C7H8 in vapour phase of initial mixture (X'L)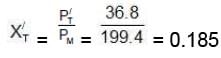
These vapours are taken out and condensed into liquid. The liquid is again brought to 50˚C to get again vapour-liquid equilibrium.
Thus, mole fraction of C6H6 in vapour phase of initial mixture
= Mole fraction of C6H6 in liquid phase on II mixture X'B
Similarly, mole fraction of C7H8 in vapour phase of initial mixture
= Mole fraction of C7H8 in liquid phase on II mixture X'T
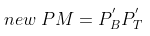 Therefore,
Therefore,

= 271 × 0.815 + 92 × 0.185 mm
= 220.865 + 17.02 = 237.885 mm
New mole fraction of C6H6 in vapour phase
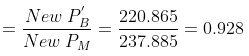
New mole fraction of C7H8 in vapour phase = 0.072.
Example 7. The freezing point depression of an HF (aq) solution with molality 0.10 m is -0.201˚C. What will be the Van’t Hoff factor? Take the value of Kf to be 1.86˚Cm-1
Solution.
HF (aq) → H+ + F-
We have Δ Tf = -0.201 C0 , m = 0.10 and Kf = 1.86 ˚Cm-1
The freezing point depression is Δ Tf = i Kfm
0.201 = i × 1.86 × 0.10
The value of Van’t Hoff factor will be 1.08
Example 8. A millimolar solution of potassium ferricyanide is 70% dissociated at 27°C. Find out the osmotic pressure of the solution.
Solution.
Given, concentration of solution = C = 1/1000 M = 10–3M
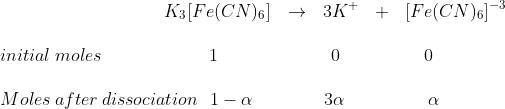
Where α = degree of dissociation = 70% = 70/100 = 0.7
Total moles of after dissociation = (1 – α) + 3α + α = 1+ 3α
∴ i = 1 + 3α/1
i = 1+3α = 1+(3 × 0.7) = 3.1
Since osmotic pressure
π = iCRT
∴ π = 3.1 × 10–3 × 0.0821 × 300
= 0.31 × 3 × 0.0821 atm = 0.07635 atm
TRY YOURSELF!
Q.1. A 0.5 percent aqueous solution of Potassium Chloride was found to freeze at 0.24°C. Calculate the Van't Hoff factor and degree of dissociation of the solute at this concentration (Kf for water is 1.86).
Ans. 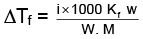
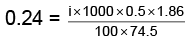
i = 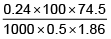
= 1.923; i = 1+(n–1)α
1.923 = 1+ (2–1)α ⇒ 1.923 = 1+ α
α = 1.923 – 1 = 0.923
or α = 0.923 or 92.3%
Q.2. If the apparent degree of ionization of KCl (KCl = 74.5 gm mol–1) in water at 290K is 0.86. Calculate the mass of KCl which must be made up to 1 dm3 of aqueous solution so as to produce the same osmotic pressure as the 4.0% solution of glucose at that temperature.,
Ans.
Due to ionization of KCl
From question, degree of ionization = a = 0.86
∴ i = 1+ 0.86 = 1.86
For Osmotic pressure of glucose,
For 4% glucose solution,
Weight of glucose = 40 gm,
Volume of solution = V = 1L = 1dm3
Molecular weight of glucose C6H12O6= m = 180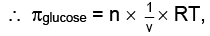 where πglucose = osmotic pressure of glucose
where πglucose = osmotic pressure of glucose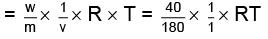
Similarly,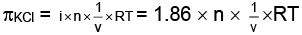
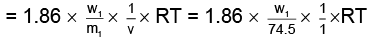
As both solutions are isotonic,
∴ πKCl = πglucose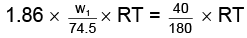
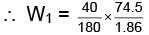
= 8.9 gm
|
108 videos|286 docs|123 tests
|
FAQs on Abnormal Molar Masses - Chemistry Class 12 - NEET
| 1. What are abnormal molar masses? |  |
| 2. How can isotopic variations affect molar masses? |  |
| 3. Can impurities in a substance affect its molar mass? |  |
| 4. What structural changes can lead to abnormal molar masses? |  |
| 5. How can abnormal molar masses impact chemical calculations? |  |

|
Explore Courses for NEET exam
|

|


















