Class 10 Maths Chapter 5 Question Answers - Arithmetic Progressions
Q1. How many two-digit numbers are divisible by 7?
Sol. Let 'n' two- digit numbers are divisible by 7.
So, the numbers are: 14, 21, 28, 35, 42, 49 ....................98.
This series form an A.P.
∴ a = 14,d = 7,and an = 98
Now, using an = a + (n - 1) d, we get
98 = 14 + (n - 1) 7
⇒ 98 = 14 + 7n - 7
⇒ 98 = 7 + 7n or 7n
= 98 - 7 = 91 ⇒ n = 91/7 = 13
Thus, required two-digit numbers is 13
Q2. If the numbers x - 2, 4x - 1 and 5x + 2 are in A.P. Find the value of x.
Sol. ∵ x - 2, 4x - 1 and 5x + 2 are in A.P.
∴ (4x - 1) - (x - 2) = (5x + 2) - (4x - 1)
⇒ 3x + 1 = x + 3
⇒ 2x = 2 ⇒ x = 1
Q3. Which term of the A.P. 4, 9, 14, ..... is 109?
Sol. Let 109 is the nth term,
∴ Using Tn = a + (n - 1) d, we have:
109 = 4 + (n - 1) 5
[∵ a = 4 and d = 9 - 4 = 5]
⇒ 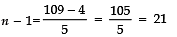
⇒ n = 21 + 1 = 22
Thus, the 22nd term is 109.
Q4. If a, (a - 2) and 3a are in A.P. then what is the value of a?
Sol. ∵ a, (a - 2) and 3a are in A.P.
∴ (a - 2) - a = 3a - (a - 2)
⇒ a - 2 - a = 3a - a + 2
⇒ - 2 = 2a + 2
⇒ 2a = - 2 - 2 = - 4
⇒ a = -4/2 = -2
Thus, the required value of a is - 2.
Q5. How many terms are there in the A.P.?
7, 10, 13, ....., 151
Sol. Here, a = 7, d = 10 - 7 = 3
Let there are n-terms.
∴ Tn = a + (n - 1) d
⇒ T51 = 7 + (n - 1) × 3
⇒ 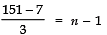
⇒ 144/3 = n − 1 ⇒ n = 48 + 1 = 49
i.e., n = 49
Q6. Which term of the A.P. 72, 63, 54, ..... is 0?
Sol. Here, a = 72
d = 63 - 72 = - 9
Let nth term of this A.P. be 0
∴ Tn = a + (n - 1) d
⇒ 72 + (n - 1) × (- 9) = 0
⇒ (n - 1) = -72/-9 = 8
⇒ n = 8 + 1 = 9
Thus the 9th term of the A.P. is 0.
Q7. The first term of an A.P. is 6 and its common difference is - 2. Find its 18th term.
Sol. Using Tn = a + (n - 1) d, we have:
T18 = 6 + (18 - 1) × (- 2)
= 6 + 17 × (- 2)
= 6 - 34 = - 28
Thus, the 18th term is - 28.
Q8. The 4th term of an A.P. is 14 and its 12th term 70. What is its first term
Sol. Let the first term = a
If ‘d’ is the common difference,
Then T4 = a + 3d = 14 ...(1)
And T12 = a + 11d = 70 ...(2)
Subtracting (1) from (2),
a + 11d - a - 3d = 70 - 14
⇒ 8d = 56 ⇒ d = 56/8 = 7
∴ From (1), a + 3 (7) = 14
⇒ a + 21 = 14
⇒ a = 14 - 21 = (- 7)
Thus, the first term is - 7.
Q9. Which term of A.P. 5, 2, - 1, - 4 ..... is - 40?
Sol. Here, a = 5
d = 2 - 5 = - 3
Let nth term be - 40
∴ Tn = a + (n - 1) d
⇒ - 40 = 5 + (n - 1) × (- 3)
⇒ n = 15 + 1 = 16 i.e.,
i.e., The 16th term of the A.P. is - 40.
Q10. What is the sum of all the natural numbers from 1 to 100?
Sol.
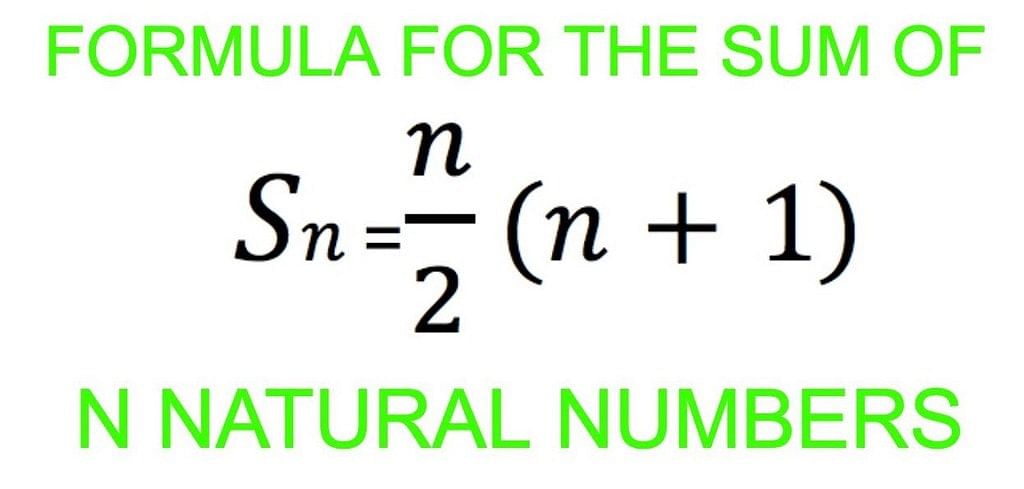
We have:
1, 2, 3, 4, ....., 100 are in an A.P. such that
a = 1 and l = 100
∴ Sn = n/2 [a + l]
⇒ S100 =100/2 [1 + 100]
= 50 × 101 = 5050.
Q11. For an A.P., the 8th term is 17 and the 14th term is 29. Find its common difference.
Sol. Let the common difference = d and first term = a
∴ T8 = a + 7d = 17 ...(1)
T14 = a + 13d = 29 ...(2)
Subtracting (1) from (2), we have:
a + 13d - a - 7d = 29 - 17
⇒ 6d = 12
⇒ d = 12/6 = 2
∴ The required common difference = 2.
Q12. If the first and last terms of an A.P. are 10 and - 10. How many terms are there? Given that d = - 1.
Sol. Let the required number of terms is n and
1st term a = 10
nth term Tn = - 10
Let common difference be d then using,
Tn = a + (n - 1) d, we have:
- 10 = 10 + (n - 1) × (- 1)
⇒ - 10 = 10 - n + 1
⇒ - n + 1 = - 10 - 10 = - 20
⇒ - n = - 20 - 1 = - 21
⇒ n = 21
13. The nth term of an A.P. is (3n - 2) find its first term.
Sol. ∵ Tn = 3n - 2
∴ T1 = 3 (1) - 2 = 3 - 2 = 1
⇒ First term = 1
Q14. The nth term of an A.P. is (2n - 3) find the common difference.
Sol. Here, Tn = 2n - 3
∴ T1 = 2 (1) - 3 = - 1
T2 = 2 (2) - 3 = 1
∴ d = T2 - T1 = 1 - (- 1) = 2
Thus the common difference is 2.
Q15. If the nth term of an A.P. is (7n - 5). Find its 100th term.
Sol. Here, Tn = 7n - 5
∴ T1 = 7 (1) - 5 = 2
T2 = 7 (2) - 5 = 9
∴ a = 2
and d = T2 - T1
= 9 - 2 = 7
Now T100 = 2 + (100 - 1) 7
[using Tn = a + (n - 1) d]
= 2 + 99 × 7
= 2 + 693 = 695.
Q16. Find the sum of first 12 terms of the A.P. 5, 8, 11, 14, ...... .
Sol. Here, a = 5
d = 8 - 5 = 3
n = 12
Using Sn = n/2 [2 (a) + (n - 1) d]
we have: S12 = 12/2 [2 (5) + (12 - 1) × 3]
= 6 [10 + 33]
= 6 × 43 = 258
Q17. Write the common difference of an A.P. whose nth term is 3n + 5.
Sol. Tn = 3n + 5
∴ T1 = 3 (1) + 5 = 8
T2 = 3 (2) + 5 = 11
⇒ d = T2 - T1
= 11 - 8 = 3
Thus, the common difference = 3.
Q18. Write the value of x for which x + 2, 2x, 2x + 3 are three consecutive terms of an A.P.
Sol. Here,
T1 = x + 2
T2 = 2x
T3 = 2x + 3
For an A.P., we have:
∴ 2x - (x + 2) = 2x + 3 - 2x
⇒ 2x - x - 2 = 2x + 3 - 2x
⇒ x - 2 = 3
⇒ x = 3 + 2 = 5
Thus, x = 5
Q19. What is the common difference of an A.P. whose nth term is 3 + 5n?
Sol. ∵ Tn = 3 + 5n
∴ T1 = 3 + 5 (1) = 8
And T2 = 3 + 5 (2) = 13
∵ d = T2 - T1
∴ d = 13 - 8 = 5
Thus, common difference = 5.
Q20. For what value of k, are the numbers x, (2x + k) and (3x + 6) three consecutive terms of an A.P.?
Sol. Here, T1 = x, T2 = (2x + k) and T3 = (3x + 6)
For an A.P., we have
T2 - T1 = T3 - T2
i.e., 2x + k - x = 3x + 6 - (2x + k)
⇒ x + k = 3x + 6 - 2x - k
⇒ x + k = x + 6 - k
⇒ k + k = x + 6 - x
⇒ 2k = 6
⇒ k = 6/2 = 3
Q21. For what value of k, will k + 9, 2k - 1 and 2k + 7 are consecutive terms of an A.P.?
Sol. ∵ T1 = k + 9, T2 = 2k - 1 and T3 = 2k + 7
For an A.P., T2 - T1 = T3 - T2
∴ (2k - 1) - (k + 9) = (2k + 7) - (2k - 1)
⇒ 2k - 1 - k - 9 = 2k + 7 - 2k + 1
⇒ k - 10 = 8
⇒ k = 8 + 10
⇒ k = 18
Q22. If 4/5, a, 2 are three consecutive terms of an A.P., then find the value of a?
Sol. Here,
T1 = 4/5
T2 = a
T3 = 2
∵ For an A.P.,
T2 - T1 = T3 - T2
∴ 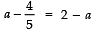
⇒ 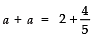
⇒ 2a = 14/5
⇒ 
Thus, a = 7/5
Q23. For what value of p are 2p - 1, 7 and 3p three consecutive terms of an A.P.?
Sol. Here,
T1 = 2p - 1
T2 = 7
T3 = 3p
∵ For an A.P., we have:
T2 - T1 = T3 - T2
⇒ 7 - (2p - 1) = 3p - 7
⇒ 7 - 2p + 1 = 3p - 7
⇒ - 2p - 3p = - 7 - 1 - 7
⇒ - 5p = - 15
⇒ p = -15/-5 = 3
Thus, p = 3
Q24. For what value of p are 2p + 1, 13 and 5p - 3 three consecutive terms of an A.P.?
Sol. Here,
T1 = 2p + 1
T2 = 13
T3 = 5p - 3
For an A.P., we have:
T2 - T1 = T3 - T2
⇒ 13 - (2p + 1) = 5p - 3 - 13
⇒ 13 - 2p - 1 = 5p - 16
⇒ - 2p + 12 = 5p - 16
⇒ - 2p - 5p = - 16 - 12 = - 28
⇒ - 7p = - 28
⇒ 
∴ p = 4
Q25. The nth term of an A.P. is 7 - 4n. Find its common difference.
Sol. ∵ Tn = 7 - 4n
∴ T1 = 7 - 4 (1) = 3
T2 = 7 - 4 (2) = - 1
∴ d = T2 - T1
= (- 1) - 3 = - 4
Thus, common difference = - 4
Q26. The nth term of an A.P. is 6n + 2. Find the common difference.
Sol. Here, Tn = 6n + 2
∴ T1 = 6 (1) + 2 = 8
T2 = 6 (2) + 2 = 14
⇒ d = T2 - T1 = 14 - 8 = 6
∴ Common difference = 6.
Q27. Write the next term of the A.P. √8, √18 √32 ......
Sol.
Here, 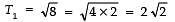

∴ 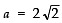
Now, d = T2 − T1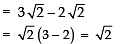
∴ T4 = a + 3d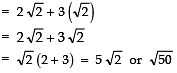
Thus, the next term of the A.P. is 5√2 or 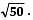
Q28. The first term of an A.P. is p and its common difference is q. Find the 10th term.
Sol. Here, a = p and d = q
∵ Tn = a + (n - 1) d
∴ T10 = p + (10 - 1) q
= p + 9q
Thus, the 10th term is p + 9q.
Q29. (a) Find the next term of the A.P. 
(b) Find the tenth term of the sequence 
Sol. (a) Here, 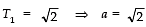
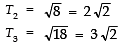
Now, d = T2 − T1
Now, using Tn = a + (n - 1) × d, we have
T4 = a + 3d
Thus, the next term = √32.
(b) Here, T10 = a + 9d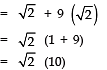

Q30. Which term of the A.P.:
21, 18, 15, ..... is zero?
Sol. Here, a = 21
d = 18 - 21 = - 3
Since Tn = a + (n - 1) d
⇒ 0 = 21 + (n - 1) × (- 3)
⇒ - 3 (n - 1) = - 21
⇒ (n - 1) = -21/-3 = 7
⇒ n = 7 + 1 = 8
Thus, the 8th term of this A.P. will be 0.
Q31. Which term of the A.P.:
14, 11, 8, ..... is - 1?
Sol. Here, a = 14
d = 11 - 14 = - 3
Let the nth term be (- 1)
∴ Using Tn = a + (n - 1) d, we get
- 1 = 11 + (n - 1) × (- 3)
⇒ - 1 - 14 = - 3 (n - 1)
⇒ - 15 = - 3 (n - 1)
∴ n - 1 = -15/-3 = 5
⇒ n = 5 + 1 = 6
Thus, -1 is the 6th term of the A.P.
Q32. The value of the middlemost term (s) of the AP : –11, –7, –3, ...49.
Sol. ∵ a = –11, an = 49 and d = (–7) – (–11) = 4
∴ an = a + (n – 1)d
⇒ 49 = –11 + (n – 1) × 4
⇒ n = 16
Since, n is an even number
∴ There will be two middle terms, which are: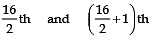
or 8th and 9th
Now, a8 = a + (8 – 1)d
= –11 + 7 × 4 = 17
a9 = a + (9 – 1)d
= –11 + 8 × 4 = 21
Thus, the values of the two middlemost terms are 17 and 21.
FAQs on Class 10 Maths Chapter 5 Question Answers - Arithmetic Progressions
| 1. What is an arithmetic progression? |  |
| 2. How is the nth term of an arithmetic progression calculated? |  |
| 3. Can an arithmetic progression have negative terms? |  |
| 4. How can we find the sum of the first n terms of an arithmetic progression? |  |
| 5. Can the common difference of an arithmetic progression be zero? |  |





















